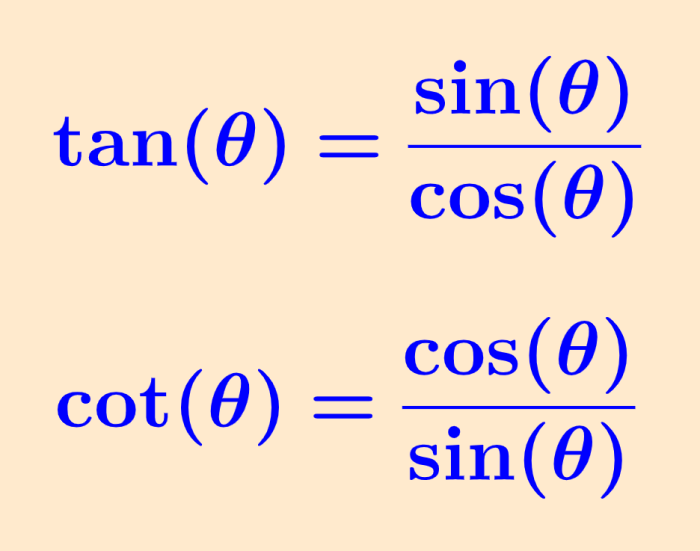Quotient identities are trigonometric identities that are written as fractions of the sine and cosine functions. The tangent forms a quotient identity and can be written as the sine of the angle divided by the cosine. Similarly, the cotangent can be written as the cosine of the angle divided by the sine.
Here, we will learn about the origin of the quotient identities. Then, we will use these identities to solve some practice problems.
What are the quotient identities?
The quotient identities are the trigonometric identities written in terms of the fundamental trigonometric functions, sine, and cosine.
Let’s consider the sine, cosine, and tangent functions. If we define these functions in a right triangle, we have the following:
$latex \sin(\theta)=\frac{O}{H}$
$latex \cos(\theta)=\frac{A}{H}$
$latex \tan(\theta)=\frac{O}{A}$
where, O is the side opposite the angle, A is the side adjacent to the angle, and H is the hypotenuse of the triangle.
Given these definitions, we can show that $latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$, as long as $latex \cos(\theta)\neq 0$:
$latex \frac{\sin(\theta)}{\cos(\theta)}=\frac{\frac{O}{H}}{\frac{A}{H}}$
$latex =\frac{O}{A}=\tan(\theta)$
We have verified that we can write the tangent function as the sine of the angle divided by the cosine. Also, since the cotangent is the reciprocal identity of the tangent. We can write the cotangent as the cosine of the angle divided by the sine. Therefore, we have the two quotient identities:
| $latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$ $latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$ |
Quotient identities – Examples with answers
The trigonometric quotient identities are used to solve the following examples. Each example has its respective solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
If we have the values $latex \cos (\theta) = \frac{3}{11}$ and $latex \sin (\theta) = \frac{5}{11}$, what is the value of $latex \tan (\theta)$?
Solution
We use the identity of the quotient of the tangent to solve this problem. Therefore, we have to divide the value of the sine by the value of the cosine:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \tan(\theta)=\frac{\frac{5}{11}}{\frac{3}{11}}$
$latex \tan(\theta)=\frac{5}{3}$
EXAMPLE 2
Show that the identity $latex \cot (\theta) = \frac{\cos (\theta)}{\sin(\theta)}$ is true.
Solution
To show that the given identity is true, we can use the definitions of sine, cosine, and tangent in terms of a right triangle. Therefore, we know that the cosine is defined as the adjacent side (A) over the hypotenuse (H) and the sine is defined as the opposite side (O) over the hypotenuse, so we have:
$latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$
$latex \cot(\theta)=\frac{\frac{A}{H}}{\frac{O}{H}}$
$latex \cot(\theta)=\frac{A}{O}$
We have that the cotangent is equal to the adjacent side divided by the opposite side, which is correct since the cotangent is the reciprocal function of the tangent.
EXAMPLE 3
We have the values $latex \cos (\theta) = \frac{5}{7}$ and $latex \sin (\theta) = \frac{2}{7}$. Determine the value of $latex \cot(\theta)$.
Solution
In this case, we have the cotangent function, so we know that we can calculate its value by dividing the value of the cosine by the value of the sine. Therefore, we have:
$latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$
$latex \cot(\theta)=\frac{\frac{5}{7}}{\frac{2}{7}}$
$latex \cot(\theta)=\frac{5}{2}$
EXAMPLE 4
What is the value of $latex \sin (\theta)$ if we have the values $latex \tan (\theta) = \frac{12}{5}$ and $latex \cos(\theta) = \frac{5}{9}$?
Solution
Again we have the tangent function, however, in this case we have to find the value of the sine. We use the identity of the quotient of the tangent and solve for the sine:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \frac{12}{5}=\frac{\sin(\theta)}{\frac{5}{9}}$
$latex \sin(\theta)=(\frac{12}{5})(\frac{5}{9})$
$latex \sin(\theta)=\frac{12}{9}=\frac{4}{3}$
Quotient identities – Practice problems
Solve the following problems applying what you have learned about quotient identities. Select an answer and check it to see if you got the correct solution.
See also
Interested in learning more about trigonometric identities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
