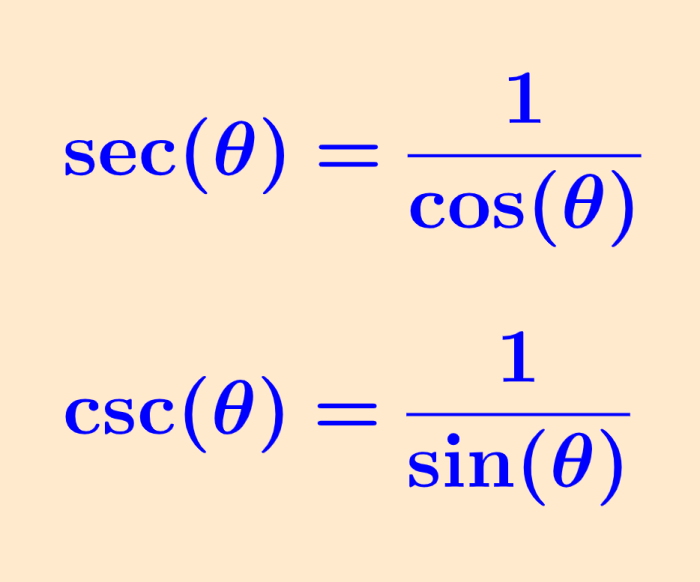We have already become familiar with the trigonometric functions of sine, cosine, and tangent. These functions are written as fractions relating to the sides of a right triangle. We also know that the reciprocal of a fraction is equal to the original fraction with its numerator and denominator swapped. Then, the reciprocal identities are formed by interchanging the numerator and denominator of cosine, sine, and tangent to form the secant, cosecant, and cotangent functions respectively.
Here, we will learn more details of the trigonometric reciprocal identities and use them to solve some practice problems.
What are the reciprocal identities?
The reciprocal identities are trigonometric identities that are defined with respect to the fundamental trigonometric functions, sine, cosine, and tangent. A reciprocal of the fraction $latex \frac{a}{b}$ is the fraction $latex \frac{b}{a}$. This means that we find the reciprocal of a fraction by swapping the positions of the numerator and denominator.
Let’s consider the sine function for the angle θ. This function is defined as the opposite side divided by the hypotenuse. Therefore, we have $latex \sin(\theta) = \frac{O}{H}$. The cosecant function is defined as $latex \csc (\theta)=\frac{H}{O}$. This means that these two functions are reciprocal.
Therefore, the value of the sine of an angle is always equal to the reciprocal of the value of the cosecant and vice versa. For example, if we have $latex \sin(\theta) = \frac{1}{2}$, then we also have $latex \csc(\theta) = 2$.
Similarly, the cosine function and the secant function are reciprocal, and the tangent function and the cotangent function are also reciprocal. Therefore, we have the following reciprocal identities:
| $latex \csc(\theta)=\frac{1}{\sin(\theta)}$ $latex \sec(\theta)=\frac{1}{\cos(\theta)}$ $latex \cot(\theta)=\frac{1}{\tan(\theta)}$ |
Law of cosines – Examples with answers
The reciprocal identities are used to solve the following examples. Each of the examples has its respective solution, but it is recommended that you try to solve the problems yourself.
EXAMPLE 1
If we have $latex \cos (\theta) = 0.2$, what is the value of $latex \sec (\theta)$?
Solution
The cosine and secant functions are reciprocal, so we know that we can “flip” the fraction of the cosine value to find the value of the secant. To facilitate this, we write the cosine as a fraction:
$latex \cos(\theta)=0.2=\frac{2}{10}$
Therefore, we have:
$latex \sec(\theta)=\frac{1}{\cos(\theta)}$
$latex =\frac{10}{2}$
EXAMPLE 2
If we have $latex \cot (\theta) = \frac{5}{3}$, what is the value of $latex \tan (\theta)$?
Solution
The tangent and cotangent functions are reciprocal. Therefore, we can find the value of the tangent by “flipping” the fraction of the value of the cotangent. Thus, we have:
$latex \cot(\theta)=\frac{5}{3}$
⇒ $latex \tan(\theta)=\frac{3}{5}$
EXAMPLE 3
Verify the identity $latex \tan(\theta)+\cot(\theta)=\sec(\theta)\csc(\theta)$.
Solution
We can rewrite everything in terms of sine and cosine, remembering that the tangent function is equal to sine divided by cosine. Therefore, we have:
$latex \tan(\theta)+\cot(\theta)=\sec(\theta)\csc(\theta)$
$latex \frac{\sin(\theta)}{\cos(\theta)}+\frac{\cos(\theta)}{\sin(\theta)}=\frac{1}{\cos(\theta)}\cdot \frac{1}{\sin(\theta)}$
We can add the fractions on the left by forming the common denominator $latex \cos(\theta)\sin(\theta)$:
$latex \frac{\sin(\theta)}{\cos(\theta)}+\frac{\cos(\theta)}{\sin(\theta)}=\frac{1}{\cos(\theta)}\cdot \frac{1}{\sin(\theta)}$
$latex \frac{{{\sin}^2}(\theta)+{{\cos}^2}(\theta)}{\sin(\theta)\cos(\theta)}=\frac{1}{\cos(\theta)}\cdot \frac{1}{\sin(\theta)}$
$latex \frac{1}{\sin(\theta)\cos(\theta)}=\frac{1}{\cos(\theta)}\cdot \frac{1}{\sin(\theta)}$
In the last step, we use the main Pythagorean identity $latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$. We see that we got the same expression on both sides. This means that the given identity is true.
Reciprocal identities – Practice problems
Solve the following practice problems using reciprocal identities. If you need help with this, see the solved examples above.
See also
Interested in learning more about trigonometric identities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
