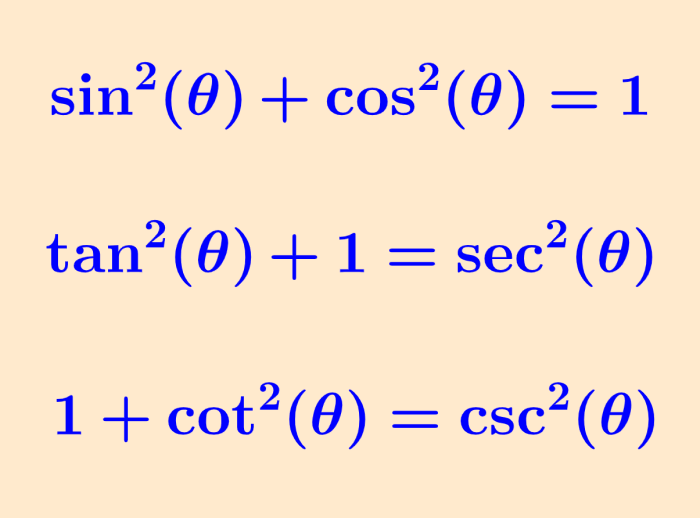Pythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem. Pythagorean identities are useful for simplifying trigonometric expressions. These identities are especially used to write expressions such as a sine or cosine function as double angle formulas.
Here, we will learn about the Pythagorean identities and we will learn to derive them from the Pythagorean theorem. Then, we will look at some practice problems where we will apply these identities.
What are the Pythagorean identities?
Pythagorean identities are equations that contain trigonometric functions, which are true for all substituted values in the variables. Trigonometric identities are especially useful for simplifying trigonometric expressions. The trigonometric identities are derived from the Pythagorean theorem:
| $latex {{\sin}^2} (\theta)+{{\cos}^2} (\theta)=1$ |
This is the most important Pythagorean identity. This identity is true for all values of θ. Using this first identity, we can create two additional Pythagorean identities:
| $latex {{\tan}^2} (\theta)+1={{\sec}^2} (\theta)$ $latex 1+{{\cot}^2} (\theta)={{\csc}^2} (\theta)$ |
where “tan” represents the tangent function, “sec” represents the secant function, “cot” represents the cotangent function, and “csc” represents the cosecant function.
How to derive the Pythagorean identities?
We can derive the Pythagorean identities using the unit circle. Recall that the unit circle is a circle with a radius of 1. In this triangle, the x-coordinates are represented by $latex \cos (\theta)$ and the y-coordinates are represented by $latex \sin (\theta)$ as shown in the following diagram:
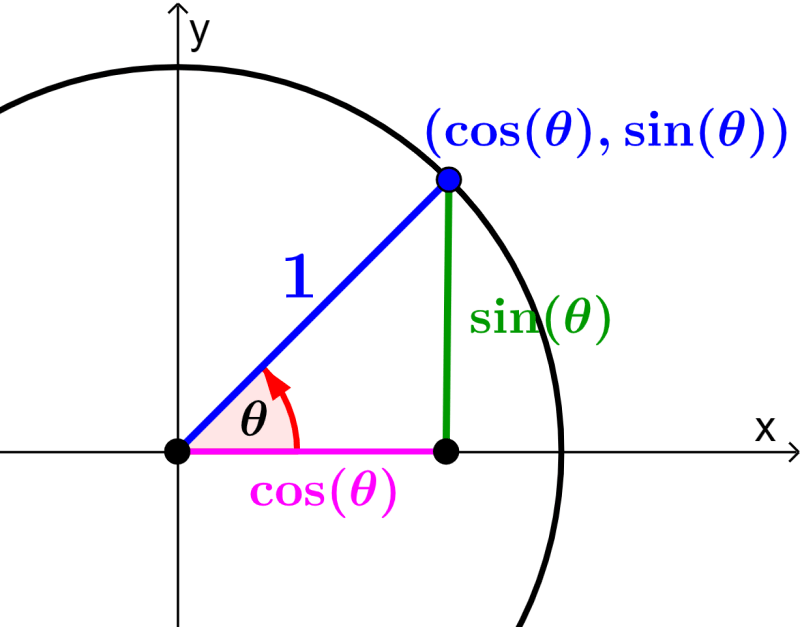
We see that the legs of the right triangle in the unit circle have the values of $latex \sin (\theta)$ and $latex \cos(\theta)$. Also, the hypotenuse of the triangle is the radius of the circle, which is equal to 1. Therefore, using the Pythagorean theorem, we have:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
This is the main Pythagorean identity. Using this identity, we can derive two additional identities.
We start with the first Pythagorean identity:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
We divide each term by $latex {{\cos}^2}(\theta$:
$$\frac{{{\sin}^2}(\theta)}{{{\cos}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\cos}^2}(\theta)}=\frac{1}{{{\cos}^2}(\theta)}$$
Now, we know that we have $latex \frac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)$ y $latex \frac{1}{\cos(\theta)}=\sec(\theta)$. Therefore, by substituting and simplifying, we have:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)$
If we divide by a different value, we can find the third Pythagorean identity. We start with the first Pythagorean identity:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
We divide each term by $latex {{\sin}^2}(\theta)$:
$$\frac{{{\sin}^2}(\theta)}{{{\sin}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\sin}^2}(\theta)}=\frac{1}{{{\sin}^2}(\theta)}$$
Now, we can use the relations $latex \frac{\cos(\theta)}{\sin(\theta)}=\cot(\theta)$ y $latex \frac{1}{\sin(\theta)}=\csc(\theta)$. Therefore, by substituting and simplifying, we have:
$latex 1+{{\cot}^2}(\theta)={{\csc}^2}(\theta)$
Examples with answers of the Pythagorean identities
The Pythagorean identities derived above are used to solve the following exercises. Try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
Simplify the expression $latex \sin(x){{\cos}^2}(x) – \sin(x)$ using the Pythagorean identities.
Solution
This expression contains the sine and the cosine, so we can use the identity $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$. Therefore, we start by factoring to the given expression:
$$\sin(x){{\cos}^2}(x)-\sin(x)=\sin(x)({{\cos}^2}(x)-1)$$
We can rewrite the identity $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$ in the following way: $latex {{\cos}^2}(x)-1=-{{\sin}^2}(x)$. Thus, by substituting this identity, we have:
$$\sin(x)({{\cos}^2}(x)-1)=\sin(x)(-{{\sin}^2}(x))$$
$latex ={{\sin}^3}(x)$
EXAMPLE 2
Express the trigonometric expression $latex {{\csc}^2}(x) – \cot(x) -3$ in factored form.
Solution
We can use the Pythagorean identity $latex 1+{{\cot}^2}(x)={{\csc}^2}(x)$. Therefore, substituting, we have:
$latex {{\csc}^2}(x)-\cot(x)-3$
$latex =1+\cot^2(x)-\cot(x)-3$
$latex =\cot^2(x)-\cot(x)-2$
$latex =(\cot(x)-2)(\cot(x)+1)$
EXAMPLE 3
Simplify the trigonometric expression $$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
Solution
In this case, we have to recognize that $latex \sec(x)=\frac{1}{\cos(x)}$ and $latex \csc(x)=\frac{1}{\sin(x)}$. Using this, we have:
$$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
$$=({{\sec}^2}(x))(1-{{\sin}^2}(x))-({{\sin}^2}(x)+{{\cos}^2}(x))$$
Now, we use the main Pythagorean identity and we have:
$latex =({{\sec}^2}(x))({{\cos}^2}(x))-(1)$
$latex =1-1$
$latex =0$
EXAMPLE 4
If we have $latex \tan(\theta)=\frac{1}{3}$, what is the value of $latex \frac{1}{{{\sin}^2}(\theta)}+\frac{1}{{{\cos}^2}(\theta)}$?
Solution
We can use the second and third Pythagorean identities. In addition, we remember that the secant is equal to $latex \frac{1}{\cos(\theta)}$ and the cosecant is equal to $latex \frac{1}{\sin(\theta)}$. Using this, we have:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)=\frac{1}{{{\cos}^2}(\theta)}$
$latex {{\cot}^2}(\theta)+1={{\csc}^2}(\theta)=\frac{1}{{{\sin}^2}(\theta)}$
Substituting this in the original expression, we have:
$latex \frac{1}{{{\sin}^2}(\theta)}+\frac{1}{{{\cos}^2}(\theta)}$
$latex ={{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
Now, we know that $latex \tan(\theta)=\frac{1}{3}$. Also, since the cotangent is the reciprocal of the tangent, this means that $latex \cot(\theta)=3$. Using these values, we have:
$latex {{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
$latex ={{3}^2}+1+(\frac{1}{3})^2+1$
$latex =\frac{100}{9}$
See also
Interested in learning more about trigonometric identities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
