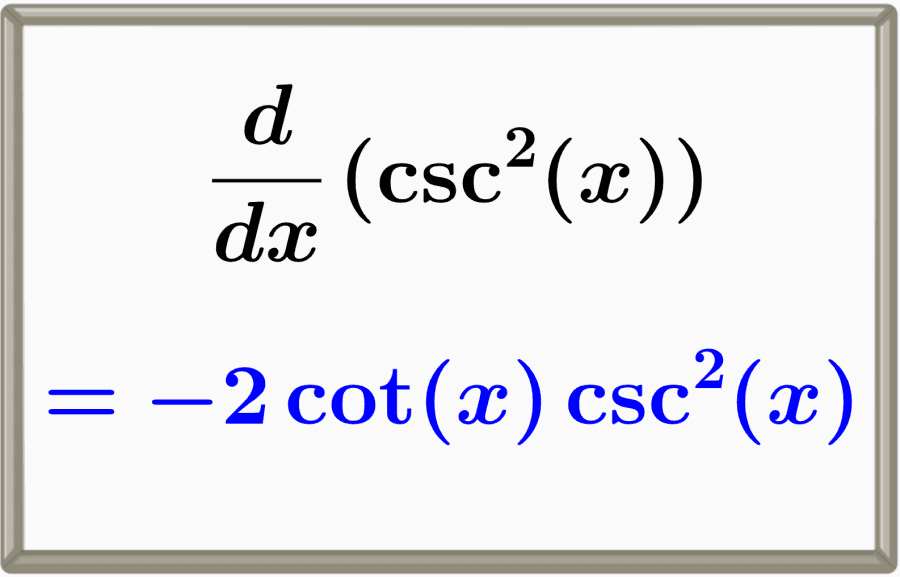The derivative of cosecant squared is equal to minus two contingent times cosecant squared, -2cot(x)csc2(x). We can find this derivative by using the chain rule and the derivatives of the fundamental trigonometric functions.
Here, we will look at a demonstration of this derivative, the graphical comparison of the cosecant squared and its derivative, and some examples.
Proof of The Derivative of Cosecant Squared Function with the use of Chain Rule
As a prerequisite, please review the chain rule formula and its proof by looking at the article: Chain Rule of derivatives. Similarly, you can review the proof of the derivative of cosecant function by visiting this article: Derivative of Cosecant, csc(x).
Please be reminded that
$latex \csc^{2}{(x)} \neq \csc{(x^2)}$
This is a composite cosecant function, so it can be differentiated using the chain rule. Therefore, we start with the function:
$latex F(x) = \csc^{2}{(x)}$
We can identify the two functions that make up F(x). One function is raised to a power of two and the other is a trigonometric function of cosecant.
If we rewrite the function as follows, we can see this more clearly:
$latex F(x) = \csc^{2}{(x)}$
$latex F(x) = (\csc{(x)})^2$
Now it is clear that the power function is the external function, while the cosecant function is the internal function. We can configure the outer function as follows:
$latex f(u) = u^2$
where
$latex u = \csc{(x)}$
The trigonometric cosecant function, as the inner function of f(u), will be denoted as g(x).
$latex f(u) = f(g(x))$
$latex u = g(x)$
$latex g(x) = \csc{(x)}$
Deriving the outer function f(u) using the power rule in terms of u, we have
$latex f(u) = u^2$
$latex f'(u) = 2u$
Deriving the inner function g(x) using the derivative formula of trigonometric function cosecant in terms of x, we have
$latex g(x) = \csc{(x)}$
$latex g'(x) = -\csc{(x)}\cot{(x)}$
Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have
$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$
$latex \frac{dy}{dx} = (2u) \cdot (-\csc{(x)}\cot{(x)})$
Substituting u into f'(u), we have
$latex \frac{dy}{dx} = (2(\csc{(x)})) \cdot (-\csc{(x)}\cot{(x)})$
$latex \frac{dy}{dx} = -(2(\csc{(x)})) \cdot (\csc{(x)}\cot{(x)})$
$latex \frac{dy}{dx} = -2\csc^{2}{(x)} \cdot \cot{(x)}$
which brings us to the derivative formula of cosecant squared x
$latex \frac{d}{dx} \csc^{2}{(x)} = -2\cot{(x)}\csc^{2}{(x)}$
Relationship between the derivative of cosecant squared and cotangent squared
You may wonder why
$latex \csc^{2}{(x)}$
and
$latex \cot^{2}{(x)}$
have similar derivatives.
According to the Pythagorean formula for cosecants and cotangents,
$latex \csc^{2}{(x)} = 1 + \cot^{2}{(x)}$
If we try to derive both sides of the equation, we have
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(1) + \frac{d}{dx}(\cot^{2}{(x)})$
Evaluating the derivative of the first term in the right-hand-side of the equation, where the derivative is zero, we have
$latex \frac{d}{dx} (\csc^{2}{(x)}) = 0 + \frac{d}{dx}(\cot^{2}{(x)})$
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(\cot^{2}{(x)})$
This is why both the cosecant squared and the cotangent squared have the same derivative, because of the Pythagorean formula for cosecants and cotangents.
Graph of Cosecant Squared x VS. The Derivative of Cosecant Squared x
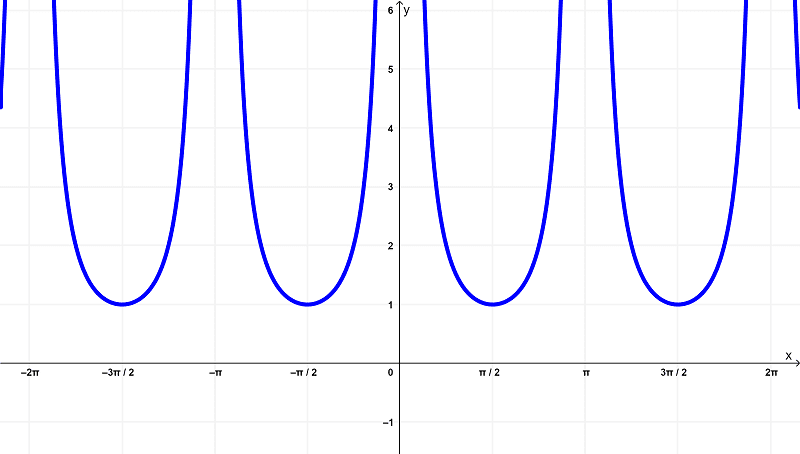
Given the function
$latex f(x) = \csc^{2}{(x)}$
it is graphed as
As we already know, deriving $latex f(x) = \csc^{2}{(x)}$ is
$latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$
which is graphed as
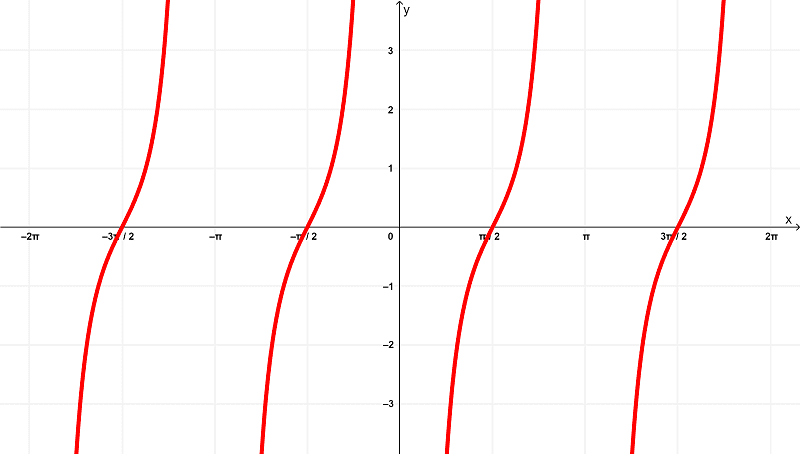
Illustrating both graphs in one, we have

By examining the differences between these functions basing on the graphs above, you can see that the original function $latex f(x) = \csc^{2}{(x)}$ has a domain of
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
within the finite intervals of
$latex (-2\pi,2\pi)$
and lies within the range of
$latex [1,\infty)$
whereas the derivative $latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$ has a domain of
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
within the finite intervals of
$latex (-2\pi,2\pi)$
and lies within the range of
$latex (-\infty,\infty)$
Examples
In the following examples, we can see how to derive a compound cosecant squared function.
EXAMPLE 1
Determine the derivative of the function $latex f(x) = \csc^2(15x)$.
Solution
This is a composite cosecant squared function, so the use of the chain rule is required to find its derivative.
Therefore, let’s use $latex u=15x$ as the inner function, so we have $latex f(u)=\csc^2(u)$. Using the chain rule, this gives us:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-2\cot(u)\csc^2(u) \times 15$$
We just have to substitute $latex u=15x$ back into the function and we have:
$$\frac{dy}{dx}=-30\cot(15x)\csc^2(15x)$$
EXAMPLE 2
Find the derivative of the function $latex F(x) = \csc^2(6x^3-8x)$
Solution
In this case, the inner function is $latex 6x^3-8x$, which allows us to write $latex f (u) = \csc^2(u)$.
Then, we can find the derivative of the external function
$$\frac{d}{du} ( \csc^2(u) ) = -2\cot(u)\csc^2(u)$$
Calculating the derivative of $latex g(x)=u=6x^3-8x$, we have:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(6x^3-8x)$$
$$\frac{d}{dx}(g(x)) = 18x^2-8$$
Multiplying the derivative of the external function $latex f(u)$ by the derivative of the internal function $latex g(x)$, we have:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -2\cot(u)\csc^2(u) \cdot (18x^2-8)$$
Finally, we apply the substitution $latex u=6x^3-8x$ and simplify:
$$\frac{dy}{dx} = -2\cot(6x^3-8x)\csc^2(6x^3-8x) \cdot (18x^2-8)$$
$$\frac{dy}{dx} = -(36x^2-16)\cot(6x^3-8x)\csc^2(6x^3-8x)$$
Practice of derivatives of cosecant squared functions


See also
Interested in learning more about the derivatives of trigonometric functions squared? Take a look at these pages:
- Derivative of Cosine Squared, cos^2(x) with Proof and Graphs
- Derivative of Sine Squared, sin^2(x) with Proof and Graphs
- Derivative of Tangent Squared, tan^2(x) with Proof and Graphs
- Derivative of Secant Squared, sec^2(x) with Proof and Graphs
- Derivative of Cotangent Squared, cot^2(x) with Proof and Graphs