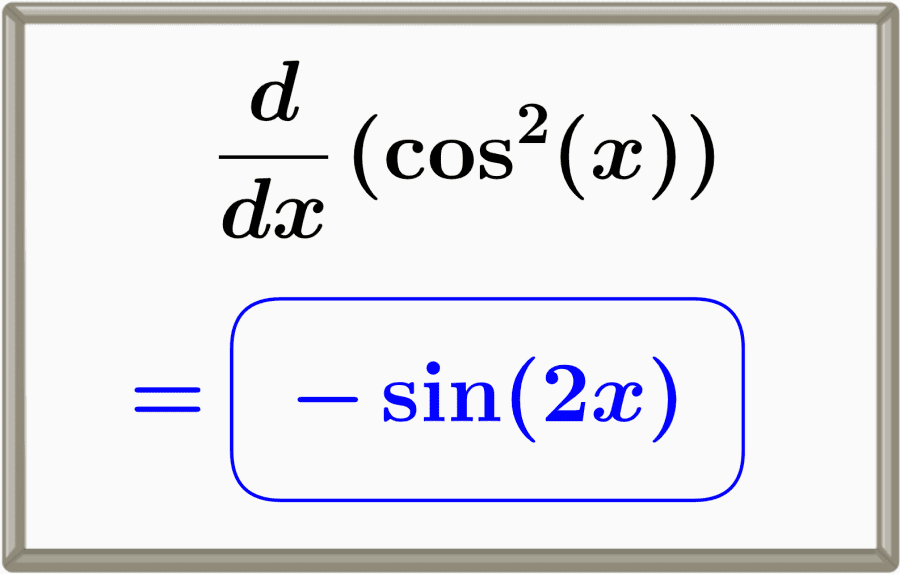Derivative of Cosine Squared, cos^2(x) with Proof and Graphs

Proof of The Derivative of Cosine Squared Function Using Chain Rule

If you need it, you are encouraged to review the chain rule formula, as a prerequisite of this topic, by visiting this link: Chain Rule of derivatives. Likewise, you may visit this another link for the proof of the derivative of cosine function: Derivative of Cosine, cos(x).

Please take note that

$latex \cos^{2}{(x)} \neq \cos{(x^2)}$

Because it is a composite function, the chain rule formula is used to find the derivative of the cosine squared function.

Therefore, we start with the function

$latex F(x) = \cos^{2}{(x)}$

We can identify the two functions that make up F(x). There is a power function and a trigonometric function in this scenario.

For easier representation, we can rewrite our given as

$latex F(x) = \cos^{2}{(x)}$

$latex F(x) = (\cos{(x)})^2$

It is now very clear that the given power function is the outer function, while the cosine function is the inner function. We can set the outer function as

$latex f(u) = u^2$

where

$latex u = \cos{(x)}$

Setting the trigonometric cosine function as the inner function of f(u) by denoting it as g(x), we have

$latex f(u) = f(g(x))$

$latex u = g(x)$

$latex g(x) = \cos{(x)}$

Deriving the outer function f(u) using the power rule in terms of u, we have

$latex f(u) = u^2$

$latex f'(u) = 2u$

Deriving the inner function g(x) using the derivative formula of trigonometric function cosine in terms of x, we have

$latex g(x) = \cos{(x)}$

$latex g'(x) = -\sin{(x)}$

Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have

$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$

$latex \frac{dy}{dx} = (2u) \cdot (-\sin{(x)})$

Substituting u into f'(u), we have

$latex \frac{dy}{dx} = (2(\cos{(x)})) \cdot (-\sin{(x)})$

$latex \frac{dy}{dx} = -2\cos{(x)}\sin{(x)}$

$latex \frac{dy}{dx} = -2\sin{(x)}\cos{(x)}$

Applying the double angle identities, we have

$latex \frac{dy}{dx} = -(2\sin{(x)}\cos{(x)})$

$latex \frac{dy}{dx} = -(\sin{(2x)})$

This gets us to the cosine squared x derivative formula.

$latex \frac{d}{dx} \cos^{2}{(x)} = -\sin{(2x)}$

---

Graph of Cosine Squared x VS. The Derivative of Cosine Squared x

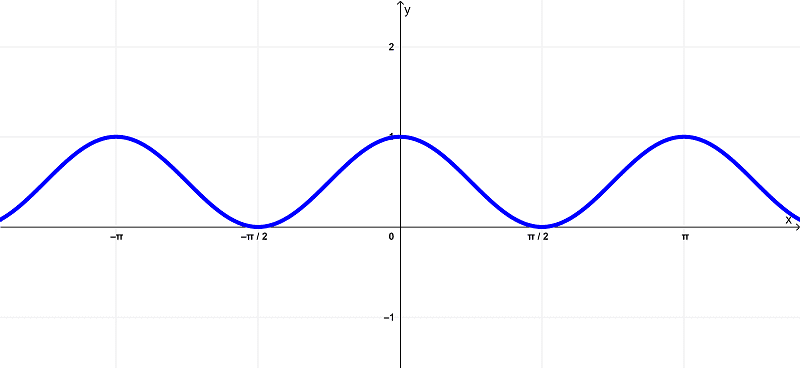
The graph of the function

$latex f(x) = \cos^{2}{(x)}$

is

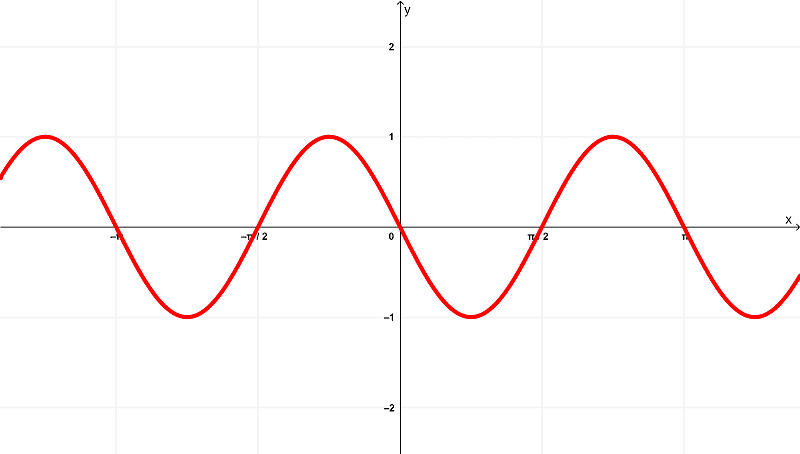
When deriving $latex f(x) = \cos^{2}{(x)}$, we get

$latex f'(x) = -\sin{(2x)}$

which has the following graph

Comparing their graphs, we have:

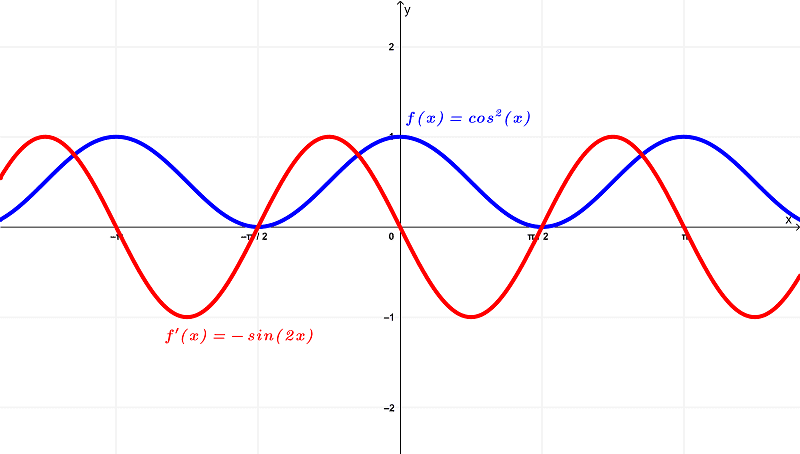
Using these graphs, we can see that the original function $latex f(x) = \cos^{2}{(x)}$ has a domain of

$latex (-\infty,\infty)$ or all real numbers

and exists within the range of

$latex [0,1]$

whereas the derivative $latex f'(x) = -\sin{(2x)}$ has a domain of

$latex (-\infty,\infty)$ or all real numbers

and exists within the range of

$latex [-1,1]$

---

Examples

In the following examples, we can learn how to derive composite cosine square functions.

Practice of derivatives of cosine square functions

---

See also

Interested in learning more about the derivatives of trigonometric functions squared? Take a look at these pages:

• Derivative of Sine Squared, sin^2(x) with Proof and Graphs
• Derivative of Tangent Squared, tan^2(x) with Proof and Graphs
• Derivative of Secant Squared, sec^2(x) with Proof and Graphs
• Derivative of Cosecant Squared, csc^2(x) with Proof and Graphs
• Derivative of Cotangent Squared, cot^2(x) with Proof and Graphs