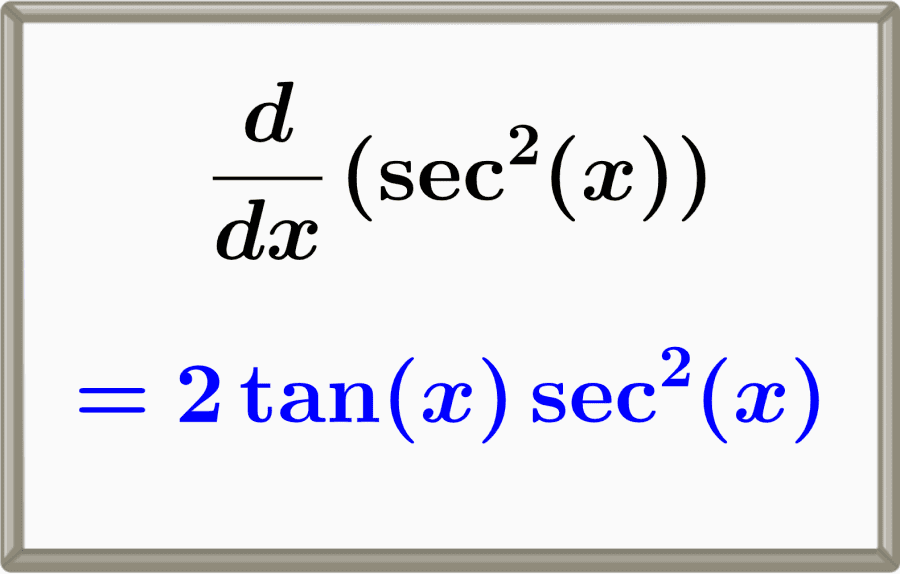Derivative of Secant Squared, sec^2(x) with Proof and Graphs

Proof of The Derivative of Secant Squared Function

As a prerequisite, please review the chain rule formula and its proof by looking here: Chain Rule of derivatives. Similarly, you can review the proof of the derivative of secant function by visiting this link: Derivative of Secant, sec(x).

Please be reminded that

$latex \sec^{2}{(x)} \neq \sec{(x^2)}$

We can identify the two functions that make up F(x). There is a power function and a trigonometric function in this scenario. To be more exact, it is a function raised to a power of two and a trigonometric function of secant, based on our given F(x).

For a better representation, we can rewrite it as

$latex F(x) = \sec^{2}{(x)}$

We can identify the two functions that make up F(x). There is a power function and a trigonometric function in this scenario. To be more exact, these are a function raised to a power of two and a trigonometric function of secant, based on our given F(x).

For a better representation, we can rewrite it as

$latex F(x) = \sec^{2}{(x)}$

$latex F(x) = (\sec{(x)})^2$

It becomes evident that the given power function is the outer function to be considered, while the secant function, being raised by the given power function, is the inner function. We can configure the outer function as follows:

$latex f(u) = u^2$

where

$latex u = \sec{(x)}$

The trigonometric secant function, as the inner function of f(u), will be denoted as g(x).

$latex f(u) = f(g(x))$

$latex u = g(x)$

$latex g(x) = \sec{(x)}$

Deriving the outer function f(u) using the power rule in terms of u, we have

$latex f(u) = u^2$

$latex f'(u) = 2u$

Deriving the inner function g(x) using the derivative formula of trigonometric function secant in terms of x, we have

$latex g(x) = \sec{(x)}$

$latex g'(x) = \sec{(x)}\tan{(x)}$

Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have

$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$

$latex \frac{dy}{dx} = (2u) \cdot (\sec{(x)}\tan{(x)})$

Substituting u into f'(u), we have

$latex \frac{dy}{dx} = (2(\sec{(x)})) \cdot (\sec{(x)}\tan{(x)})$

$latex \frac{dy}{dx} = 2\sec^{2}{(x)} \cdot \tan{(x)}$

which brings us to the derivative formula of secant squared x

$latex \frac{d}{dx} \sec^{2}{(x)} = 2\tan{(x)}\sec^{2}{(x)}$

---

Why are the derivative of secant squared and tangent squared the same?

You may wonder why

$latex \sec^{2}{(x)}$

and

$latex \tan^{2}{(x)}$

have similar derivatives.

Recall that the Pythagorean identity for secants and tangents is

$latex \sec^{2}{(x)} = 1 + \tan^{2}{(x)}$

Then, we can derive both sides of this equation to obtain:

$latex \frac{d}{dx} (\sec^{2}{(x)}) = \frac{d}{dx}(1) + \frac{d}{dx}(\tan^{2}{(x)})$

The derivative of a constant is equal to zero, so:

$latex \frac{d}{dx} (\sec^{2}{(x)}) = 0 + \frac{d}{dx}(\tan^{2}{(x)})$

$latex \frac{d}{dx} (\sec^{2}{(x)}) = \frac{d}{dx}(\tan^{2}{(x)})$

This is why both the secant squared and the tangent squared have the same derivative, because of the Pythagorean formula for secants and tangents.

---

Graph of Secant Squared x VS. The Derivative of Secant Squared x

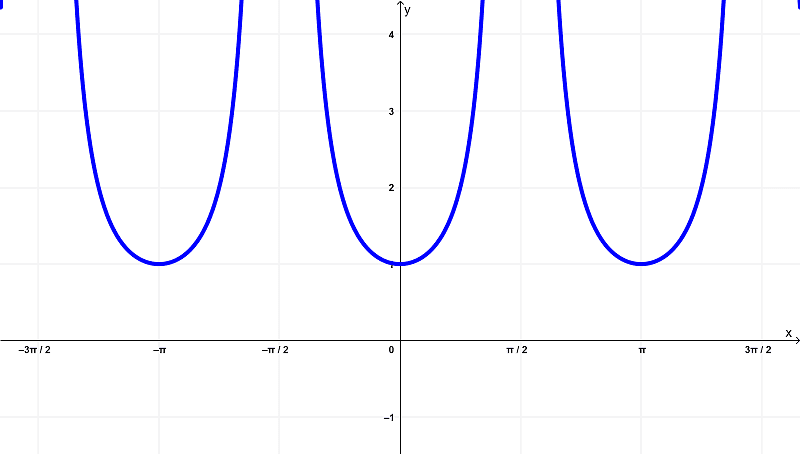
With the function

$latex f(x) = \sec^{2}{(x)}$

it is graphed as

If we derive the function $latex f(x) = \sec^{2}{(x)}$, we have

$latex f'(x) = 2\tan{(x)}\sec^{2}{(x)}$

and its graph is

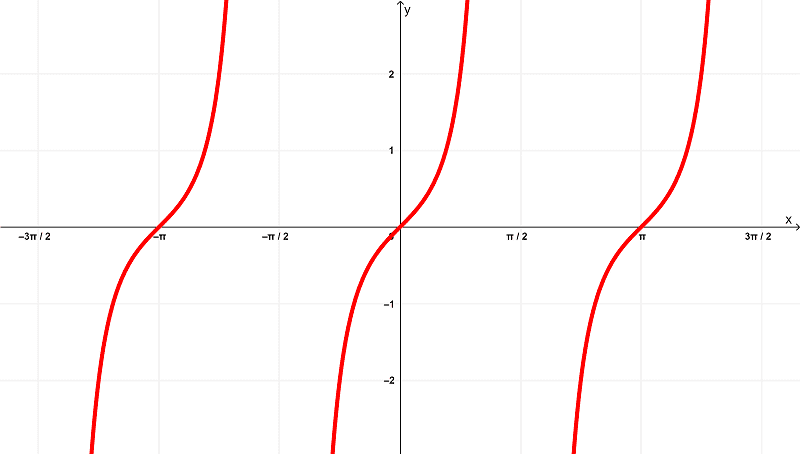
Illustrating both graphs in one, we have

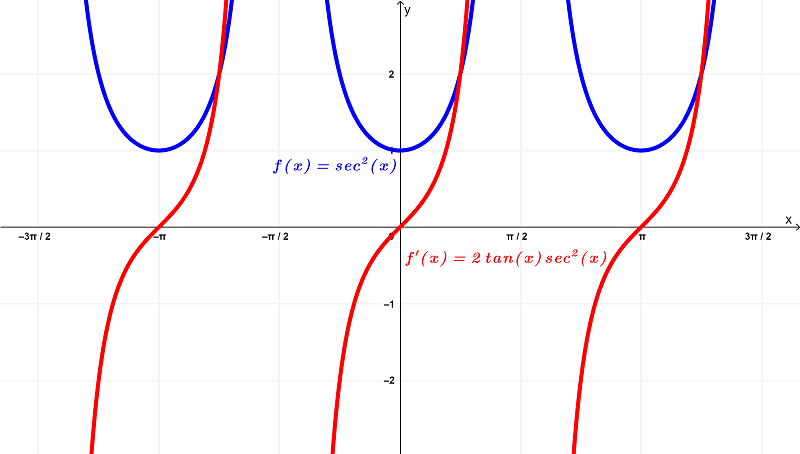
By examining these graphs, it can be seen that the original function $latex f(x) = \sec^{2}{(x)}$ has a domain of

$latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$

within the finite intervals of

$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$

and lies within the range of

$latex [1,\infty)$

whereas the derivative $latex f'(x) = 2\tan{(x)}\sec^{2}{(x)}$ has a domain of

$latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$

within the finite intervals of

$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$

and lies within the range of

$latex (-\infty,\infty)$

---

Examples

In the following examples, we can learn how to derive composite secant squared functions.

Practice of derivatives of secant squared functions

---

See also

Interested in learning more about the derivatives of trigonometric functions squared? Take a look at these pages:

• Derivative of Cosine Squared, cos^2(x) with Proof and Graphs
• Derivative of Sine Squared, sin^2(x) with Proof and Graphs
• Derivative of Tangent Squared, tan^2(x) with Proof and Graphs
• Derivative of Cosecant Squared, csc^2(x) with Proof and Graphs
• Derivative of Cotangent Squared, cot^2(x) with Proof and Graphs