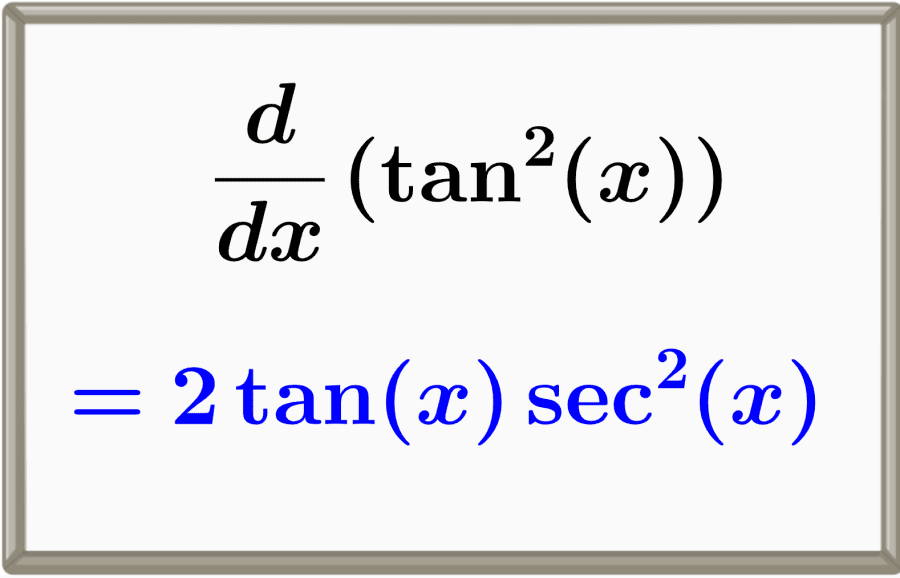Derivative of Tangent Squared, tan^2(x) with Proof and Graphs

Proof of The Derivative of Tangent Squared Function Using Chain Rule

You are encouraged to review the chain rule formula, as a prerequisite of this topic, by visiting this link: Chain Rule of derivatives. Likewise, you may visit this another link for the proof of the derivative of tangent function: Derivative of Tangent, tan(x).

Please take note that

$latex \tan^{2}{(x)} \neq \tan{(x^2)}$

We can use the chain rule to derive this function since it is a composite function. Therefore, we start with

$latex F(x) = \tan^{2}{(x)}$

We note that there are two functions that make up F(x), a power function and a trigonometric function. Specifically, they are a function raised to a power of two and a tangent function.

If we rewrite the function in the following way, we can visualize this in a better way:

$latex F(x) = \tan^{2}{(x)}$

$latex F(x)= (\tan{(x)})^2$

Now, we can clearly see that the tangent function is the inner function and the power function is the outer function. Then, we can write:

$latex f(u) = u^2$

where

$latex u = \tan{(x)}$

If we denote the tangent function as g(x), we have

$latex f(u) = f(g(x))$

$latex u = g(x)$

$latex g(x) = \tan{(x)}$

Deriving the outer function f(u) using the power rule in terms of u, we have

$latex f(u) = u^2$

$latex f'(u) = 2u$

Deriving the inner function g(x) using the derivative formula of trigonometric function tangent in terms of x, we have

$latex g(x) = \tan{(x)}$

$latex g'(x) = \sec^{2}{(x)}$

Algebraically multiplying the derivative of outer function $latex f'(u)$ by the derivative of inner function $latex g'(x)$, we have

$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$

$latex \frac{dy}{dx} = (2u) \cdot (\sec^{2}{(x)})$

Substituting u into f'(u), we have

$latex \frac{dy}{dx} = (2(\tan{(x)})) \cdot (\sec^{2}{(x)})$

$latex \frac{dy}{dx} = 2\tan{(x)} \cdot \sec^{2}{(x)}$

This gets us to the tangent squared x derivative formula.

$latex \frac{d}{dx} \tan^{2}{(x)} = 2\tan{(x)}\sec^{2}{(x)}$

---

Relationship between the derivative of the tangent squared and the secant squared

You may wonder why the derivative of both functions

$latex \tan^{2}{(x)}$

and

$latex \sec^{2}{(x)}$

are the same.

According to the Pythagorean formula for tangents and secants,

$latex \sec^{2}{(x)} = 1 + \tan^{2}{(x)}$

If we try to derive both sides of the equation, we have

$latex \frac{d}{dx} (\sec^{2}{(x)}) = \frac{d}{dx}(1) + \frac{d}{dx}(\tan^{2}{(x)})$

Evaluating the derivative of the first term in the right-hand-side of the equation, which is the derivative of a constant 1, we have

$latex \frac{d}{dx} (\sec^{2}{(x)}) = 0 + \frac{d}{dx}(\tan^{2}{(x)})$

$latex \frac{d}{dx} (\sec^{2}{(x)}) = \frac{d}{dx}(\tan^{2}{(x)})$

This is why both the tangent squared and the secant squared have the same derivative.

---

Graph of Tangent Squared x VS. The Derivative of Tangent Squared x

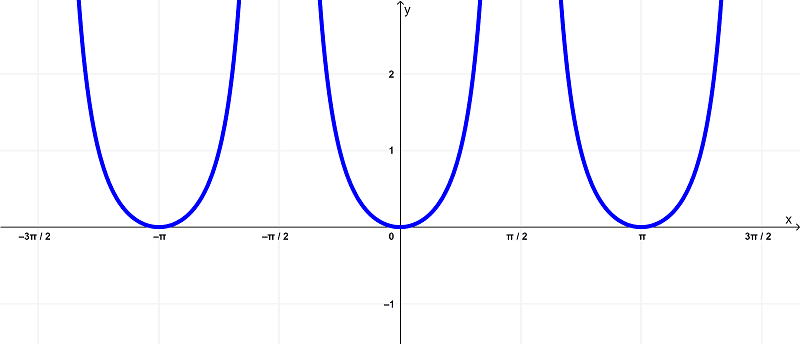
The graph of the function

$latex f(x) = \tan^{2}{(x)}$

is

Deriving $latex f (x) = \tan^{2}{(x)}$, we get

$latex f'(x) = 2\tan{(x)}\sec^{2}{(x)}$

which has the following graph

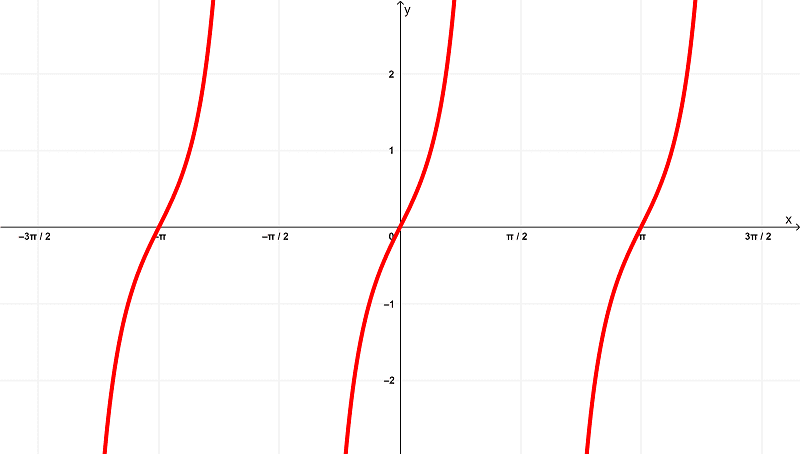
Comparing their graphs, we have

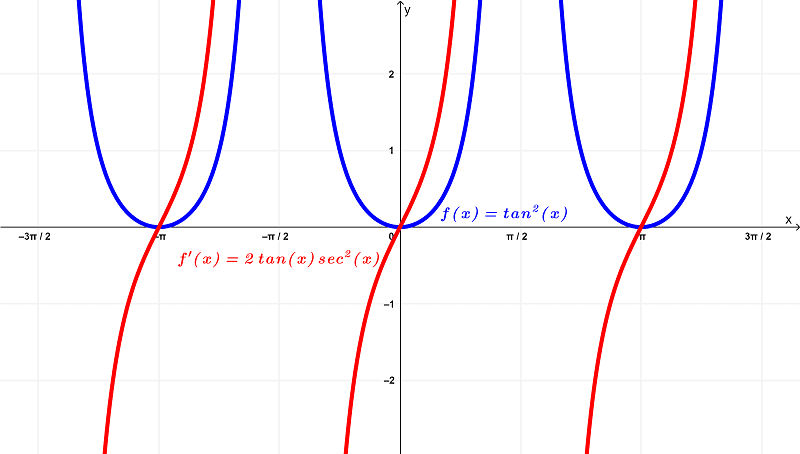
From the graphs, you can see that the original function $latex f(x) = \tan^{2}{(x)}$ has a domain of

$latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$

within the finite intervals of

$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$

and exists within the range of

$latex [0,\infty)$

whereas the derivative $latex f'(x) = 2\tan{(x)}\sec^{2}{(x)}$ has a domain of

$latex \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$

within the finite intervals of

$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$

and exists within the range of

$latex (-\infty,\infty)$

---

Examples

The following examples show how to find the derivative of a composite square tangent function.

Practice of derivatives of tangent squared

---

See also

Interested in learning more about the derivatives of trigonometric functions squared? Take a look at these pages:

• Derivative of Cosine Squared, cos^2(x) with Proof and Graphs
• Derivative of Sine Squared, sin^2(x) with Proof and Graphs
• Derivative of Secant Squared, sec^2(x) with Proof and Graphs
• Derivative of Cosecant Squared, csc^2(x) with Proof and Graphs
• Derivative of Cotangent Squared, cot^2(x) with Proof and Graphs