The derivative of the cosecant function is equal to minus cosecant times cotangent, -csc(x) cot(x). We can prove this derivative using limits and trigonometric identities.
In this article, we will learn how to derive the cosecant trigonometric function, both in its simple form and in its composite form. We will see a demonstration of its derivative, a graphical comparison of cosecant and its derivative, and some examples.
Proof of the Derivative of the Cosecant Function
The trigonometric function cosecant of an angle is defined as the ratio of hypothenuse to the opposite side of an angle in a right triangle. Illustrating it through a figure, we have
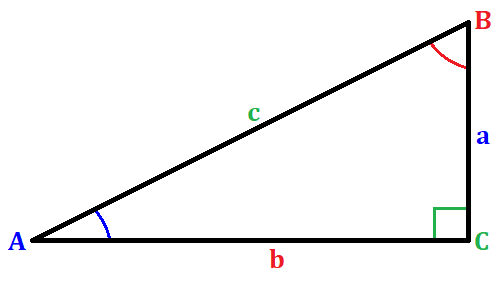
where C is 90°. For the sample right triangle, getting the cosecant of angle A can be evaluated as
$latex \csc{(A)} = \frac{c}{a}$
where A is the angle, c is the hypothenuse, and a is its opposite side.
Before learning the proof of the derivative of the cosecant function, you are hereby recommended to learn the Pythagorean theorem, Soh-Cah-Toa & Cho-Sha-Cao, and the first principle of limits as prerequisites.
To review, any function can be derived by equating it to the limit of
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Suppose we are asked to get the derivative of
$latex f(x) = \csc{(x)}$
we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \csc{(x+h)} – \csc{(x)} }{h}}$$
Analyzing our equation, we can observe that both the first and second terms in the numerator of the limit is a cosecant of a sum of two angles x and h and a cosecant of angle x. With this observation, we can try to apply the defining relation identities for cosecant and sine. Applying this, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{1}{\sin{(x+h)}} – \frac{1}{\sin{(x)}} }{h}}$$
Algebraically re-arranging by applying some rules of fractions, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{ \sin{(x)} – \sin{(x+h)} }{\sin{(x+h)}\sin{(x)}} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ \sin{(x)} – \sin{(x+h)} }{h\sin{(x+h)}\sin{(x)}} }$$
Looking at the re-arranged numerator, we can try to apply the product-sum identities of sine.
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ 2\cos{\left(\frac{x+(x+h)}{2}\right)} \sin{\left(\frac{x-(x+h)}{2}\right)} }{h\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ 2\cos{\left(\frac{x+x+h}{2}\right)} \sin{\left(\frac{x-x-h}{2}\right)} }{h\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ 2\cos{\left(\frac{2x+h}{2}\right)} \sin{\left(\frac{-h}{2}\right)} }{h\sin{(x+h)}\sin{(x)}} \right)}$$
Based on the trigonometric identities of a sine of a negative angle, it is equal to negative sine of the positive form of the same angle. Applying this to the second multiplicand of the numerator, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ 2\cos{\left(\frac{2x+h}{2}\right)} \cdot \left( -\sin{\left(\frac{h}{2}\right)} \right) }{h\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -2\cos{\left(\frac{2x+h}{2}\right)} \sin{\left(\frac{h}{2}\right)} }{h\sin{(x+h)}\sin{(x)}} \right)}$$
Re-arranging algebraically and by applying the limit of product of two functions, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -\cos{\left(\frac{2x+h}{2}\right)} \cdot 2\sin{\left(\frac{h}{2}\right)} }{\sin{(x+h)}\sin{(x)} \cdot h} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+h}{2}\right)} }{ \sin{(x+h)}\sin{(x)} } \cdot \frac{ 2\sin{\left(\frac{h}{2}\right)} }{h} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+h}{2}\right)} }{ \sin{(x+h)}\sin{(x)} } \right)} \cdot \lim \limits_{h \to 0} {\left( \frac{ 2\sin{\left(\frac{h}{2}\right)} }{h} \right)}$$
Applying some rules of fraction to the second multiplicand, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+h}{2}\right)} }{ \sin{(x+h)}\sin{(x)} } \right)} \cdot \lim \limits_{h \to 0} {\left( \frac{ \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } \right)}$$
In accordance with the limits of trigonometric functions, the limit of trigonometric function $latex \sin{(\theta)}$ to $latex \theta$ as $latex \theta$ approaches zero is equal to one. The same can be applied to $latex \sin{\left(\frac{h}{2}\right)}$ over $latex \frac{h}{2}$. Applying, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+h}{2}\right)} }{ \sin{(x+h)}\sin{(x)} } \right)} \cdot \lim \limits_{h \to 0} {1}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+h}{2}\right)} }{ \sin{(x+h)}\sin{(x)} } \right)}$$
Finally, we have successfully made it possible to evaluate the limit of whatever is left in the equation. Evaluating by substituting the approaching value of $latex h$, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x+(0)}{2}\right)} }{ \sin{(x+(0))}\sin{(x)} } \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{-\cos{\left(\frac{2x}{2}\right)} }{ \sin{(x)}\sin{(x)} } \right)}$$
$$\frac{d}{dx} f(x) = \frac{-\cos{(x)} }{ \sin{(x)}\sin{(x)} }$$
$$\frac{d}{dx} f(x) = -\frac{\cos{(x)} }{ \sin{(x)}\sin{(x)} }$$
Applying some trigonometric identities to simplify the derivative formula by the use of defining relation identities, we have
$$\frac{d}{dx} f(x) = -\frac{ \cos{(x)} }{ \sin{(x)} } \cdot \frac{1}{\sin{(x)}} $$
$$\frac{d}{dx} f(x) = -\cot{(x)} \cdot \csc{(x)} $$
$$\frac{d}{dx} f(x) = -\csc{(x)} \cot{(x)}$$
Therefore, the derivative of the trigonometric function ‘cosecant‘ is:
$$\frac{d}{dx} (\csc{(x)}) = -\csc{(x)} \cot{(x)}$$
Graph of Cosecant x VS. The Derivative of Cosecant x
Given the function
$latex f(x) = \csc{(x)}$
the graph is illustrated as
And as we know by now, by deriving $latex f(x) = \csc{(x)}$, we get
$latex f'(x) = -\csc{(x)}\cot{(x)}$
which is illustrated graphically as
Illustrating both graphs in one, we have
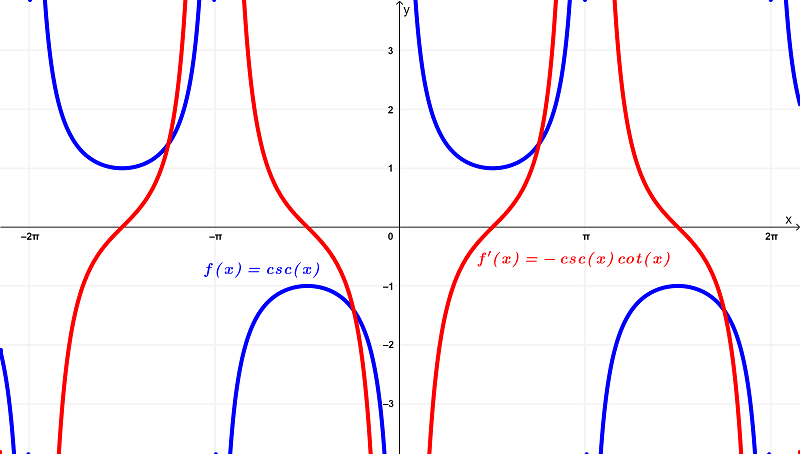
From the graphical comparison, it can be seen that the original function $latex f(x) = \csc{(x)}$ has a domain of
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
within the finite intervals of
$latex (-2\pi,2\pi)$
and exists within the range of
$latex (-\infty,-1] \cup [1,\infty)$
whereas the derivative $latex f'(x) = -\csc{(x)}\cot{(x)}$ has a domain of
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
within the finite intervals of
$latex (-2\pi,2\pi)$
and exists within the range of
$latex (-\infty,\infty)$ or all real numbers
Examples
The following are some examples of how to use the chain rule to derive composite cosecant functions.
EXAMPLE 1
What is the derivative of $latex f(x) = \csc(8x)$?
Solution
We have a composite cosecant function, where $latex u=8x$ is the inner function. This means that we can write $latex f(u)=\csc(u)$.
Then, let’s use the chain rule as follows:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\csc(u)\cot(u) \times 8$$
Now, we just have to substitute $latex u=8x$ back into the function and we have:
$$\frac{dy}{dx}=-8\csc(8x)\cot(8x)$$
EXAMPLE 2
Calculate the derivative of $latex F(x) = \csc(6x^2-3)$.
Solution
Let’s use the chain rule to derive this function. Then, we express the cosecant function as $latex f (u) = \csc(u)$, where $latex u = 6x^2-3$.
Then, we calculate the derivative of the function $latex f (u) = \csc(u)$:
$$\frac{d}{du} ( \csc{(u)} ) = -\csc(u)\cot(u)$$
Now, we calculate the derivative of the inner function $latex u = 6x^2-3$, which we call $latex g(x)$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(6x^2-3)$$
$$\frac{d}{dx}(g(x)) = 12x$$
To apply the chain rule, we multiply the derivative of the outer function by the derivative of the inner function:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\csc(u)\cot(u) \cdot 12x$$
Finally, we substitute $latex u=6x^2-3$ back:
$$\frac{dy}{dx} = -\csc(6x^2-3)\cot(6x^2-3) \cdot 12x$$
$$\frac{dy}{dx} = -12x\csc(6x^2-3)\cot(6x^2-3)$$
EXAMPLE 3
Find the derivative of $latex f(x) = \csc(\sqrt{x})$
Solution
To derive this function, we use the chain rule and consider $latex u=\sqrt{x}$ as the inner function.
Now, we write $latex u=\sqrt{x}$ as $latex u=x^{\frac{1}{2}}$ to find the derivative of $latex \frac{du}{dx}$:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Then, since we have $latex f(u)=\csc(u)$, we use the chain rule:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\csc(u)\cot(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Substituting $latex u=\sqrt{x}$ back and simplifying, we have:
$$\frac{dy}{dx}=-\csc(\sqrt{x})\cot(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}}\csc(\sqrt{x})\cot(\sqrt{x})$$
Practice of derivatives of composite cosecant functions
See also
Interested in learning more about the derivatives of trigonometric functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
