Trigonometric equations are equations involving trigonometric functions such as sine, cosine, and tangent. These equations can be used to solve a wide variety of problems, from finding the height of a building to calculating the velocity of an object moving in a circular path.
In this article, we will explore the basics of trigonometric equations and discuss how to solve them using various techniques.
How to solve trigonometric equations?
Trigonometric equations are solved following the same strategies used in other types of equations, with the goal of isolating the variable and determining the values it takes.
The objective is to use trigonometric identities and apply operations on both sides of the equation until the simplest possible version is obtained.
An example of a simple trigonometric equation is $latex \cos(\theta)=\frac{1}{2}$. In this case, the angle that would satisfy this equation is 60°.
However, since the cosine function is periodic, we know that there are other solutions to this equation.
Sketching the graph of $latex y=\cos(\theta)$ and $latex y=\frac{1}{2}$, we have:
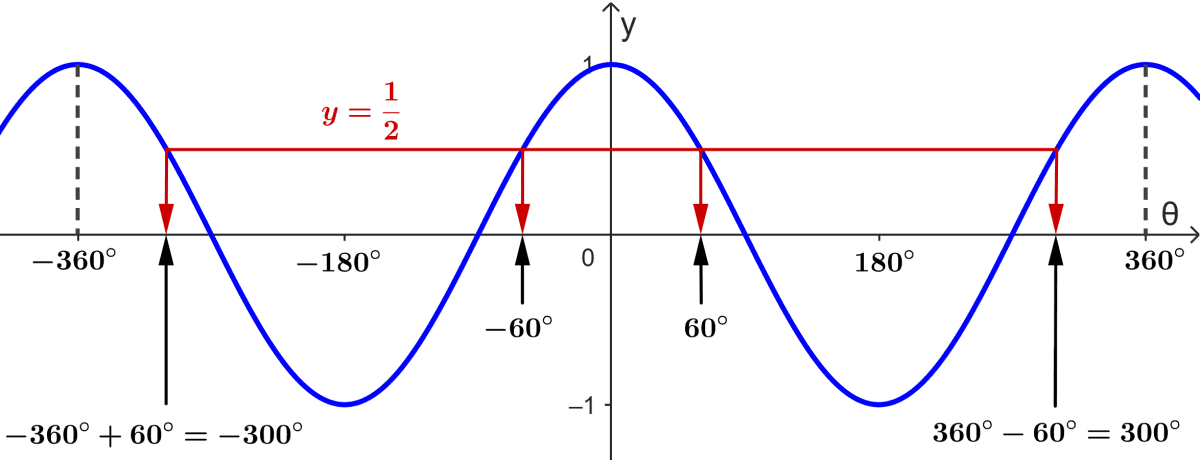
This shows us that in the range $latex -360^{\circ}\leq \theta \leq 360^{\circ}$ there are four solutions to the equation $latex \cos(\theta)=\frac{1}{ 2}$: $latex ~\theta=\pm 60^{\circ},~\pm 300^{\circ}$.
If no range for $latex \theta$ is specified, there are an infinite number of solutions. For this reason, the trigonometric equations are accompanied by a range for $latex \theta$.
Trigonometric equations – Examples with answers
EXAMPLE 1
Solve the trigonometric equation:
$$\tan^2x-3=0$$
For $latex 0\leq x\leq 360º$
Solution
We can write as follows:
$$\tan^2x-3=0\Rightarrow\tan^2x=3$$
$$\tan x=\pm\sqrt{3}$$
The unknown is isolated by using the corresponding inverse trigonometric function:
$$x =\arctan (\pm\sqrt{3})$$
That is, we must find all the angles whose tangent is $latex \pm\sqrt{3}$ and which at the same time belong to the interval $latex 0\leq x\leq 360º$. The equation has four of these solutions:
- $latex x_1 = 60º$
- $latex x_2 = 120º$
- $latex x_3 = 240º$
- $latex x_4 = 300º$
The reader can easily verify that:
$latex \tan 60º=\sqrt {3}=\tan 240º$
Whereas:
$latex \tan 120º=-\sqrt {3}=\tan 300º$
EXAMPLE 2
Find the solutions to the equation:
$$2\cos x -6=-4$$
In the interval $latex 0\leq x\leq 180º$
Solution
$$2\cos x -6=-4\Rightarrow 2\cos x=2$$
$$\cos x=1$$
Therefore:
$$x=\arccos 1$$
The solution of this equation in the requested interval is:
$latex x = 0º$
EXAMPLE 3
Find the solutions of the trigonometric equation:
$$2\cos^2x-\sin x-1=0$$
In the interval: $latex 0\leq x\leq 360º$
Solution
In this equation, we see that the variable $latex x$ is in the argument of cosine and sine, so the first step is to write the equation in terms of a single trigonometric function, for which a trigonometric identity relating them is required.
This identity is: $latex \cos^2 x + \sin^2 x = 1$.
We can now rewrite it to express cosine in terms of sine:
$latex \cos^2 x = 1- \sin^2 x$
And this is substituted into the original equation:
$$2\cos^2x-\sin x-1=0\Rightarrow 2(1- \sin^2 x)-\sin x-1=0$$
Leading to:
$$2- 2\sin^2 x-\sin x-1=0$$
$$- 2\sin^2 x-\sin x+1=0$$
Multiplying both sides by $latex -1$, we have:
$$2\sin^2 x+\sin x-1=0$$
Now the following variable substitution is made:
$latex y=\sin x $
And the equation is transformed into:
$$2y^2 +y-1=0$$
This is a second-degree equation of $latex y$ that is easily solved by factoring:
$$2y^2 +y-1=(2y-1)(y+1)=0$$
The roots of this equation are:
$latex y_1 =\dfrac{1}{2}$
$latex y_2 =-1$
The next step is to substitute back, which leads to two simple equations:
Equation 1
$$\sin x =\dfrac{1}{2}\Rightarrow x=\arcsin \left(\dfrac{1}{2}\right)$$
In the interval $latex 0\leq x\leq 360º$ there are two angles whose sine equal $latex \dfrac{1}{2}$, and they are:
- $latex x_1 =30º$
- $latex x_2 = 150º$
Equation 2
$$\sin x =-1\Rightarrow x=\arcsin (-1)$$
In the interval $latex 0\leq x\leq 360º$ there is a single angle whose sine equals $latex -1$, and it is:
- $latex x_3=270º$
EXAMPLE 4
Find the solutions to the equation:
$$\tan x+\sec^2 x – 3 = 0$$
Solution
As in the previous example, we need to have only one trigonometric function in the equation, and since tangent and secant appear here, we use the identity:
$latex \sec^2 x = 1+\tan ^2x$
Substituting in the original equation, it becomes:
$$\tan x+\sec^2 x – 3 = 0\Rightarrow \tan x+(1+\tan ^2x) – 3 = 0 $$
Therefore, the equation is:
$$ \tan ^2x+\tan x- 2 = 0 $$
This equation is also transformed into a quadratic equation by substituting $latex y=\tan x $ in:
$$y^2 +y-2=0$$
Easily solved by factoring:
$$y^2 +y-2=(y+2)(y-1)=0$$
And the roots are:
$latex y_1 =-2$
$latex y_2 =1$
Substituting back, this leads to two simple equations:
Equation 1
$latex \tan x =-2$
And the solution is:
$latex x = \arctan (-2)$
- $latex x_1=-63,4º; 116.6º; -243.40º;…$
Note that the statement did not specify an interval for the solution. When the solutions of a trigonometric equation lie in the interval $latex 0\leq x\leq 360º$, they are called main solutions.
But, due to the periodicity of trigonometric functions, there are an infinite number of solutions to $latex x = \arctan (-2)$ , which can be given in a general and compact form:
- $latex x_1 = k\cdot180º-63.4º$
Where $latex k$ is an integer, that is, $latex k = \pm 1;\pm 2; \pm 3; \pm 4…$
Equation 2
$latex \tan x =1$
Where it follows that:
$latex x = \arctan (1)$
- $latex x_2= 45º; 225º; -135º;…$
- $latex x_2 = k\cdot 180º+45º$
If preferred, the solution can be given in radians, as follows:
- $latex x_2 =k\pi+\dfrac{\pi}{4}$
Where $latex \dfrac{\pi}{4}=45º$, or:
- $latex x_2=\dfrac{(4k+1)\pi}{4}$
Where $latex k =0; \pm 1;\pm 2; \pm 3; \pm 4…$
EXAMPLE 5
Determine the solution to the trigonometric equation:
$$\sin 2x +\cos x = 0$$
Within the interval given by: $latex 0\leq x\leq 360º$
Solution
Since the argument of sine and cosine are not the same, we use a trigonometric identity that relates $latex \sin 2x$ to $latex \sin x$ or $latex \cos x$, so that the argument is $ latex x$.
This identity is that of the double angle:
$latex \sin 2x =2\sin x\cos x$
Which, when substituted into the original equation, gives as this result:
$$\sin 2x +\cos x = 0\Rightarrow 2\sin x\cos x+\cos x=0$$
The equation obtained is factored to find the solutions, leaving:
$$\cos x(2\sin x+1)=0$$
From there, two simpler equations are obtained:
Equation 1
$latex \cos x=0$
$latex x =\arccos 0$
Whose solutions, in the interval indicated in the statement, are:
- $latex x_1 =90º=\dfrac{\pi}{2}$
- $latex x_2 =270º=\dfrac{3\pi}{2}$
Equation 2
$latex 2\sin x+1=0\Rightarrow 2\sin x=-1$
$latex \sin x=-\dfrac{1}{2}$
$latex x=\arcsin\left(-\dfrac{1}{2}\right)$
Which gives us two solutions in the indicated interval:
- $latex x_3 =210º=\dfrac{7\pi}{6}$
- $latex x_4 =330º=\dfrac{11\pi}{6}$
EXAMPLE 6
Solve the following trigonometric equation:
$$3\sin x-\sqrt{3}\cos x=0$$
Solution
This trigonometric equation is of the form:
$latex a\sin x + b\cos x = 0$
Which is easily solved by dividing both sides of the equality by $latex \cos x$, to leave everything in terms of $latex \tan x$:
$$3\sin x-\sqrt{3}\cos x=\frac{3\sin x-\sqrt{3}\cos x}{\cos x}=0$$
This equation becomes:
$$3\tan x-\sqrt{3}=0$$
Therefore:
$$3\tan x=\sqrt{3}\Rightarrow\tan x=\frac{\sqrt{3}}{3}$$
$$x = \arctan \dfrac{\sqrt{3}}{3}$$
Since the statement did not specify an interval, it means that there are infinite solutions:
- $latex x_1 = 30º, 210º, 390º, 570º…$
And its general form is:
- $latex x = k\pi+\dfrac{\pi}{6}$
Or:
- $latex x = k\cdot 180º+30º$
Where $latex k = 0, \pm 1, \pm 2, \pm 3…$
EXAMPLE 7
Solve the trigonometric equation:
$$4\sin x+3\cos x = 3$$
Solution
To solve this equation, which contains an independent term other than $latex 0$, the following change of variable is used:
$$t=\tan \left(\dfrac{x}{2}\right)$$
Thus, sine and cosine are expressed as follows:
$$\cos x=\dfrac{1-t^2}{1+t^2}$$
$$\sin x=\dfrac{2t}{1+t^2}$$
This change of variable is known as the universal substitution or Weierstrass substitution. Then, the original equation looks like this:
$$4\sin x+3\cos x = 3\Rightarrow 4\left(\frac{2t}{1+t^2}\right) +3\left(\frac{1-t^2}{1+t^2}\right)=3$$
$$\frac{8t+3-3t^2}{1+t^2}=3\Rightarrow 8t+3-3t^2=3+3t^2$$
Regrouping the terms, we obtain a quadratic equation in $latex t$:
$$-6t^2+8t=0$$
$$3t^2-4t=0$$
Which is solved by factoring:
$$3t^2-4t=0\Rightarrow t(3t-4)=0$$
The solutions are:
$latex t_1 =0$
$latex t_2=\dfrac{4}{3}$
This leads to two simple equations, by substituting back:
Equation 1
$$\tan \left(\dfrac{x}{2}\right)=0$$
Therefore:
$latex\dfrac{x}{2}=\arctan 0$
$latex \dfrac{x}{2}=0, \pm\pi, \pm 2\pi, \pm 3\pi,…$
$latex x=0, \pm 2\pi, \pm 4\pi, \pm 6\pi,…$
$latex x=2k\pi=2k\cdot 360º$
Where $latex k$ is an integer.
Equation 2
$$\tan \left(\dfrac{x}{2}\right)=\dfrac{4}{3}$$
We deduce that:
$latex \dfrac{x}{2}=\arctan \left(\dfrac{4}{3}\right)=53.1º$
Therefore, the main solution, which is in the interval $latex 0\leq x\leq 360º$, is:
$latex x=106.2º$
Furthermore, the angles $latex -253.8º, 466.2º,…$ are also solutions of the proposed equation, since the tangent function is periodic, therefore, in general form, the solution is given by:
$latex x = k\cdot 360º+ 106.2º$
Where $latex k = 0,\pm 1, \pm 2, \pm 3…$, that is, $latex k$ is an integer.
EXAMPLE 8
Find the main solutions of the equation:
$$3\sin^2x-\cos^2x =0$$
Solution
If the Pythagorean identity is used:
$latex \sin^2x+\cos^2x$
$latex \cos^2x=1-\sin^2x$
Then:
$$3\sin^2x-\cos^2x =0\Rightarrow 3\sin^2x-(1-\sin^2x )=0 $$
Therefore:
$$4\sin^2x-1 =0$$
$$\sin^2x=\dfrac{1}{4}\Rightarrow \sin x = \pm \sqrt \frac{1}{4}=\pm\dfrac{1}{2}$$
Therefore, the principal solutions of the equation are:
- $latex x_1=\arcsin \left(\dfrac{1}{2}\right)=30º$
- $latex x_2=\arcsin \left(-\dfrac{1}{2}\right)=210º$
EXAMPLE 9
Find the general solution of:
$$\cos x=\dfrac{2\tan x}{1+\tan^2x}$$
Solution
To solve this equation, the following identities are used:
$latex \sec^2=1+\tan^2x$
$latex \sec x = \dfrac{1}{\cos x}$
$latex \tan x=\dfrac{\sin x}{\cos x}$
Then, we have:
$$\cos x=\dfrac{2\tan x}{1+\tan^2x}=\dfrac{\dfrac{2\sin x}{\cos x}}{\sec^2x}=$$
$$=\dfrac{\dfrac{2\sin x}{\cos x}}{\dfrac{1}{\cos^2x}}=2\sin x \cos x$$
Therefore:
$$\cos x = 2\sin x \cos x$$
Dividing both sides by $latex \cos x$, as long as $latex \cos x\neq 0$:
$$\cos x = 2\sin x \cos x\Rightarrow \dfrac{\cos x}{\cos x}=\dfrac{2\sin x \cos x}{\cos x}$$
Leading to:
$$2\sin x=1$$
Then:
$$x=\arcsin\left(\dfrac{1}{2}\right)$$
$latex x = 30º, 150º,…-330º,… $
In general form, the solution is:
$latex x = 30º+k\cdot180º$
Or also:
$latex x=\dfrac{\pi}{6}+k\pi$
Where $latex k$ is an integer.
EXAMPLE 10
Solve the following system of equations:
$$ \left\{\begin{array}{rcl} \sin x+\cos y&=&\sqrt{2}\\ \cosec x+\sec y&=&2\sqrt{2} \end{array}\right.$$
Solution
Using the following change of variable: $latex p = \sin x$, $latex ~q=\cos y$, the system of equations looks like this:
$$ \left\{\begin{array}{rcl} p+q&=&\sqrt{2}\\ \frac{1}{p}+\frac{1}{q}&=&2\sqrt{2} \end{array}\right.$$
From the first equation, we get:
$latex p =\sqrt{2}-q$
It is then substituted into the second equation:
$$\left(\dfrac{1}{\sqrt{2}-q}\right)+\left(\dfrac{1}{q}\right)=2\sqrt{2}$$
$$\dfrac{q+\sqrt{2}-q}{q(\sqrt{2}-q)}=2\sqrt{2}$$
$$\dfrac{\sqrt{2}}{q(\sqrt{2}-q)}=2\sqrt{2}$$
Therefore:
$$q(\sqrt{2}-q)=0.5$$
Applying the distributive property, we obtain a second-degree equation:
$latex q^2-\sqrt{2}q+0.5=0$
Whose solution is:
$latex q=\dfrac{\sqrt{2}}{2}=0.70710…$
Substituting:
$latex p =\sqrt{2}-q$
We get:
$$p =\sqrt{2}-\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}=0.70710…$$
Substituting back, we get:
$$p = \sin x\Rightarrow\sin x=\dfrac{\sqrt{2}}{2}\Rightarrow x=\arcsin\left(\dfrac{\sqrt{2}}{2}\right)$$
And the general solution is:
$$x = 2k\pi+\dfrac{\pi}{4}$$
Where $latex k$ is an integer.
On the other hand:
$latex q = \cos y$
$$q = \cos y\Rightarrow\cos y=\dfrac{\sqrt{2}}{2}\Rightarrow y=\arccos\left(\dfrac{\sqrt{2}}{2}\right)$$
$$ y = 2k\pi+\dfrac{\pi}{4}$$
Where $latex k$ is an integer.
Trigonometric equations – Practice problems


Solve the following equation for $latex \theta$, where $latex -180^{\circ}\leq \theta\leq 180^{\circ}$. $$\cosec(\theta)+\sin(\theta)+2=0$$
Write the answer in degrees.
See also
Interested in learning more about trigonometric equations? You can take a look at these pages:




