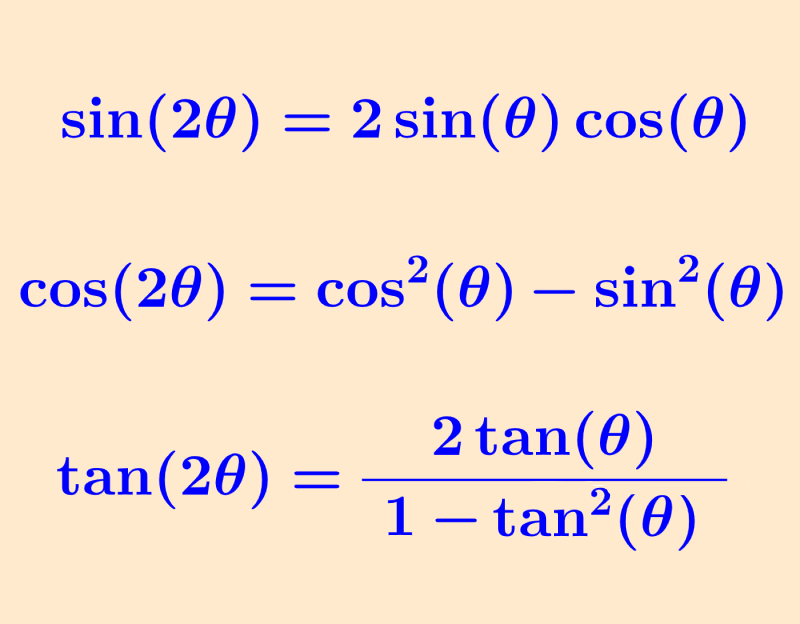Double angle identities are trigonometric identities used to rewrite trigonometric functions, such as sine, cosine, and tangent, that have a double angle, such as 2θ. These identities are derived using the angle sum identities. We have a total of three double angle identities, one for cosine, one for sine, and one for tangent. However, these identities can have different variations.
Here, we will learn how to derive double-angle identities. Then, we will apply these identities to solve some practice problems.
What are the double angle identities?
Double angle identities are trigonometric identities that are used when we have a trigonometric function that has an input that is equal to twice a given angle. For example, we can use these identities to solve $latex \sin (2\theta)$.
In this way, if we have the value of θ and we have to find $latex \sin (2 \theta)$, we can use this identity to simplify the problem.
The following is the formula that expresses the double angle identity for the sine:
| $latex \sin(2x)=2\sin(x)\cos(x)$ |
The following is the formula that expresses the double angle identity for the cosine. This identity can have two additional variations that are obtained when using the Pythagorean identity:
| $latex \cos(2x)={{\cos}^2}(x)-{{\sin}^2}(x)$ $latex =2{{\cos}^2}(x)-1$ $latex =1-2{{\sin}^2}(x)$ |
The following is the formula that expresses the double angle identity for the tangent:
| $latex \tan(2x)=\frac{2\tan(x)}{1-{{\tan}^2}(x)}$ |
Proof of the double angle identities
The double angle identities are derived using the angle sum identities.
In the case of the sum of angles in a sine, we have:
$$\sin(\alpha + \beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)$$
If α and β were the same angle, we would have:
$$\sin(\alpha + \alpha)=\sin(\alpha)\cos(\alpha)+\cos(\alpha)\sin(\alpha)$$
$latex \sin(2\alpha)=2\sin(\alpha)\cos(\alpha)$
This is the identity of the double angle for the sine. Using the same process, we find the identity of the double angle for the cosine. Therefore, we start with the cosine angle sum identity:
$$\cos(\alpha + \beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)$$
Now, we use the same angle and we have:
$$\cos(\alpha + \alpha)=\cos(\alpha)\cos(\alpha)-\sin(\alpha)\sin(\alpha)$$
$latex \cos(2\alpha)={{\cos}^2}(\alpha)-\sin^2(\alpha)$
We can derive two additional variations of this identity using the Pythagorean identity, $latex {{\sin}^2}(\alpha)+\cos^2(\alpha)=1$. This identity can be written as $latex {{\sin}^2}(\alpha)=1-\cos^2(\alpha)$ y $latex {{\cos}^2}(\alpha)=1-{{\sin}^2}(\alpha)$.
If we use $latex {{\sin}^2}(\alpha)=1-{{\cos}^2}(\alpha)$, we have:
$latex \cos(2\alpha)={{\cos}^2}(\alpha)-{{\sin}^2}(\alpha)$
$latex ={{\cos}^2}(\alpha)-(1-{{\cos}^2}(\alpha))$
$latex ={{\cos}^2}(\alpha)-1+{{\cos}^2}(\alpha))$
$latex =2{{\cos}^2}(\alpha)-1$
If we use $latex {{\cos}^2}(\alpha)=1-{{\sin}^2}(\alpha)$, we have:
$latex \cos(2\alpha)={{\cos}^2}(\alpha)-{{\sin}^2}(\alpha)$
$latex =1-{{\sin}^2}(\alpha)-{{\sin}^2}(\alpha)$
$latex =1-2{{\sin}^2}(\alpha)$
Now, we use the tangent angle sum identity formula to calculate its double angle formula. Therefore, we start with:
$$\tan(\alpha+\beta)=\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}$$
If we have the same angle, the formula becomes:
$$\tan(\alpha+\alpha)=\frac{\tan(\alpha)+\tan(\alpha)}{1-\tan(\alpha)\tan(\alpha)}$$
$$\tan(2\alpha)=\frac{2\tan(\alpha)}{1-{{\tan}^2}(\alpha)}$$
Double angle identities – Examples with answers
The double angle identities of the sine, cosine, and tangent are used to solve the following examples. Try to solve the examples yourself before looking at the answer.
EXAMPLE 1
If we have $latex \sin(A) = \frac{5}{13}$ and $latex \cos(A)= – \frac{12}{13}$, what is the value of $latex \sin(2A)$?
Solution
We know the sine of A and cosine of A, so we can apply the double angle formula for the sine directly. Therefore, we have:
$latex \sin(2A)=2\sin(A)\cos(A)$
$latex \sin(2A)=2(\frac{5}{13})(-\frac{12}{13})$
$latex \sin(2A)=-\frac{120}{169})$
EXAMPLE 2
If we have $latex \sin(A) = \frac{5}{13}$ and $latex \cos(A) = – \frac{12}{13}$, what is the value of $latex \cos(2A)$?
Solution
In this case, we want to find the cosine value of the double angle of A. Therefore, we use the formula seen above with the given sine and cosine values:
$latex \cos(2A)={{\cos}^2}(A)-{{\sin}^2}(A)$
$latex \cos(2A)={{(-\frac{12}{13})}^2}-{{(\frac{5}{13})}^2}$
$latex \cos(2A)=\frac{144-25}{169}$
$latex \cos(2A)=\frac{119}{169}$
EXAMPLE 3
What is the value of $latex \cos(2A)$ if we have $latex \sin(A) = \frac{2}{9}$?
Solution
In this exercise, we only have the value of the sine of A, but we can find the value of the cosine of the double angle A by using the third variation of the double angle formula for the cosine. Therefore, we have:
$latex \cos(2A)=1-2{{\sin}^2}(A)$
$latex \cos(2A)=1-2{{(\frac{2}{9})}^2}$
$latex \cos(2A)=1-2(\frac{4}{81})$
$latex \cos(2A)=1-\frac{8}{81}$
$latex \cos(2A)=\frac{73}{81}$
EXAMPLE 4
Find an expression for $latex \cos (4A)$.
Solution
We can write $latex \cos(4A)$ as $latex \cos(2A+2A)$. Now, we can use the identity of the double angle for cosine, where the angle is 2A. Therefore, we have:
$$\cos(2A+2A)=\cos(2A)\cos(2A)-\sin(2A)\sin(2A)$$
$latex ={{\cos}^2}(2A)-{{\sin}^2}(2A)$
Now, we use the double angle identities for both cosine and sine. In the case of the sine, we use the second variation:
$$\cos(4A)={{\cos}^2}(2A)-{{\sin}^2}(2A)$$
$$={{(2{{\cos}^2}(A)-1)}^2}-{{(2\sin(A)\cos(A))}^2}$$
$$=4{{\cos}^4}(A)-4{{\cos}^2}(A)+1-4{{\sin}^2}(A){{\cos}^2}(A)$$
$$=4{{\cos}^4}(A)-4{{\cos}^2}(A)+1 -4(1-{{\cos}^2}(A)){{\cos}^2}(A)$$
$$=4{{\cos}^4}(A)-4{{\cos}^2}(A)+1 -4{{\cos}^2}(A)+4{{\cos}^4}(A)$$
$latex =8{{\cos}^4}(A)-8{{\cos}^2}(A)+1$
Double angle identities – Practice problems
Use the following problems to practice using the double-angle identities seen above. If you need help with this, you can look at the solved examples.
See also
Interested in learning more about trigonometric identities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
