The unit circle is used in mathematics to relate to basic trigonometric functions in an easier way. Since the radius of the unit circle is 1, this makes it easier to apply the Pythagorean theorem and results in the x-coordinates being equivalent to the cosine and the y-coordinates being equivalent to the sine.
Here, we will learn more details about the unit circle using diagrams. We will learn the values of the sine and cosine functions of the most important angles in terms of radians.
TRIGONOMETRY
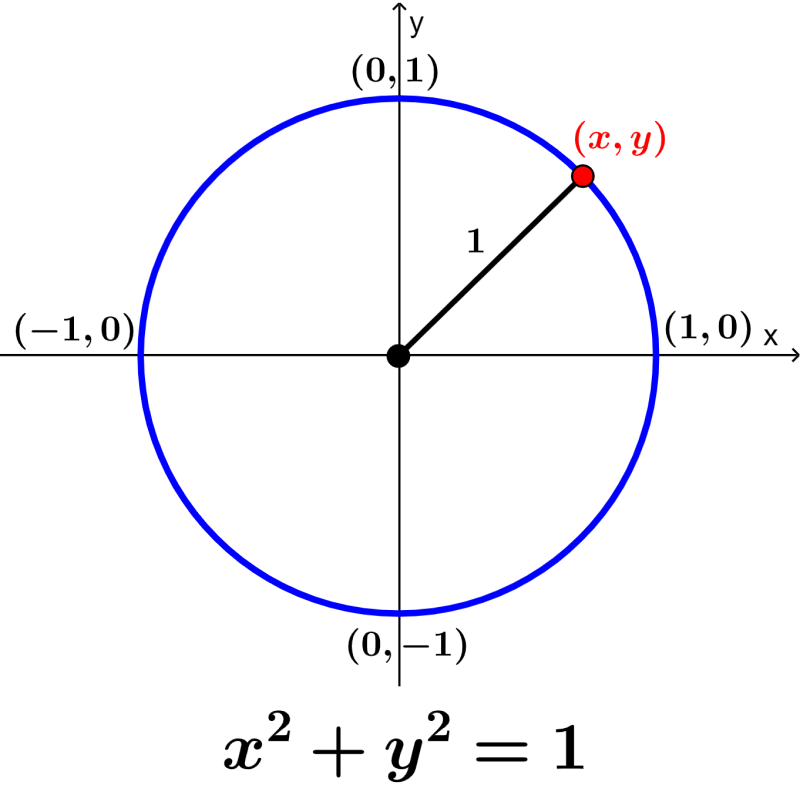
Relevant for…
Learning about the unit circle with examples and diagrams.
TRIGONOMETRY
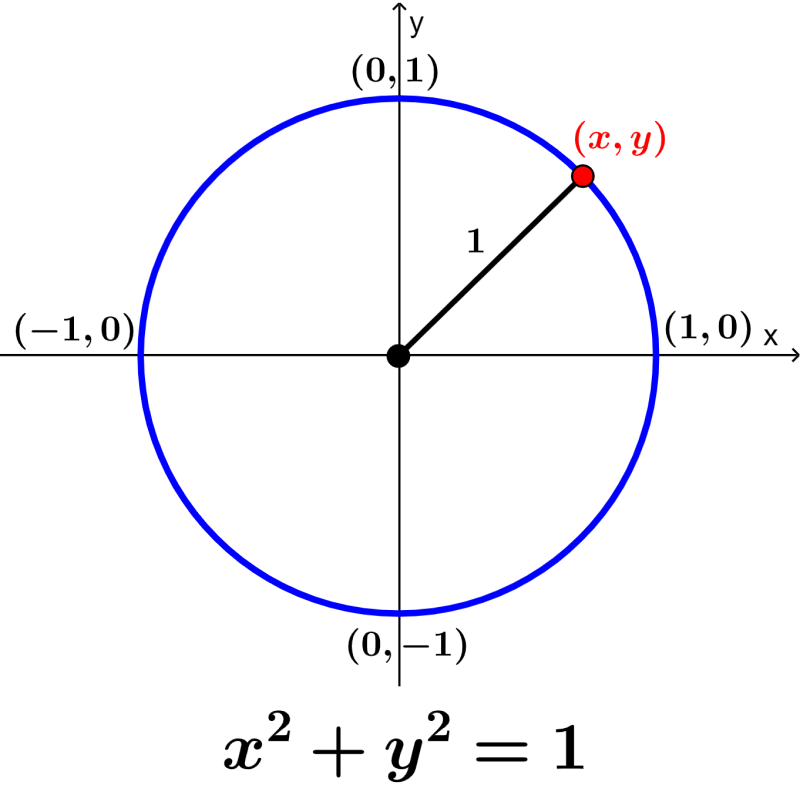
Relevant for…
Learning about the unit circle with examples and diagrams.
What is the unit circle?
A unit circle is a circle that has a radius of 1. For example, the following image shows a unit circle.
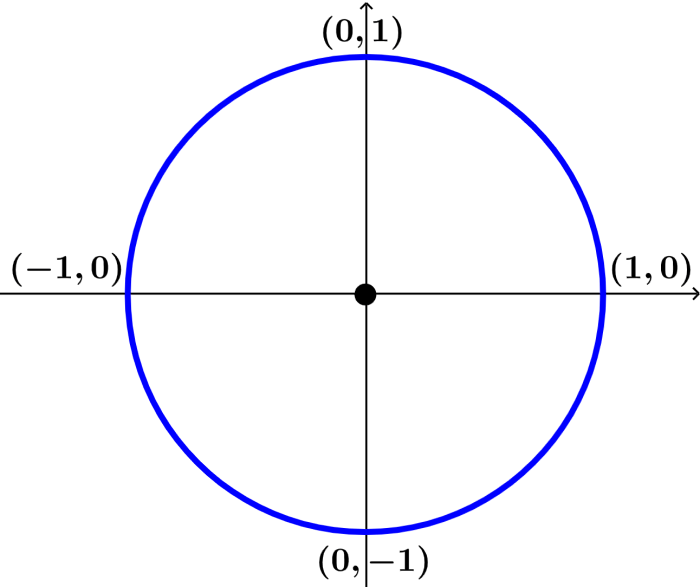
The unit circle is used in mathematics to understand the relationships of the different trigonometric functions in the Cartesian plane. In this circle, the values of the sine of an angle are equivalent to the y-coordinates and the values of the cosine of an angle are equivalent to the x-coordinates.
Using the Pythagorean theorem on the unit circle, we can relate the trigonometric functions sine, cosine, and tangent.
Formula for the unit circle
The equation of a circle is given by the general form:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
where, $latex (h, k)$ are the coordinates of the center of the circle and r is the radius. Therefore, $latex (x, y)$ represents the points on the circle that are located at a distance r from the center.
In the case of the unit circle, the center is located at (0, 0) and the radius is 1. This means that the formula for the unit circle is:
$latex {{x}^2}+{{y}^2}=1$
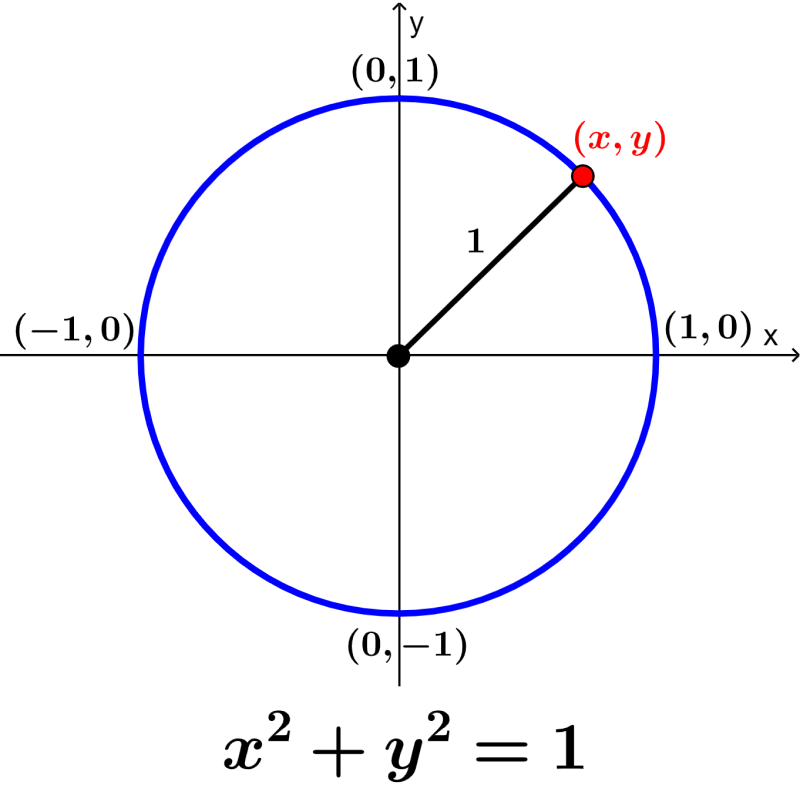
Calculate trigonometric functions using the unit circle
We can calculate the trigonometric functions using the unit circle. For this, we have to apply the Pythagorean theorem in a unit circle to relate to the trigonometric functions. In the following diagram, we have the trigonometric functions graphed on a unit circle in the Cartesian plane.
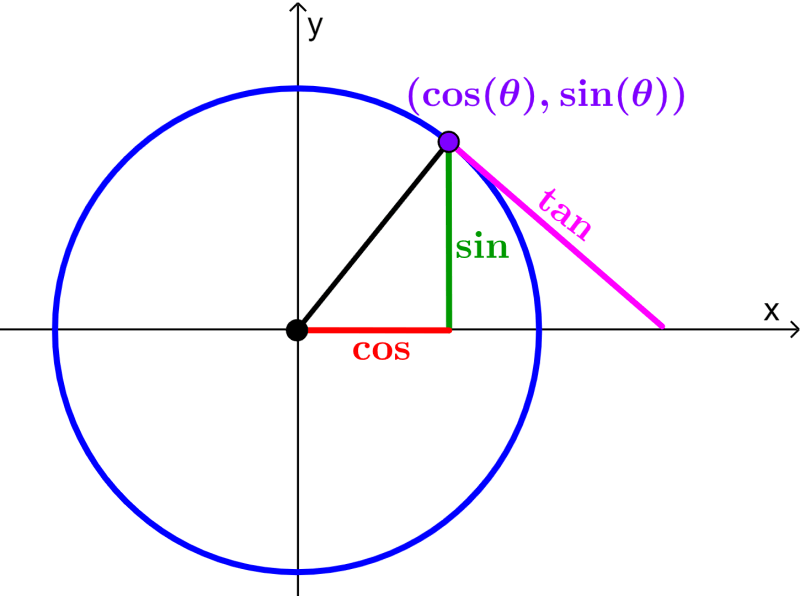
In the unit circle, the cosine is equivalent to the x-coordinate and the sine is equivalent to the y-coordinate. For example, let’s see what happens when $latex \theta=0$.
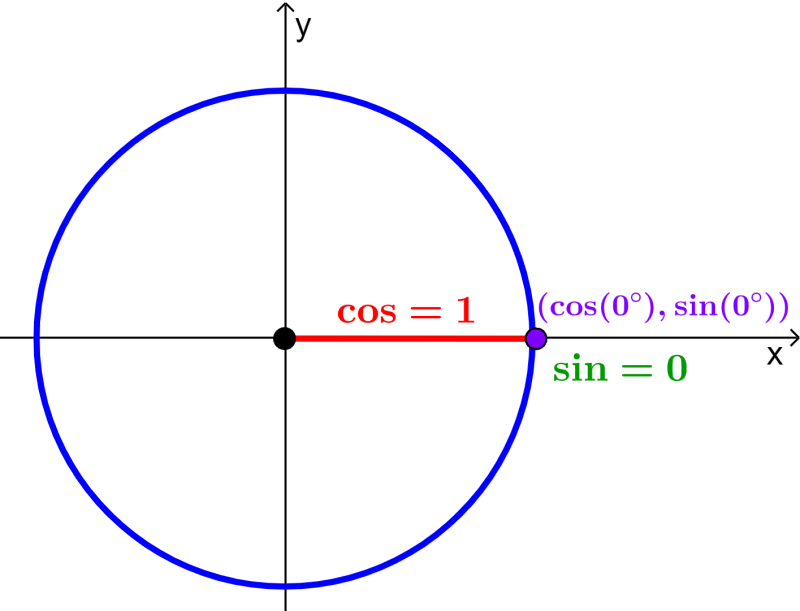
We observe that the coordinate in x is 1 and the coordinate in y is 0, so we have:
- $latex \cos(0)=1$
- $latex \sin(0)=0$
Now, let’s see what happens when $latex \theta=90°$.
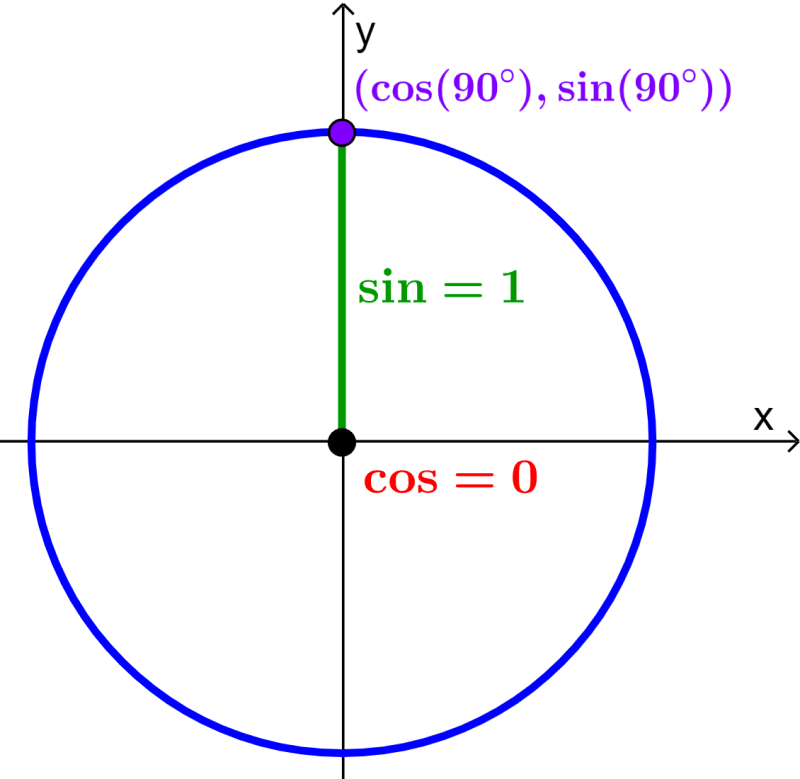
In this case, we observe that the x-coordinate is 0 and the y-coordinate is 1, so we have:
- $latex \cos(90) = 0$
- $latex \sin(90)=1$
This can be extended to various angles by considering the proportions of the x-coordinate and the y-coordinate.
The unit circle in radians
Many times, measuring at angles in radians is more useful, especially in topics related to Calculus. For this reason, we are going to find various values in the unit circle using radians. Recall that one complete turn of the unit circle is equal to 360°, which is equal to 2π radians.
We can convert the angles to radians and express in terms of radians:
| Angle | Radians | Sine | Cosine |
| 0° | 0 | 0 | 1 |
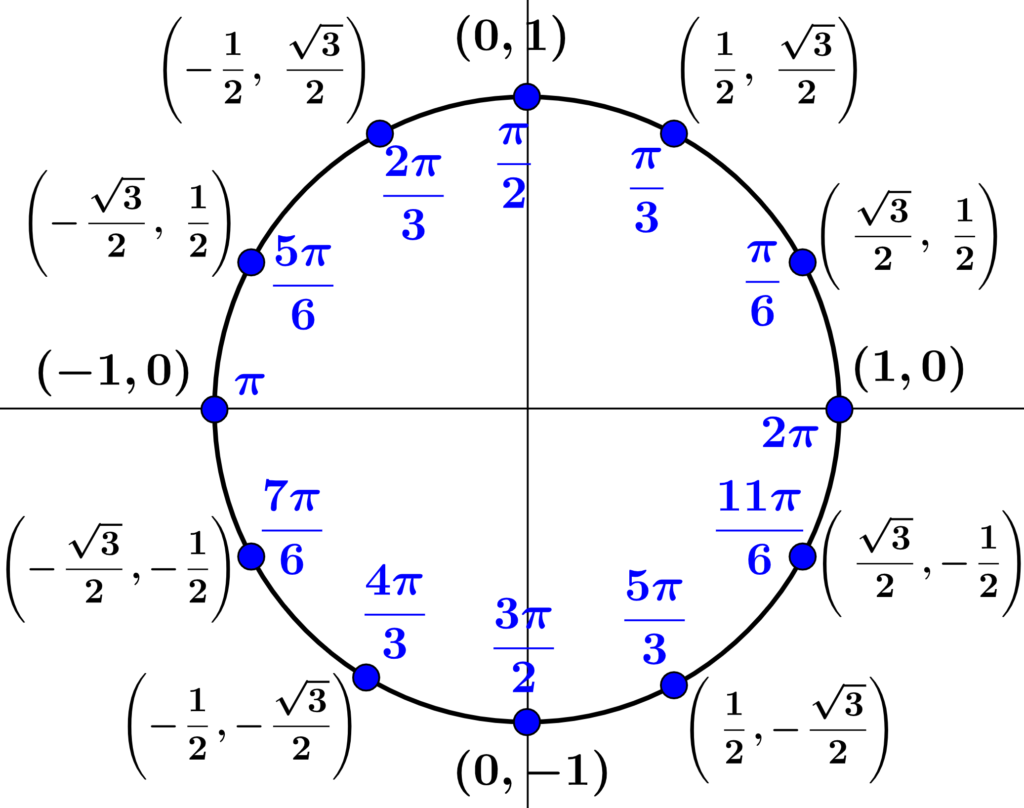
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{1}{2}$ | $latex \frac{\sqrt{3}}{2}$ |
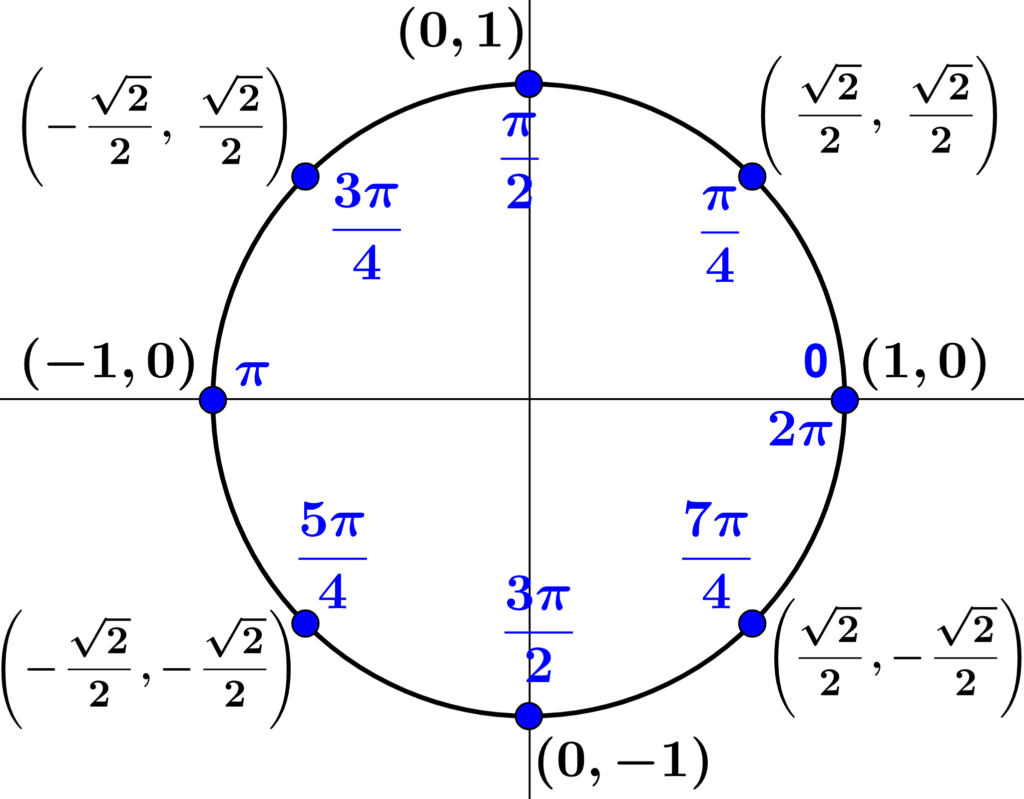
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{\sqrt{2}}{2}$ |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{2}$ |
| 90° | $latex \frac{\pi}{2}$ | 1 | 0 |
These are the values of the trigonometric functions in the first quadrant of the unit circle. The numbers $latex \frac{1}{2}$, $latex \frac{\sqrt{2}}{2}$, $latex \frac{\sqrt{3}}{2}$, 0 and 1 are repeated taking into account the signs of the 4 quadrants:
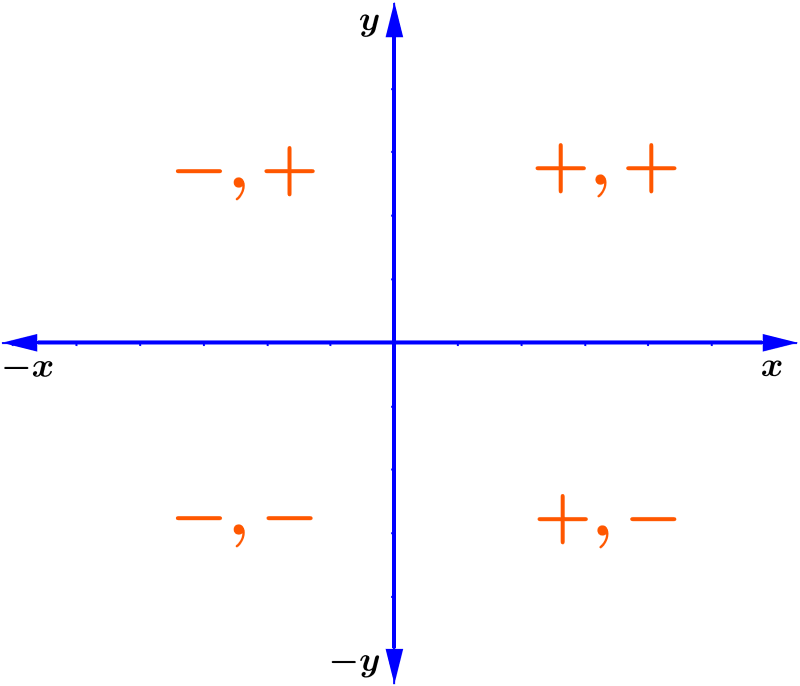
Therefore, the following diagrams represent the unit circle with the values of the trigonometric functions of the most important angles.
See also
Interested in learning more about tangent of an angle? Take a look at these pages:



