The graph of the tangent looks different compared to the graphs of the sine and cosine. Unlike the domain of the sine and cosine, the domain of the tangent is not equal to all real numbers. The tangent is equivalent to the sine over the cosine. Therefore, when the cosine values are equal to 0, the tangent goes to infinity. This means that the tangent has asymptotes when the cosine values are 0. On the other hand, the range of the tangent is equal to all real numbers.
Here, we will learn how to graph the basic tangent function and we will learn about the variations we can make to modify its graph.
TRIGONOMETRY
Relevant for…
Learning about the graph of the tangent function with examples.
TRIGONOMETRY
Relevant for…
Learning about the graph of the tangent function with examples.
Graph of the basic tangent function
Recall that we can write the tangent in terms of the sine and cosine: $latex \tan(x)=\frac{\sin(x)}{\cos(x)}$. This means that the tangent will be equal to zero when the numerator (the sine) is equal to zero. This happens at 0, π, 2π, 3π, etc, and at -π, -2π, -3π, etc.
The tangent will be undefined whenever the denominator (the cosine) is zero. A zero in the denominator means that we have a vertical asymptote. Therefore, the graph of the tangent will have vertical asymptotes every time the cosine is zero: at -π/2, π/2, 3π/2, etc.
Then we can use a value found on each portion of the x-axis to determine the position of the graph. The graph is drawn taking into account that it never crosses the asymptotes.
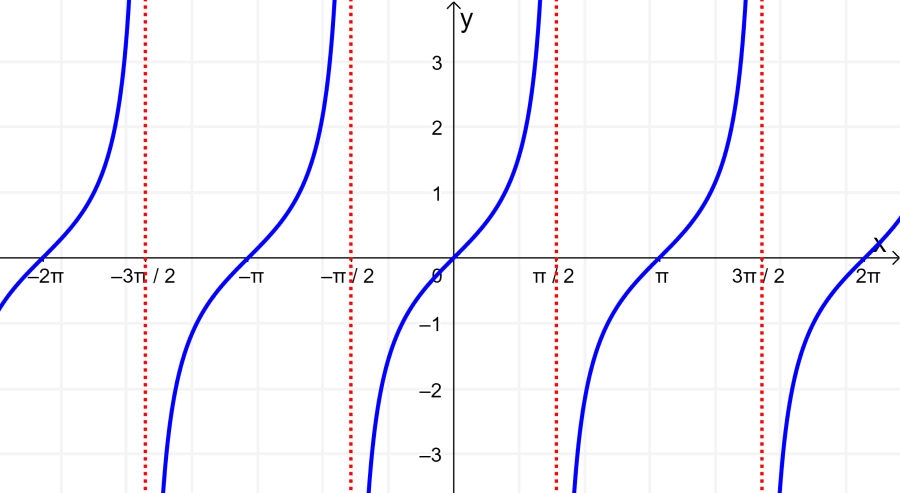
In the graph, we see that the function repeats at regular intervals of π. This means that the period of the tangent is π.
Domain of the tangent function
The tangent function has a pattern that repeats indefinitely to both the positive x side and the negative x side. However, the tangent can be written as $latex \tan(x)= \frac{\sin(x)}{\cos(x)}$ and we know that we cannot have zero in the denominator, so each time we have $latex \cos(x)= 0$, the function is undefined.
This happens when we have multiples of $latex \frac{\pi}{2}$. Therefore, the domain is all real numbers except the multiples of $latex \frac{\pi}{2}$.
Range of the tangent function
The graph of the tangent function clearly shows us that the function can result in any value of y. This means that the range is equal to all real numbers.
Graphs of variations of the tangent function
The graph of the basic tangent function can be modified to obtain different variations. We can modify it by changing the different parameters of the general shape of the tangent. The general form of the tangent function is:
$latex y=A~\tan(Bx-C)+D$
Each of the parameters of the tangent function affects different characteristics of the resulting graph.
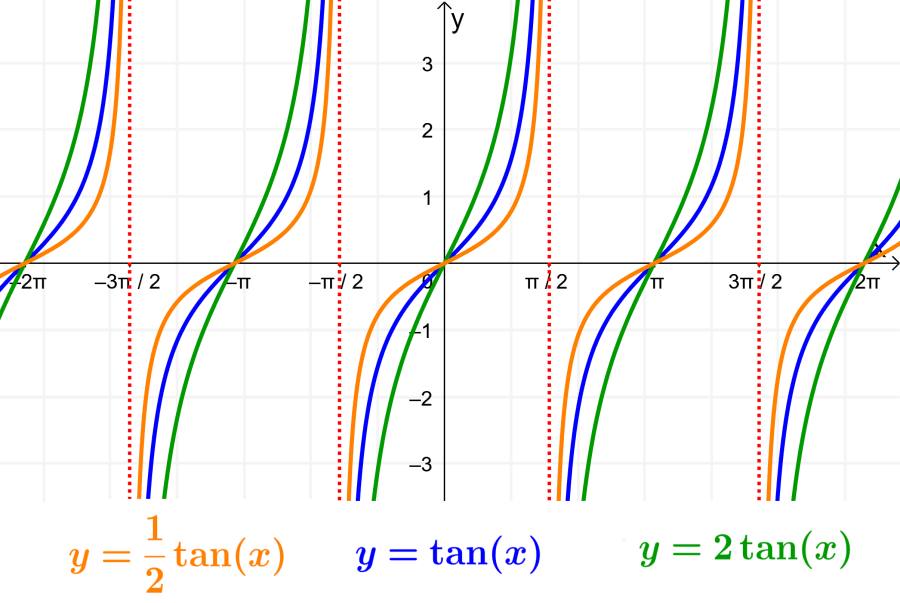
Determining the vertical stretch of the tangent function
The vertical stretch represents the change in the y values of the function with respect to the original function. Using the general form of the tangent, the factor by which the function is stretched vertically is found using |A|. If A is greater than 1, the graph is stretched and if A is between 0 and 1, the graph is compressed.
Determining the period of the tangent function
The period of the tangent function represents the interval after which the function repeats. The period of the basic tangent function is π.
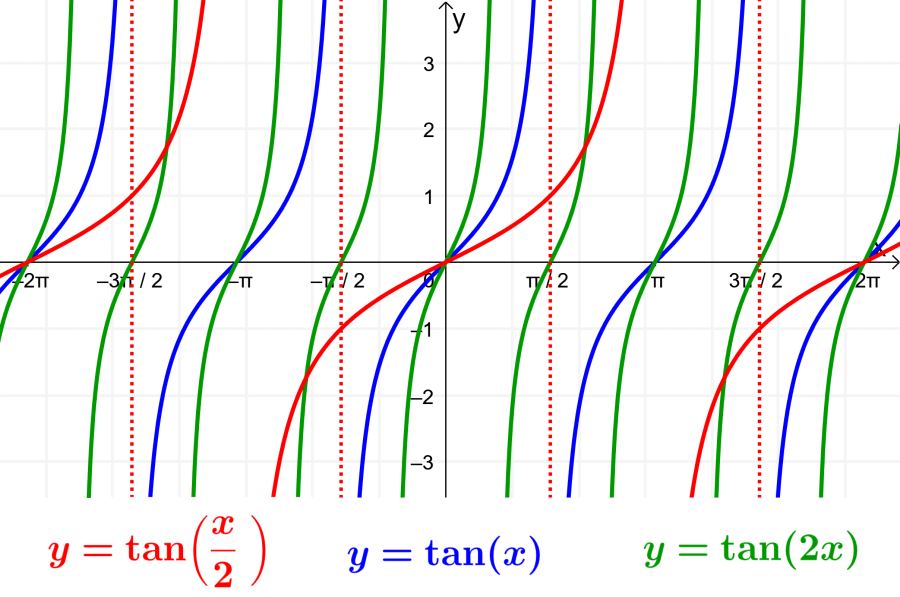
The parameter B in the general form affects the period of the function. We can determine the period using the equation $latex P = \frac{\pi}{|B|}$. When the value of B is greater than 1, the function is “accelerated” and the period is less than π, so the function is horizontally compressed. When the value of B is less than 1, the function is “decelerated” and the period is greater than π, so the function is stretched horizontally.
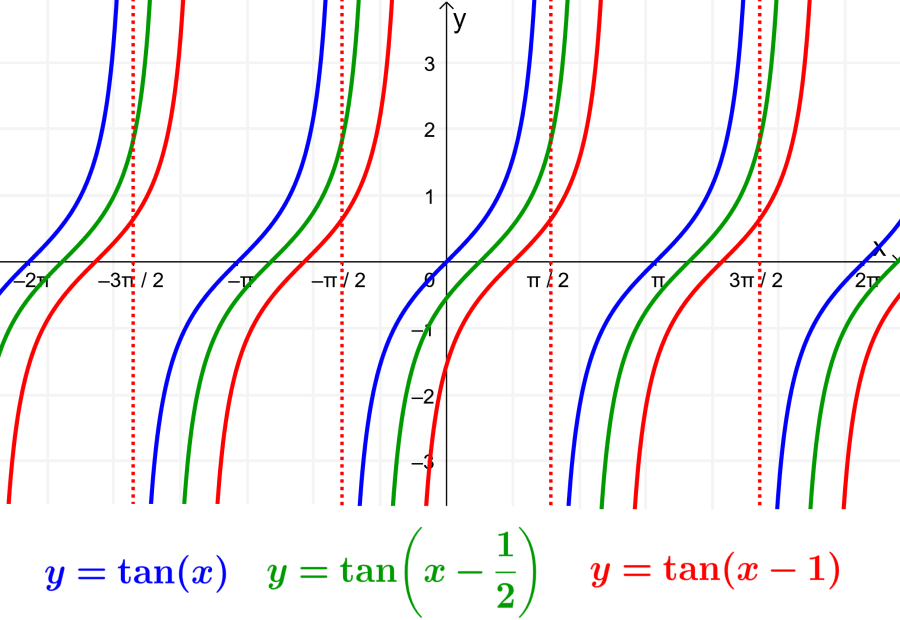
Determining the phase of the tangent function
The phase represents the horizontal displacement of the function with respect to the basic tangent function.
To determine the phase of the function, we rewrite the general form of the function as follows: $latex y = A ~ \tan(B(x- \frac{C}{B})+D$. In this form, the phase equals $latex \frac{C}{B}$. The graph is shifted to the right when $latex C> 0$. The graph is shifted to the left when $latex C<0$.
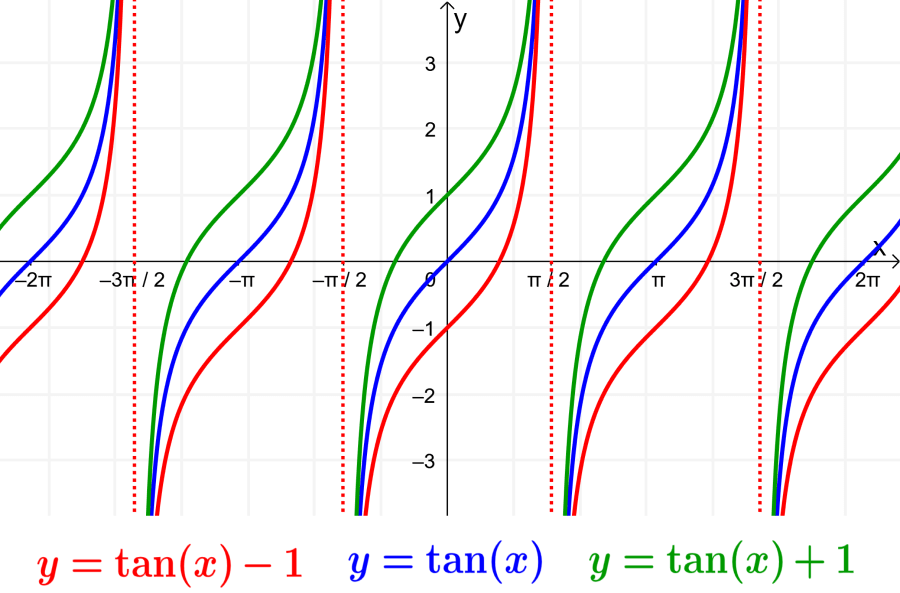
Determining the vertical displacement of the tangent function
The vertical displacement is determined by the value of D in the general form of the tangent function. If we have a positive value of D, the graph is shifted up. If we have a negative value of D, the graph is shifted down.
Examples with answers of the graph of tangent
The following exercises are solved using what has been learned about the graphs of tangents and their different parameters. Try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
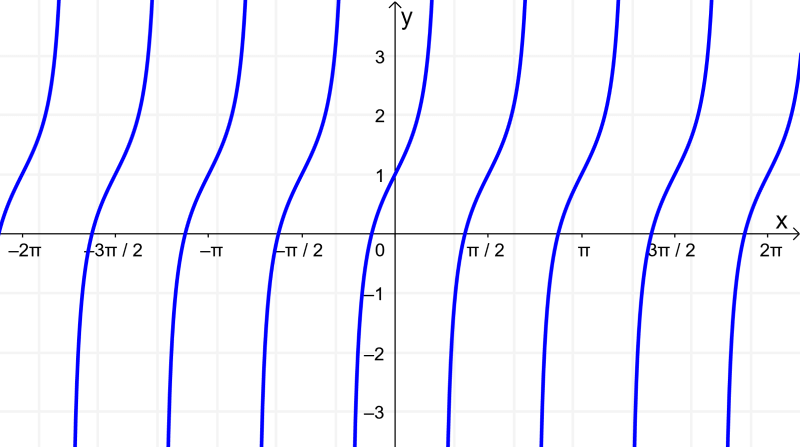
What is the graph of the function $latex y= \tan(2x) +1$?
Solution
To graph this function, we can compare it with the general form to obtain the different parameters and the effects they will have on the graph of the basic tangent function:
- Vertical stretch: $latex |A|=1$. The basic graph is not affected.
- Period: $latex P=\frac{\pi}{|B|}= \frac{\pi}{2}$. The period is half of the basic graph. This means that the graph will be horizontally compressed.
- Phase: $latex \frac{C}{B}=0$. The function is not horizontally shifted.
- Vertical translation: $latex D=1$. The graph is vertically shifted by 1 unit.
Using this, we can obtain the graph of the function:
EXAMPLE 2
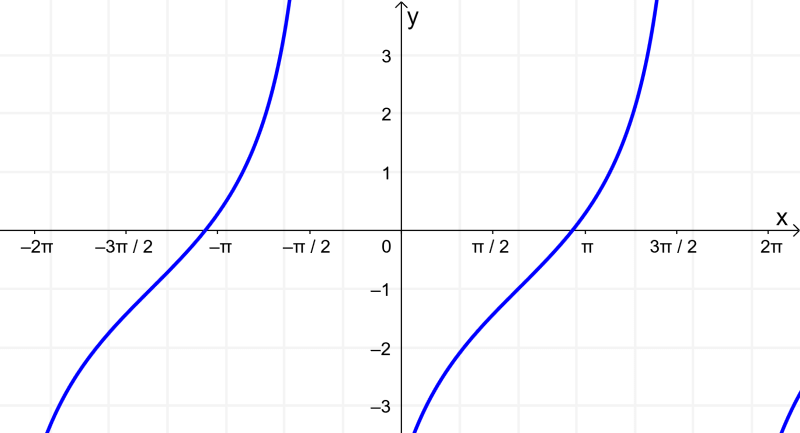
If we have the function $latex y = 2 \tan(\frac{1}{2} x-1) -1$, what is its graph?
Solution
We can use the general form to obtain the different parameters and the following information:
- Vertical stretch: $latex |A|=2$. The graph is stretched vertically by a factor of 2.
- Period: $latex P=\frac{\pi}{|B|}=\frac{\pi}{\frac{1}{2}}=2 \pi$. That’s twice the period of the basic function, so the graph will be stretched horizontally.
- Phase: $latex \frac{C}{B}=\frac{1}{\frac{1}{2}}=2$. The graph is moved 2 units to the right.
- Vertical translation: $latex D=-1$. The graph is shifted 1 unit down.
Applying these transformations to the basic tangent function, we have:
EXAMPLE 3
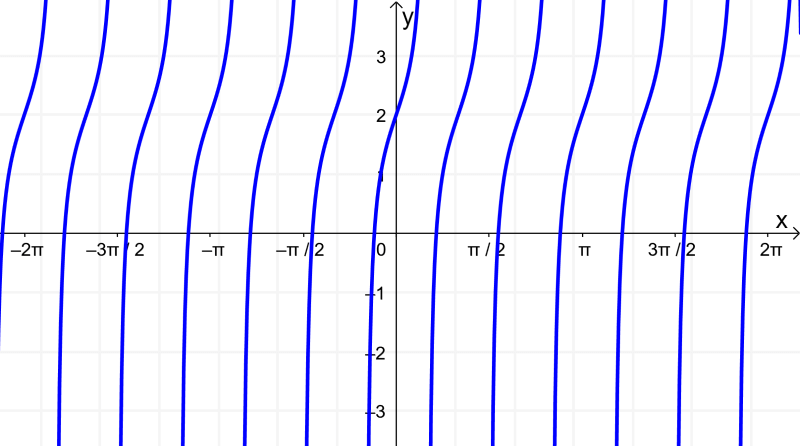
What is the equation of the following tangent function?
Solution
We can extract the following information from the graph:
- The graph is not stretched or compressed vertically. This means that $latex A=1$.
- The graph has a period of $latex \frac{\pi}{3}$. Therefore, the parameter B must be 3.
- The graph does not have any horizontal displacement, so C must be 0.
- The graph is shifted 2 units up, so D equals 2.
We can determine that the equation of this graph is:
$latex y= \tan(3x)+2$
EXAMPLE 4
What is the equation of the following tangent function?
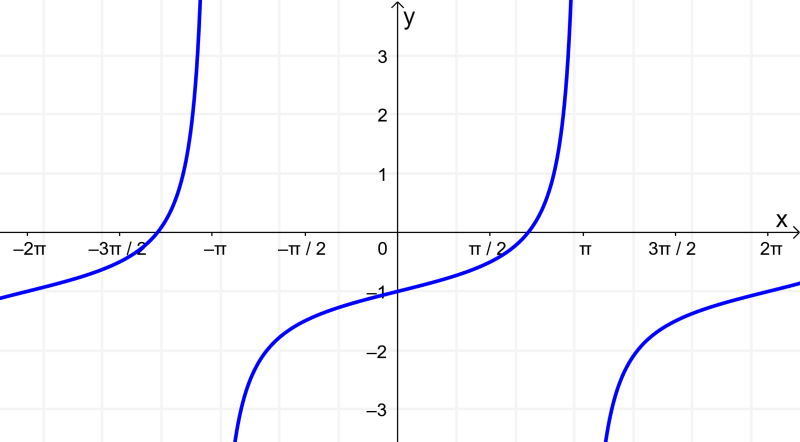
Solution
We can obtain the following information by looking at the graph of the function:
- The graph is vertically compressed. Comparing with the basic tangent function, the y values are half, so $latex A = \frac{1}{2}$.
- The period of the function is 2π, so we have $latex B = \frac{1}{2}$.
- We don’t have any horizontal displacement, so C must be 0.
- The graph is shifted down 1 unit, so D equals -1.
Using this, we conclude that the equation of the graph is:
$latex y = \frac{1}{2} \tan(\frac{1}{2} x) -1$
See also
Interested in learning more about tangent of an angle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
