An inverse function is a function that reverses the effect of the original function. The inverse tangent is a function that reverses the effect of the tangent function. We know that with the tangent function, we can calculate the opposite side if we know the adjacent side and the angle of a right triangle. With the inverse tangent function, we can find the measure of an angle if we know the measures of the opposite side and the adjacent side.
Here, we will learn to use the inverse tangent function and apply it to solve some practice exercises.
How to find the inverse tangent?
To find the inverse tangent, we have to find the angle that would result in the desired number if we obtain its tangent. For example, if we want to find the inverse tangent of 1, we have to ask ourselves “what angle has a tangent of 1?” The answer is 45°, so we conclude that the inverse tangent of 1 is 45°.
We use the notation $latex {{\tan}^{-1}}$ to represent the inverse tangent. Note that in this case, the “-1” does not indicate a reciprocal, but rather indicates that the function is inverse. Using this notation, we would have $latex {{\tan}^{-1}}(1)=45°$.
Actually, there are more angles that have a tangent equal to 1. However, what we are asking is “what is the simplest angle that has a tangent equal to 1?” The answer is 45°. Therefore, we have $latex {{\tan}^{- 1}}(1)=45°$ or in radians, we have $latex {{\tan}^{- 1}}(1) = \frac{\pi}{4}$.
The inverse tangent function is also known as the arctangent function and we can use the notation “arctan(x)” to represent it.
Graph of the inverse tangent function
An inverse function is characterized by the fact that the x-coordinates and the y-coordinates of the function are interchanged. This means that in the inverse tangent function, the x values correspond to the y values of the tangent function and the y values correspond to the x values.
The domain of the inverse tangent function is equal to all real numbers. This means that we can use any number in the input or independent variable (usually x).
The range of the inverse tangent function is equal to all real numbers within $latex -{{90}^{\circ}}<y<{{90}^{\circ}}$ or in radians, $latex – \frac{\pi}{2}< y <\frac{\pi}{2}$. This means that the resulting angle of the inverse tangent has to be within this range.
Examples with answers of inverse tangents
The following exercises can be used to learn about the applications of the inverse tangent. Each exercise has its respective solution, but try to solve the exercises yourself before looking at the answer.
EXAMPLE 1
Use the sides of the triangle and a calculator to find the measure of angle ∠A.
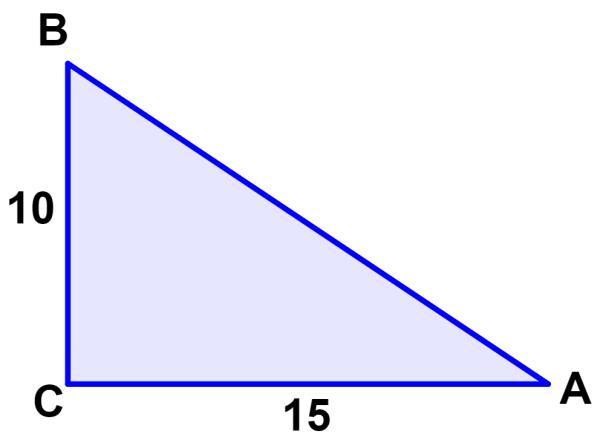
Solution
We can see that in reference to the angle ∠A, we have the measurements of the opposite side and the adjacent side. Therefore, we can form a relationship with the tangent:
$latex \tan(A)=\frac{\text{opposite}}{\text{adjacent}}$
$latex \tan(A)=\frac{10}{15}$
If we use the inverse tangent function, we can write:
$latex {{\tan}^{-1}}(\frac{10}{15})=A$
$latex A=33.7$°
Angle A measures 33.7°.
EXAMPLE 2
What is the value of angle A in the triangle below?
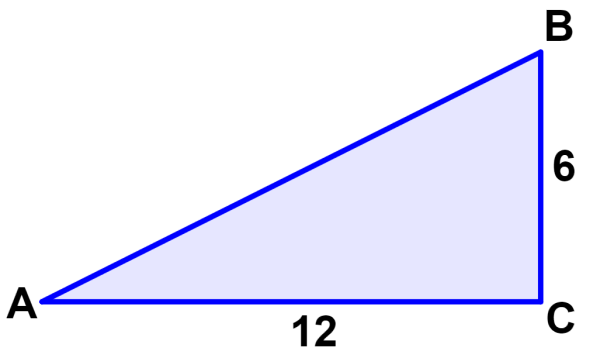
Solution
With respect to the angle ∠A, we know the opposite side and the adjacent side, so we use the tangent to form the following equation:
$latex \tan(A)=\frac{\text{opposite}}{\text{adjacent}}$
$latex \tan(A)=\frac{6}{12}$
Using the inverse tangent function and a calculator, we have:
$latex {{\tan}^{-1}}(\frac{6}{12})=A$
$latex A=26.6$°
Angle A measures 26.6°.
EXAMPLE 3
What is the measure of angle B?
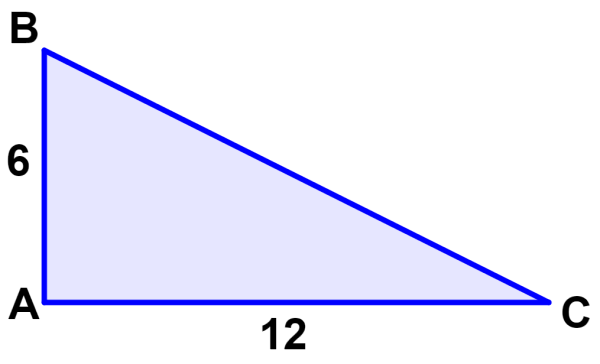
Solution
In reference to the angle ∠B, we have the lengths of the opposite side and the adjacent side, so we use the tangent to find the following relationship:
$latex \tan(B)=\frac{\text{opposite}}{\text{adjacent}}$
$latex \tan(B)=\frac{12}{6}$
Now, we use the inverse tangent to obtain the following using a calculator:
$latex {{\tan}^{-1}}(\frac{12}{6})=B$
$latex B=63.4$°
Angle B measures 63.4°.
See also
Interested in learning more about tangent of an angle? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
