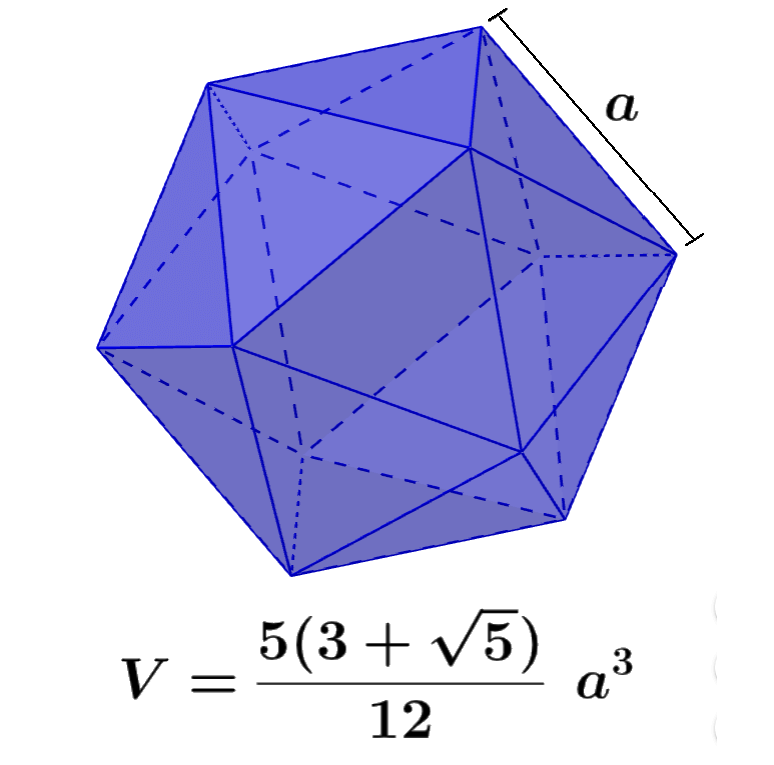
The icosahedron is one of the five Platonic solids. To calculate its volume, we can use the length of one of its sides in a standard formula. On the other hand, its surface area is calculated by adding up the areas of all the triangular faces.
Here, we will learn how to calculate the volume and the surface area of an icosahedron. We will look at how to obtain its formulas, and we will apply them to solve some practice problems.
How to find the volume of an icosahedron
The icosahedron is a regular three-dimensional figure, so all its faces have the same shape and the same dimensions. Therefore, we can calculate the volume of an icosahedron using the length of one of its sides in the following formula:
| $$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$ |
where a is the length of one of the sides of the icosahedron.
Alternatively, we can simplify this equation by getting an approximation for the fraction on the right-hand side of the equation. Thus, we have:
$latex V=2.1817{{a}^3}$
How to find the surface area of an icosahedron
We can use the following formula to determine the surface area of an icosahedron:
| $latex A_{s}=5\sqrt{3}~{{a}^2}$ |
where a is the length of one of the sides of the icosahedron.

This formula can be simplified as follows:
$latex A_{s}\approx 8.66{{a}^2}$
Proof of the formula for the surface area of an icosahedron
We can prove the formula for the surface area of an icosahedron by considering that icosahedrons are regular three-dimensional figures that have all of their sides and all of their faces with the same dimensions.
Therefore, we can calculate the surface area of an icosahedron by finding the area of one of the triangular faces and multiplying the result by 20.
The faces are equilateral triangles and the Area of an Equilateral Triangle can be found with the following formula:
$$A=\frac{\sqrt{3}}{4}~a^2$$
Multiplying that formula by 20, we have:
$$A_{s}=20\times \frac{\sqrt{3}}{4}~a^2$$
$$A_{s}=5\sqrt{3}~a^2$$
Volume and area of an icosahedron – Examples with answers
EXAMPLE 1
Find the volume of an icosahedron that has sides with a length of 2 ft.
Solution
To solve this problem, we are going to use the icosahedron formula with a=2. Therefore, we have:
$$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$
$latex V=2.1817{{a}^3}$
$latex V=2.1817\times {{2}^3}$
$latex V=2.1817\times 8$
$latex V=17.45$
The volume of the icosahedron is $latex 17.45~{{ft}^3}$.
EXAMPLE 2
Find the surface area of an icosahedron that has sides with a length of 2 in.
Solution
Let’s apply the formula for the surface area of an icosahedron using the length a=2:
$latex A_{s}=5\sqrt{3}~a^2$
$latex A_{s}=5\sqrt{3}~(2)^2$
$latex A_{s}=5\sqrt{3}~(4)$
$latex A_{s}=34.64$
The surface area of the icosahedron is $latex 34.64~{{in}^2}$.
EXAMPLE 3
What is the volume of an icosahedron that has sides with a length of 4 ft?
Solution
We apply the formula for the volume of an icosahedron using the value a=4:
$$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$
$latex V=2.1817{{a}^3}$
$latex V=2.1817\times {{4}^3}$
$latex V=2.1817\times 64$
$latex V=139.63$
The volume of the icosahedron is $latex 139.63~{{ft}^3}$.
EXAMPLE 4
What is the surface area of an icosahedron that has sides with a length of 5 ft?
Solution
Using the surface area formula with length a=5, we have:
$latex A_{s}=5\sqrt{3}~a^2$
$latex A_{s}=5\sqrt{3}~(5)^2$
$latex A_{s}=5\sqrt{3}~(25)$
$latex A_{s}=216.51$
The surface area of the given icosahedron is $latex 216.51~{{ft}^2}$.
EXAMPLE 5
If an icosahedron has sides with a length of 7 in, what is its volume?
Solution
Using the formula for the volume of an icosahedron with length a=7, we have:
$$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$
$latex V=2.1817{{a}^3}$
$latex V=2.1817\times {{7}^3}$
$latex V=2.1817\times 343$
$latex V=748.32$
The volume of the given icosahedron is $latex 748.32~{{in}^3}$.
EXAMPLE 6
Find the surface area of an icosahedron that has sides with a length of 6 in.
Solution
Applying the surface area formula using a=6, we have:
$latex A_{s}=5\sqrt{3}~a^2$
$latex A_{s}=5\sqrt{3}~(6)^2$
$latex A_{s}=5\sqrt{3}~(36)$
$latex A_{s}=311.77$
The surface area of the icosahedron is $latex 311.77~{{in}^2}$.
EXAMPLE 7
The volume of an icosahedron is $latex 60~{{ft}^3}$. What is the length of one of its sides?
Solution
In this example, we know the volume of the icosahedron and we have to find the length of one of its sides. Therefore, we can use the volume formula and solve for a:
$$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$
$latex V=2.1817{{a}^3}$
$latex 60=2.1817{{a}^3}$
$latex 27.5={{a}^3}$
$latex a=3.02$
The icosahedron has sides with a length of 3.02 ft.
EXAMPLE 8
If an icosahedron has a surface area of $latex 67.9~{{ft}^2}$, determine the length of one of its sides.
Solution
In this case, we already have the surface area of the icosahedron and we need to find the length of one of its sides. Therefore, we can use the surface area formula and solve for a:
$latex A_{s}=5\sqrt{3}~a^2$
$latex 67.9=5\sqrt{3}~a^2$
$latex 7.84={{a}^2}$
$latex a=2.8$
Therefore, the sides of the icosahedron have length of a=2.8 feet.
EXAMPLE 9
Determine the length of the sides of an icosahedron that has a volume of $latex 170~{{in}^3}$.
Solution
Let’s use the volume formula and solve for a:
$$V=\frac{5(3+\sqrt{5})}{12}{{a}^3}$$
$latex V=2.1817{{a}^3}$
$latex 170=2.1817{{a}^3}$
$latex 77.92={{a}^3}$
$latex a=4.27$
The sides of the icosahedron have a length of 4.27 in.
EXAMPLE 10
Find the length of the sides of an icosahedron that has a surface area of $latex 175~{{in}^2}$.
Solution
This example is similar to the previous one, so we need to use the given surface area value and solve for a:
$latex A_{s}=5\sqrt{3}~a^2$
$latex 175=5\sqrt{3}~a^2$
$latex 20.207={{a}^2}$
$latex a=4.495$
The sides of the icosahedron have a length of 4.495 in.
Volume and area of an icosahedron – Practice problems


Find the length of the sides of an icosahedron that has a surface area of 866.03 m2.
Write the answer in the input box.
See also
Interested in learning more about icosahedrons? Take a look at these pages: