A tetrahedron is a regular pyramid that has four triangular faces. This means that we can calculate its volume by multiplying the area of its base by the height of the tetrahedron and dividing by three. Also, its surface area is calculated by adding the areas of the four triangular faces.
Here, we will learn about the formulas to find the volume and surface area of a tetrahedron. We will learn how to derive these formulas, and we will use them to solve some practice exercises.
How to find the volume of a tetrahedron
Since the tetrahedron is a triangular pyramid, we can calculate its area by multiplying the area of its base by the length of its height and dividing by 3.
The formula for the volume of a regular tetrahedron is:
| $latex V=\frac{{{a}^3}\sqrt{2}}{12}$ |
Proof of the formula for the volume of a tetrahedron
As we mentioned earlier, tetrahedra are triangular pyramids. Also, the area of any pyramid can be calculated by multiplying the area of its base by the height of the pyramid and dividing by three. Therefore, we have:
$latex V=\frac{1}{3}A_{b}H$
where, $latex A_{b}$ is the area of the base and H is the height of the tetrahedron.
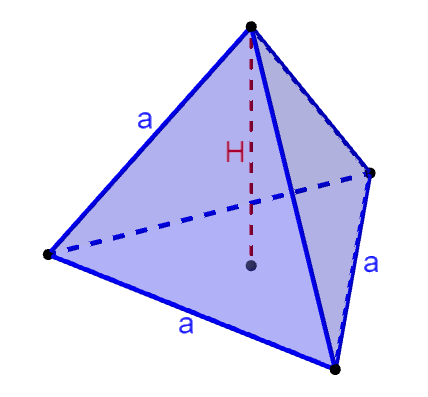
The base of a tetrahedron is an equilateral triangle and we know that the area of any triangle is equal to one-half the base multiplied by the height. Then, we have:
$latex A_{b}=\frac{1}{2}bh$
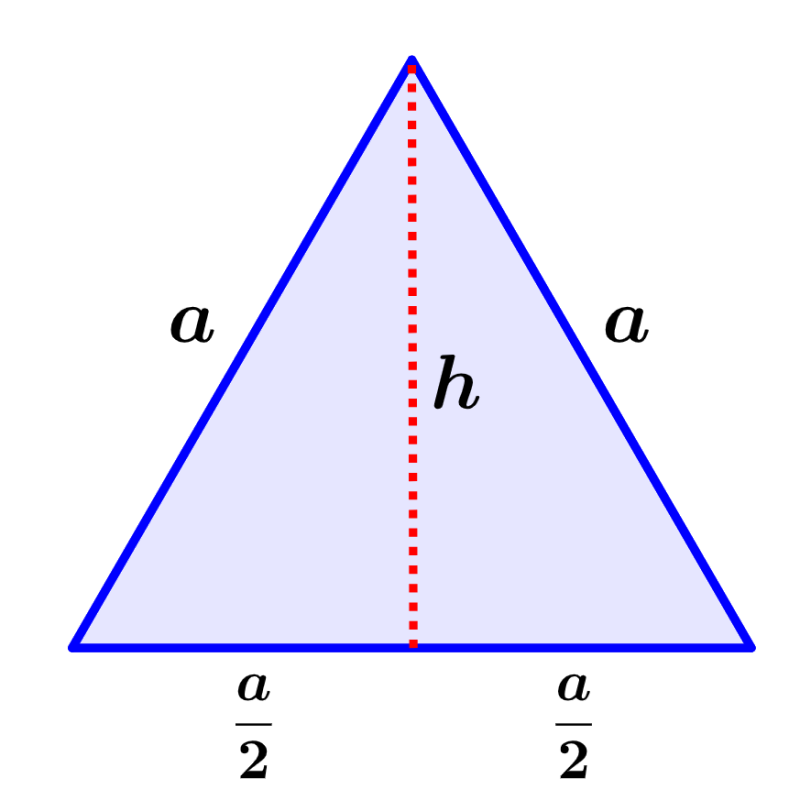
The base of the triangle is equal to one of the sides of the tetrahedron, a. Also, the height of an equilateral triangle is equal to $latex \frac{\sqrt{3}}{2}a$, where a is the length of one of the sides. Therefore, we have
$latex A_{b}=\frac{1}{2}bh$
$latex A_{b}=\frac{1}{2}a\left( \frac{\sqrt{3}}{2}a\right)$
$latex A_{b}=\frac{\sqrt{3}}{4}{{a}^2}$
Finally, we have that the height of a tetrahedron is equal to:
$latex H=\frac{\sqrt{6}}{3}a$
Substituting all this into the formula for the volume of a tetrahedron, we have:
$latex V=\frac{1}{3}A_{b}H$
$latex V=\frac{1}{3}\left(\frac{1}{2}bh\right)\left(\frac{\sqrt{6}}{3}a\right)$
$latex V=\frac{{{a}^3}\sqrt{18}}{36}$
$latex V=\frac{{{a}^3}\sqrt{9\times 2}}{36}$
$latex V=\frac{3{{a}^3}\sqrt{2}}{36}$
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
How to find the surface area of a tetrahedron
Tetrahedra are made up of four congruent faces. This means that we can calculate their surface area by adding the areas of the four faces.
The formula for the surface area of a regular tetrahedron is:
| $latex A_{s}=\sqrt{3} ~{{a}^2}$ |
Proof of the formula for the surface area of a tetrahedron
Since the tetrahedra are triangular pyramids, all four of their faces are congruent. This means that all their faces have the same shape and size. Therefore, we can calculate the surface area if we know the area of one of the faces of the tetrahedron.
This means we have:
$latex A_{s}=4A_{t}$
where, $latex A_{s}$ is the surface area of the tetrahedron and $latex A_{t}$ is the area of one of the triangular faces.
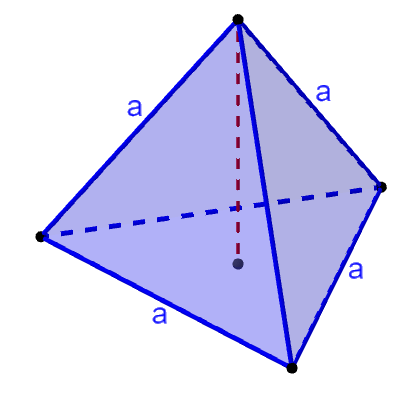
Now, we can calculate the area of one of the faces considering that the faces of a tetrahedron are equilateral triangles. Therefore, we use the formula for the area of an equilateral triangle:
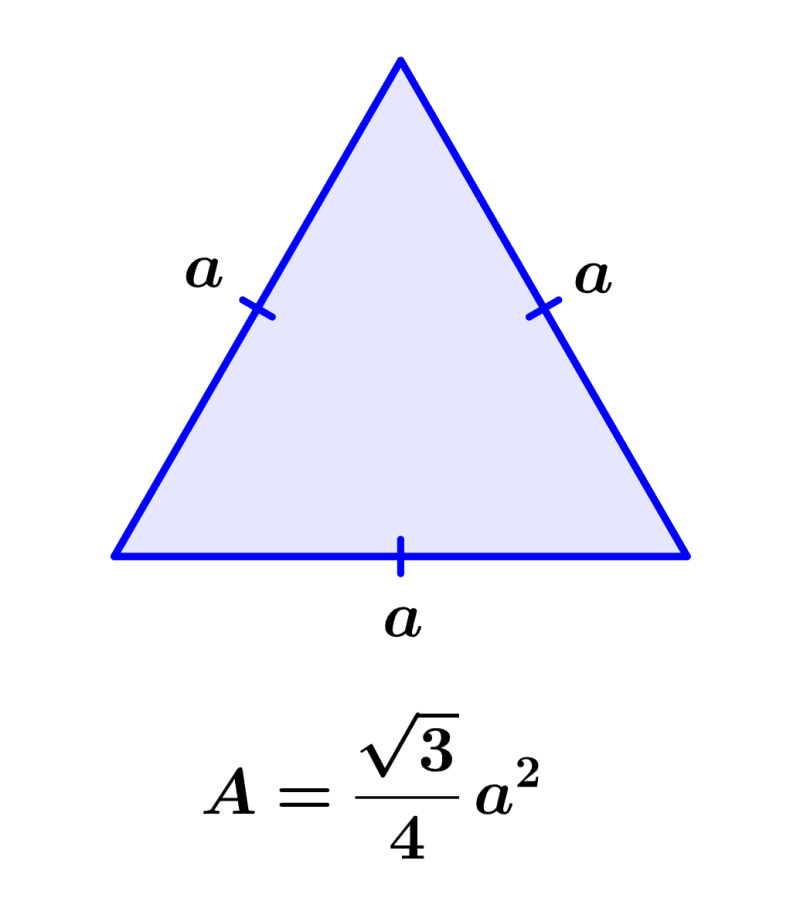
where a is the length of one of the sides.
Substituting this into the tetrahedron surface area formula, we have:
$latex A_{s}=4A_{t}$
$latex A_{s}=4\frac{\sqrt{3}}{4}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{a}^2}$
Volume and area of a tetrahedron – Examples with answers
EXAMPLE 1
If a tetrahedron has sides 3 m long, what is its volume?
Solution
To find the volume of the given tetrahedron, we can simply apply the volume formula by substituting a=3. Therefore, we have:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{3}^3}\sqrt{2}}{12}$
$latex V=\frac{9\sqrt{2}}{12}$
$latex V=1.06$
The volume of the tetrahedron is $latex 1.06 {{m}^3}$.
EXAMPLE 2
What is the surface area of a tetrahedron that has sides with a length of 5 m?
Solution
We are going to use the surface area formula given above by substituting a=5. Then, we have:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{5}^2}$
$latex A_{s}=\sqrt{3}~25$
$latex A_{s}=43.3$
The surface area of the tetrahedron is $latex 43.3 {{m}^2}$.
EXAMPLE 3
A tetrahedron has sides with a length of 20 cm. Calculate its volume.
Solution
We have that a=20. So, we use the formula for the volume of a tetrahedron substituting the given length:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{20}^3}\sqrt{2}}{12}$
$latex V=\frac{8000\sqrt{2}}{12}$
$latex V=942.8$
The volume of the tetrahedron is $latex 942.8 {{cm}^3}$.
EXAMPLE 4
If a tetrahedron has sides 6 m long, what is its surface area?
Solution
Using a=6 in the surface area formula, we have:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{6}^2}$
$latex A_{s}=\sqrt{3}~36$
$latex A_{s}=62.35$
The surface area of the tetrahedron is $latex 62.35 {{m}^2}$.
EXAMPLE 5
What is the volume of a tetrahedron that has sides with a length of 10 m?
Solution
We use the volume formula substituting the value of the length of the sides. Therefore, we have:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex V=\frac{{{10}^3}\sqrt{2}}{12}$
$latex V=\frac{1000\sqrt{2}}{12}$
$latex V=117.9$
The volume of the tetrahedron is $latex 117.9 {{m}^3}$.
EXAMPLE 6
What is the surface area of a tetrahedron that has sides with a length of 12 cm?
Solution
Using the surface area formula with a=12, we have:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex A_{s}=\sqrt{3}~{{12}^2}$
$latex A_{s}=\sqrt{3}~144$
$latex A_{s}=249.4$
The surface area of the tetrahedron is $latex 249.4 {{m}^2}$.
EXAMPLE 7
If the volume of a tetrahedron is equal to $latex 1000 {{m}^3}$, what is the length of its sides?
Solution
In this case, we have the value of the volume and we want to obtain the length of one of its sides. Therefore, we can use the tetrahedron volume formula and solve for a:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 1000=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 12000={{a}^3}\sqrt{2}$
$latex 12000={{a}^3}\sqrt{2}$
$latex 8485.3={{a}^3}$
$latex a=20.4$
So, the sides of the tetrahedron are 20.4 m long.
EXAMPLE 8
If the surface area of a tetrahedron is equal to $latex 300 {{m}^2}$, what is the length of its sides?
Solution
In this case, we have to find the length of one of the sides of the tetrahedron. Then, we can use the surface area formula and solve for a:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex 300=\sqrt{3}~{{a}^2}$
$latex 173.2={{a}^2}$
$latex a=13.16$
The length of one of the sides of the tetrahedron is 16.16 m.
EXAMPLE 9
The volume of a tetrahedron is equal to $latex 400 {{m}^3}$. What is the length of its sides?
Solution
Similar to the previous problem, we are going to use the formula for the volume of a tetrahedron and then solve for a:
$latex V=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 400=\frac{{{a}^3}\sqrt{2}}{12}$
$latex 4800={{a}^3}\sqrt{2}$
$latex 4800={{a}^3}\sqrt{2}$
$latex 3394.1={{a}^3}$
$latex a=15.03$
Therefore, the sides of the tetrahedron measure 15.03 m.
EXAMPLE 10
If the surface area of a tetrahedron is equal to $latex 1000 {{m}^3}$, what is the length of its sides?
Solution
Again, we use the surface area formula and solve for a. Therefore, we have:
$latex A_{s}=\sqrt{3}~{{a}^2}$
$latex 1000=\sqrt{3}~{{a}^2}$
$latex 577.35={{a}^2}$
$latex a=24.03$
The length of the sides of the tetrahedron is 24.03 m.
Volume and area of a tetrahedron – Practice problems


The surface area of a tetrahedron is equal to 180.2 m2, what is the length of its sides?
Write the answer to one decimal place.
See also
Interested in learning more about tetrahedra? Look at these pages:




