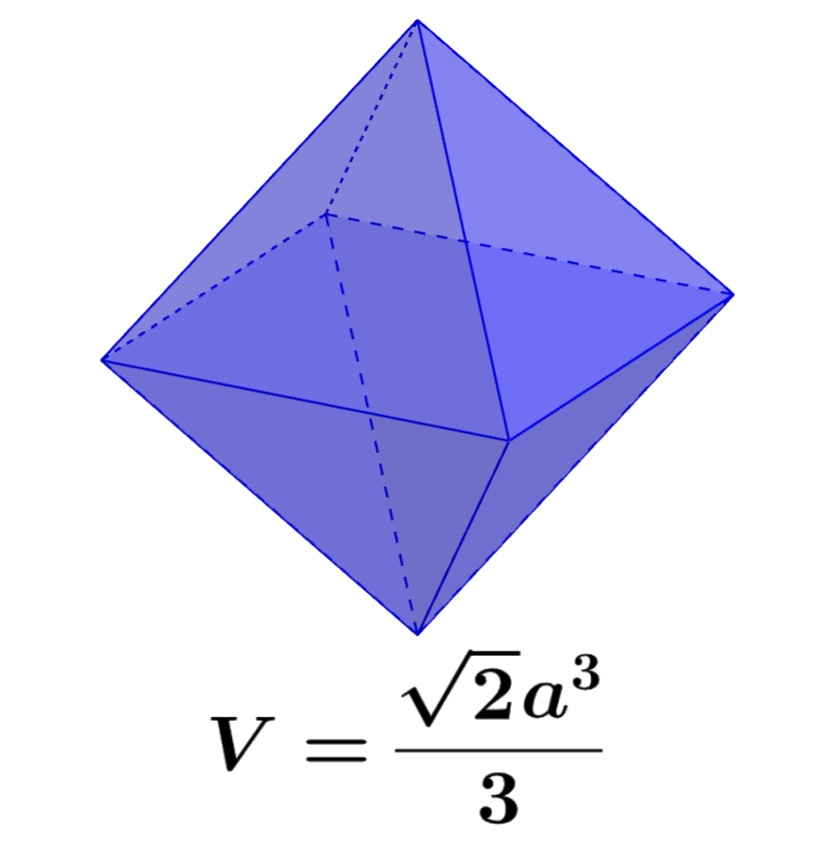An octahedron is a three-dimensional figure formed by joining two pyramids at their bases. We can calculate the volume of an octahedron by adding the volume of the two pyramids that compose it. Also, the surface area is calculated by adding the areas of its eight faces.
In this article, we will look at the formulas that we can use to calculate the volume and surface area of an octahedron. We will learn how to derive these formulas and apply them to solve some problems.
How to find the volume of an octahedron
We can calculate their volume using the following formula:
| $latex V=\frac{\sqrt{2}}{3} {{a}^3}$ |
where, a is the length of one of the sides of the octahedron.
Proof of the formula for the volume of an octahedron
An octahedron can be formed by joining two pyramids at their bases. This means that we can get the volume of an octahedron if we add the volumes of both pyramids.
Since both pyramids are the same, this means we have to find the volume of one pyramid and simply multiply by 2 to get the volume of the octahedron.
Now, to calculate the volume of any pyramid, we can use the following formula:
$latex V_{p}=\frac{A_{b}\times h}{3}$
where, $latex A_{b}$ is the area of the base and h is the height of the pyramid.
In this case, the base of the pyramid is square, so its area is equal to $latex {{a}^2}$.
The height of the pyramid can be calculated using the Pythagorean theorem and the following diagram:
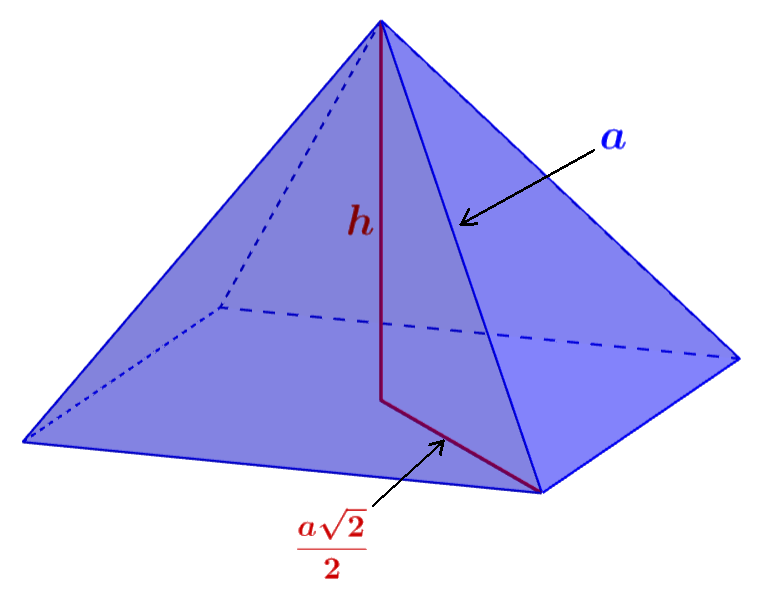
Since the faces of an octahedron are equilateral triangles, all of its sides have a length of a. Therefore, the hypotenuse that we will use is equal to a.
Also, since the diagonal of a square is equal to $latex a\sqrt{2}$, half the diagonal, which is equal to one of the legs, is equal to $latex \frac{a\sqrt{2 }}{2}$.
Therefore, the height of the pyramid is:
$latex h=\sqrt{{{a}^2}-{{(\frac{a\sqrt{2}}{2})}^2}}$
$latex h=\sqrt{{{a}^2}-\frac{{{a}^2}}{2}}$
$latex h=\sqrt{\frac{{{a}^2}}{2}}$
$latex h=\frac{a}{\sqrt{2}}$
$latex h=\frac{a \sqrt{2}}{2}$
Multiplying the height by the area of the base and dividing by 3, we get the volume of the pyramid:
$latex V_{p}=\frac{1}{3}\times{{a}^2}\times \frac{a \sqrt{2}}{2}$
$latex V_{p}=\frac{{{a}^3} \sqrt{2}}{6}$
Multiplying the volume of the pyramid by 2, we get the volume of the octahedron:
$latex V=2\times \frac{{{a}^3} \sqrt{2}}{6}$
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
How to find the surface area of an octahedron
To calculate the surface area of an octahedron, we use the following formula:
| $latex A_{s}=2\sqrt{3}~{{a}^2}$ |
where, a is the length of one of the sides of the octahedron.
Proof of the formula for the surface area of an octahedron
We can obtain the formula for the surface area of an octahedron by considering that the surface area of any three-dimensional figure is equal to the sum of the areas of all its faces.
In the case of octahedrons, we have eight congruent triangular faces. That is, we have eight faces with the same shape and the same dimensions, so the surface area is:
$latex A_{s}=8A_{t}$
where, $latex A_{t}$ is the area of each triangular face.
Also, when we talk about an octahedron, we usually mean a regular octahedron. If this is the case, each triangular face is an equilateral triangle.
Therefore, remembering that the formula for the area of an equilateral triangle is:
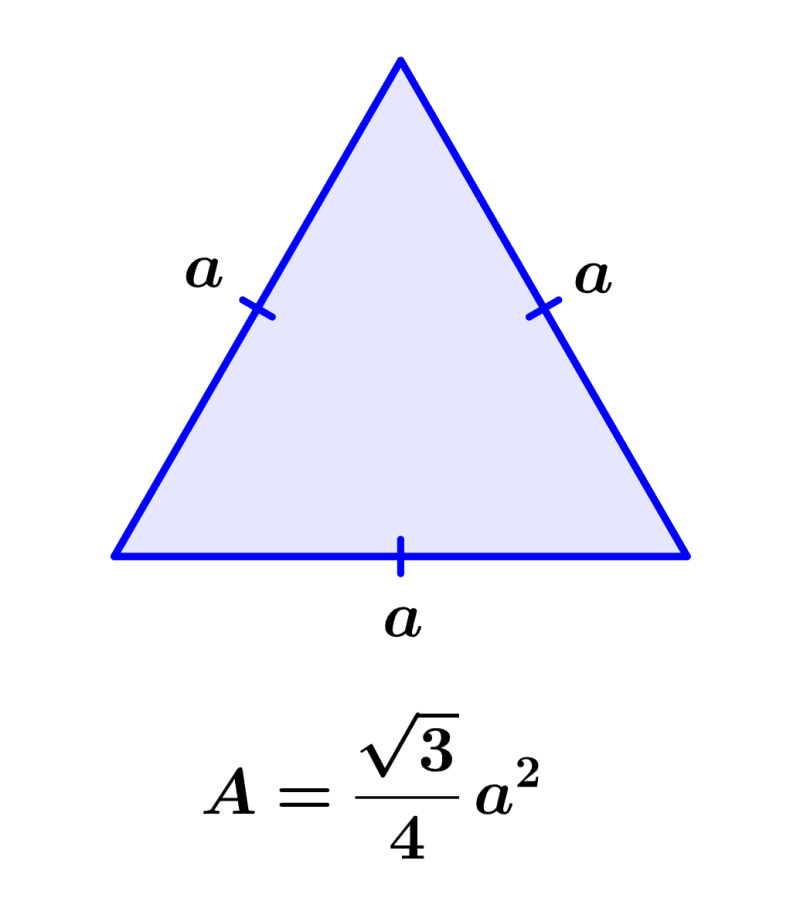
we can substitute that value into the surface area formula:
$latex A_{s}=8\times \frac{\sqrt{3}}{4}{{a}^2}$
$latex A_{s}=2\sqrt{3}~{{a}^2}$
Volume and area of an octahedron – Examples with answers
EXAMPLE 1
If an octahedron has sides 4 m long, what is its volume?
Solution
To solve this problem, we have to use the formula for the volume of an octahedron with the length a=4. So, we have:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{4}^3} \sqrt{2}}{3}$
$latex V=\frac{64 \sqrt{2}}{3}$
$latex V=30.17$
The volume of the octahedron is $latex 30.17 ~{{m}^3}$.
EXAMPLE 2
What is the surface area of an octahedron that has sides with a length of 2 m?
Solution
We can solve this problem by using the formula for the surface area of an octahedron with the value a=2. Therefore, we have:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}\times {{2}^2}$
$latex A_{s}=2\sqrt{3}\times 4$
$latex A_{s}=13.86$
The surface area of the given octahedron is $latex 13.86~{{m}^2}$.
EXAMPLE 3
Calculate the volume of an octahedron that has sides with a length of 5 m.
Solution
Again, we use the formula for the volume of a tetrahedron. In this case, we use the value a=5:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{5}^3} \sqrt{2}}{3}$
$latex V=\frac{125 \sqrt{2}}{3}$
$latex V=58.93$
The volume of the octahedron is $latex 58.93 ~{{m}^3}$.
EXAMPLE 4
Find the surface area of an octahedron that has sides with a length of 5 cm.
Solution
We use the surface area formula, substituting the value a=5. So, we have:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}\times {{5}^2}$
$latex A_{s}=2\sqrt{3}\times 25$
$latex A_{s}=86.6$
Therefore, the surface area is $latex 86.6~{{cm}^2}$.
EXAMPLE 5
If an octahedron has sides 10 cm long, what is its volume?
Solution
We are going to use the formula for the volume of an octahedron using the value a=10. Therefore, we have:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{10}^3} \sqrt{2}}{3}$
$latex V=\frac{1000 \sqrt{2}}{3}$
$latex V=471.4$
Then, the volume of the given tetrahedron is $latex 471.4 ~{{cm}^3}$.
EXAMPLE 6
If an octahedron has sides with a length of 8 cm, what is its surface area?
Solution
We apply the surface area formula with the value a=8:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}\times {{8}^2}$
$latex A_{s}=2\sqrt{3}\times 64$
$latex A_{s}=221.7$
The surface area of the octahedron is $latex 221.7~{{cm}^2}$.
EXAMPLE 7
If the volume of an octahedron is equal to $latex 11.5~{{m}^3}$, what is the length of one of its sides?
Solution
In this case, we know the volume of the octahedron and we want to calculate the length of the sides. Therefore, we use the volume formula and solve for a:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 11.5=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 34.5={{a}^3} \sqrt{2}$
$latex 24.4={{a}^3}$
$latex a=2.9$
The length of one of the sides of the octahedron is 2.9 m.
EXAMPLE 8
If the surface area of an octahedron is $latex 50~{{m}^2}$, what is the length of its sides?
Solution
In this case, we have the surface area of the octahedron and we want to calculate the length of one of its sides. Therefore, we have to use the surface area formula and solve for a:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex 50=2\sqrt{3}~{{a}^2}$
$latex 14.43={{a}^2}$
$latex a=3.8$
The sides of the octahedron have a length of 3.8 m.
EXAMPLE 9
Find the length of the sides of an octahedron that has a volume of $latex 22~{{cm}^3}$.
Solution
To solve this problem, we have to use the formula for the volume of an octahedron and solve for a. Therefore, we have:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 22=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 66={{a}^3} \sqrt{2}$
$latex 46.67={{a}^3}$
$latex a=3.6$
The octahedron has sides with a length of 3.6 cm.
EXAMPLE 10
An octahedron has a surface area of $latex 73.3~{{m}^2}$. Determine the length of one of its sides.
Solution
Let’s use the surface area formula with the given surface area and solve for a:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex 73.3=2\sqrt{3}~{{a}^2}$
$latex 21.16={{a}^2}$
$latex a=4.6$
The octahedron has sides with a length of 4.6 m.
Volume and area of an octahedron – Practice problems


If the surface area of an octahedron is 256.2 cm2, what is the length of its sides?
Write the answer to one decimal place.
See also
Interested in learning more about octahedra? Take a look at theses pages: