Icosahedrons are one of the five Platonic solids. These three-dimensional figures are formed by 20 triangular faces. In total, an icosahedron has 20 faces, 30 edges, and 12 vertices. Each vertex joins five triangular faces.
Here, we will learn more about the faces, vertices, and edges of icosahedrons. We will use diagrams to study these parts of an icosahedron.
Faces of an icosahedron
Icosahedrons have a total of twenty triangular faces. The faces of an icosahedron are the two-dimensional figures that form the outline of the three-dimensional icosahedron.
We can define the faces of an icosahedron as the triangles that are formed by three edges and three vertices. As we can see in the following illustration, each face of the icosahedron connects with five other triangular faces.
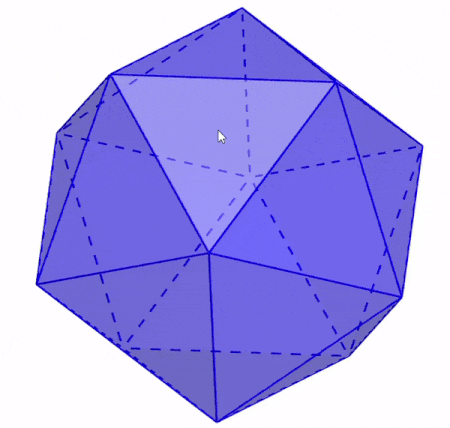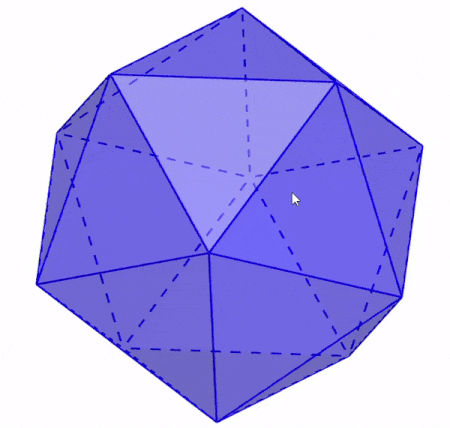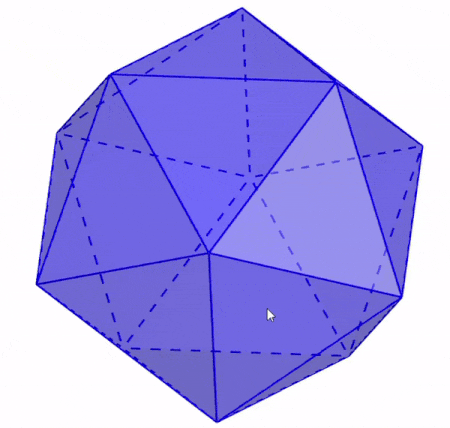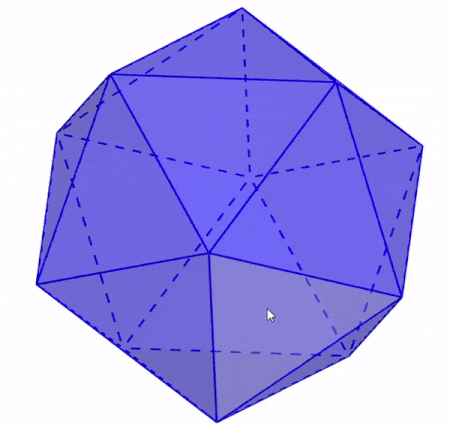
An important characteristic of the faces of an icosahedron is that they are congruent regular figures. That is, all twenty faces have the same shape and the same dimensions.
Therefore, we can calculate the surface area of an icosahedron by finding the area of one of the faces and multiplying it by 20. We can then form the following formula:
$latex A_{s}=20A_{t}$
where, $latex A_{t}$ is the area of one of the triangular faces of the icosahedron.
Alternatively, we can also use the standard formula for the Surface Area of an Icosahedron:
$latex A_{s}=5\sqrt{3}~{{a}^2}$
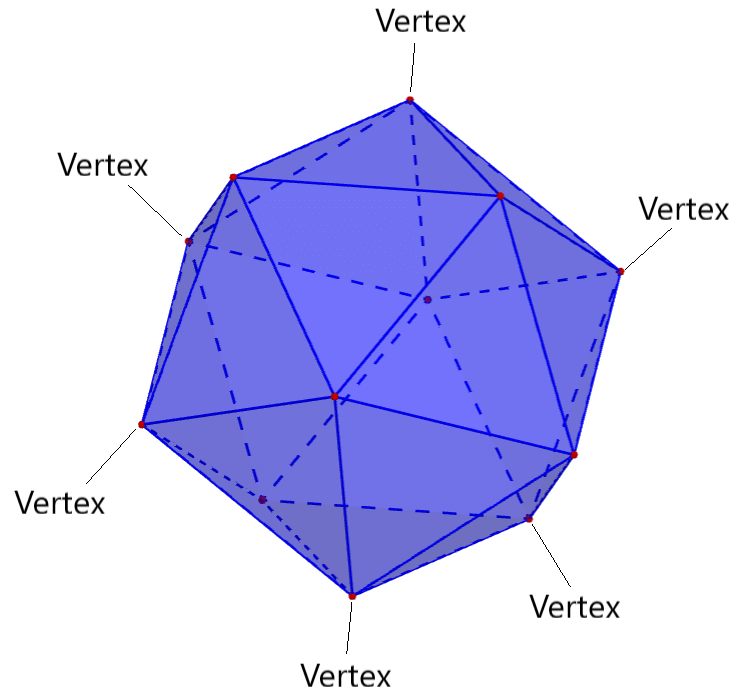
Vertices of an icosahedron
An icosahedron has a total of 12 vertices. The vertices are the points where the edges of the icosahedron meet. Specifically, five edges meet at each vertex of an icosahedron.
We can also consider the vertices of the icosahedrons to be the points where five triangular faces of the icosahedron meet.
Since each face of the icosahedron is triangular, each face is made up of 3 vertices.
Edges of an icosahedron
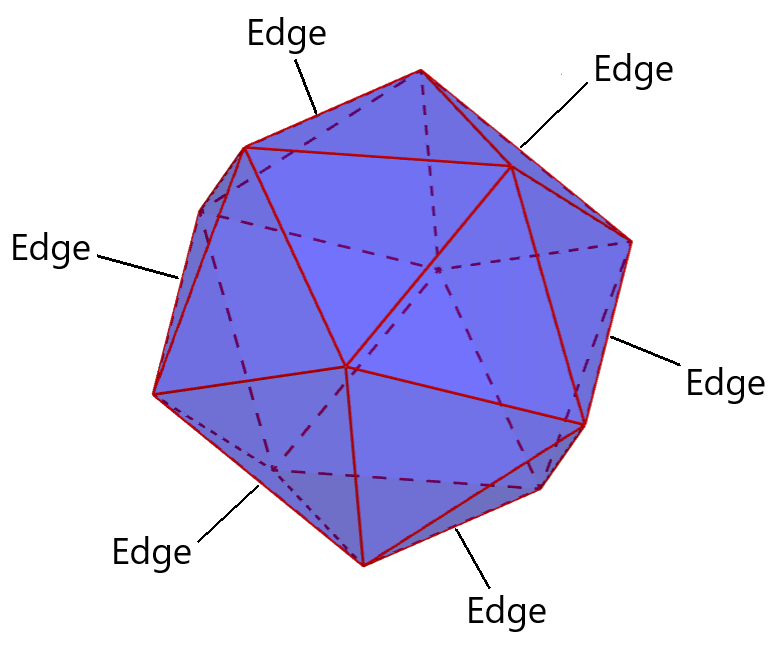
Icosahedrons have a total of 30 edges. Edges are the line segments that join two vertices. The edges, along with the vertices, form the outline of the triangular faces of the icosahedron.
We can also think of edges as the line segments where two triangular faces of the icosahedron meet. This means that the edges form the boundaries of the icosahedron.
Since all the faces of the icosahedron are triangular, each face has three edges. In the diagram below, we see that each face of the icosahedron has three edges, and each edge is shared by two faces.
See also
Interested in learning more about icosahedrons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
