The cross-sections of a sphere are two-dimensional figures formed by the intersection of a plane with a sphere. Since the sphere has a completely round shape with a constant radius, any plane that intersects a sphere will form a circular cross-section no matter the inclination of the plane.
Here, we will learn more about the cross-sections of a sphere. We will use diagrams and examples.
Circular cross-sections
A sphere is a perfectly round three-dimensional figure, which has a constant radius in all directions. This means that when we cut a sphere with a plane, we will always obtain a circular cross-section regardless of the inclination of the plane.
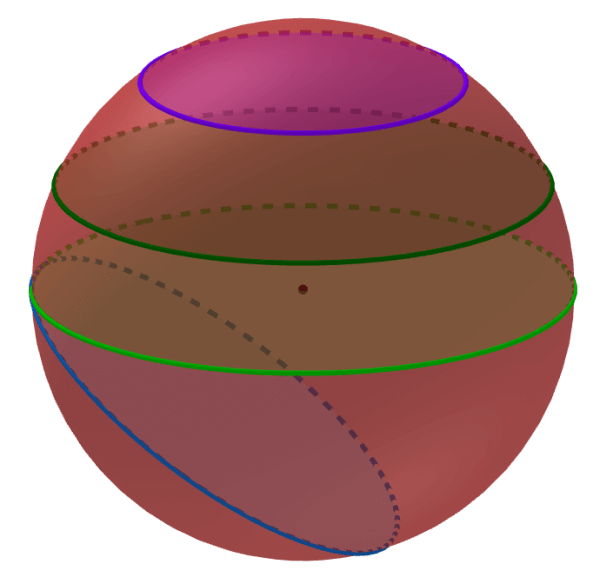
Depending on the orientation of the plane that cuts the sphere, we can have three types of cross-sections:
- Horizontal cross-section
- Vertical cross-section
- Inclined cross-section
However, as we have already mentioned, all cross-sections of a sphere will be circular.
Area of the cross-sections of a sphere
Since the cross-section is a two-dimensional figure, we can calculate its area if we have some information about the figure. For example, if we know the radius of the sphere and we know that the cross-section crosses through the center, we can use the formula for the area of a circle with the radius of the sphere.
Also, we can calculate the area of any cross-section of a sphere if we know its radius.
EXAMPLE 1
Find the cross-sectional area through the center of a sphere that has a radius of 5 m.
Solution: Since the cross-section passes through the center of the sphere, we know that the section will have the same diameter and radius as the sphere. Therefore, we can use the formula for the area of a circle with the given radius.
A=πr²
A=π(5)²
A=25π m²
EXAMPLE 2
What is the area of a cross-section of a sphere with a radius of 8 m?
Solution: Again, we just have to use the formula for the area of the circle with the given radius.
A=πr²
A=π(8)²
A=64π m²
See also
Interested in learning more about cross-sections of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
