Cylinder cross-sections are obtained when we cut a cylinder with a plane. Depending on the orientation of the plane, a cylinder can form three different cross-sections. If the plane is parallel to the bases, we get a circular cross-section. If the plane is perpendicular to the bases, we get a rectangular cross-section, and if the plane is at an angle to the bases, we get an oval cross-section.
Here, we will learn more about the cross-sections of a cylinder using diagrams.
Circular cross-section
We know that a cylinder is a 3D figure that has two circular bases connected by a curved surface. When a plane parallel to the bases intersects the cylinder, the cross-section obtained is a circle.
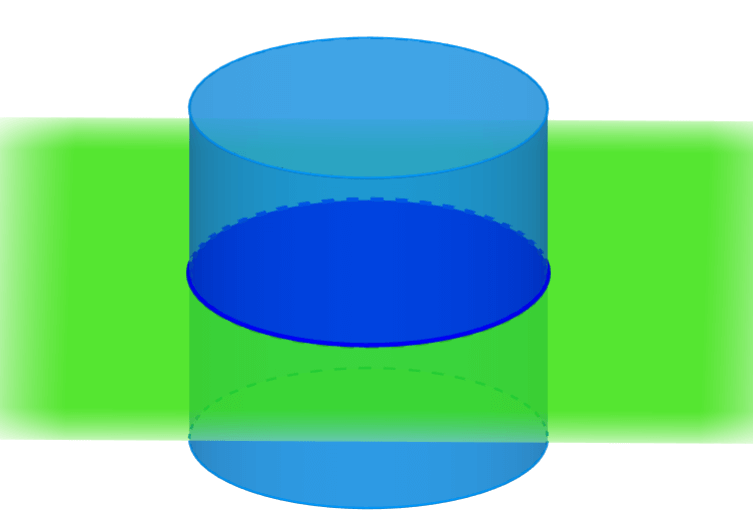
Area of the circular cross-section
If both circular bases of the cylinder are equal, the circular cross-sectional area is equal to the area of one of the circular bases. Therefore, we can find the area of this cross-section using the formula A=πr², where r is the radius of the cylinder.
EXAMPLE
If a cylinder has a radius of 5 m, what is the area of its circular cross-section?
Solution: The area of the circular cross-section is equal to the area of one of the bases. Therefore, we have:
A=πr²
A=π(5)²
A=25π m²
Rectangular cross-section
The rectangular cross-section is obtained when a plane cuts a cylinder in a direction perpendicular to the bases.
Area of the rectangular cross-section
Since the cross-section is a rectangle, we can calculate its area by multiplying the length of the base by the height. The base of the rectangle is equal to the diameter of the cylinder and the height is equal to the height of the cylinder. Therefore, we have:
A=dh
or alternatively:
A=2rh
EXAMPLE
Find the rectangular cross-sectional area of a cylinder that has a height of 8 m and a radius of 4 m.
Solution: Using the formula A=2rh, we have:
A=2rh
A=2(4)(8)
A=64 m²
Oval cross-section
We can get an oval cross-section when we cut a cylinder with a plane that is inclined at an angle greater than 0° and less than 90° to the base.
See also
Interested in learning more about cross-sections of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
