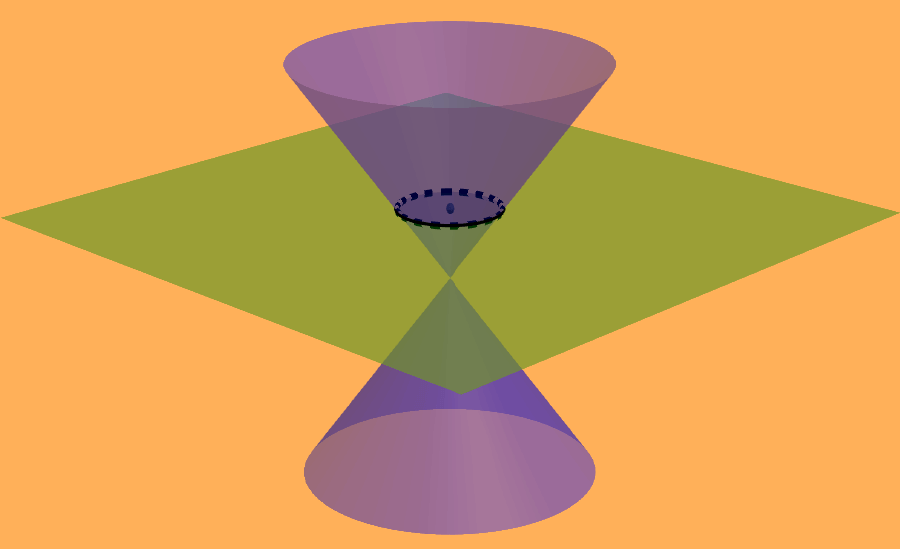
Cone cross-sections are obtained when we cut a cone with a plane. We can obtain different cross-sections depending on the orientation of the plane. It is possible to obtain circular, elliptical, parabolic, and hyperbolic cross-sections.
Here, we will learn about each of the cross-sections of a cone using diagrams.
Circular cross-section
When a cone is cut by a plane that is parallel to the bases, a circular cross-section is formed.
Circles have the following characteristics.
- Circles have a central point, called the center.
- The radius is the constant distance from the center to any point on the circle.
- The circles have an eccentricity of e=0.
Elliptical cross-section
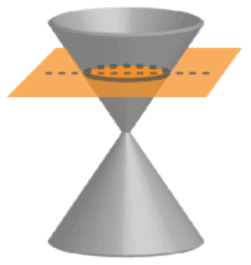
When a cone is cut by a plane that has an inclination with respect to the bases, an elliptical cross-section is formed. The angle of inclination of the plane must be less than the angle of the lateral sides.
Ellipses have the following characteristics:
- The longest diameter of the ellipse is called the major axis.
- The shortest diameter is called the minor axis.
- The center of the ellipse is the intersection of the two axes.
- The sum of the distances from any point on the ellipse to the two foci is constant.
Parabolic cross-section
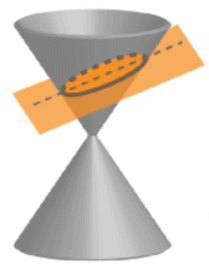
When a plane intersects a cone with an inclination parallel to the lateral sides of the cone, a parabolic cross-section is formed.
Parabolas have the following characteristics:
- The vertex is the lowest or highest point on the parabola. The vertex is the point where the curve changes direction.
- The focus is on the inside of the parabola.
- The directrix is on the outside of the parabola.
- The axis of symmetry is the line that connects the vertex and the focus and divides the parabola into two equal parts.
Hyperbolic cross-section
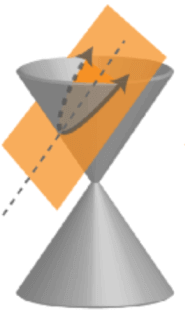
When a plane cuts a cone at a higher angle to the base of the cone, the cross-section formed is hyperbolic. The angle must be greater than the angle of the lateral sides.
Hyperbolas have the following characteristics:
- They are composed of two branches.
- The two vertices are located one on each branch. These points are located where each branch changes direction.
- The asymptotes are two straight lines that the curve approaches but never touches.
- The center is the intersection of the two asymptotes.
- The two foci are the fixed points, which define the shape of each branch.
See also
Interested in learning more about cross-sections of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
