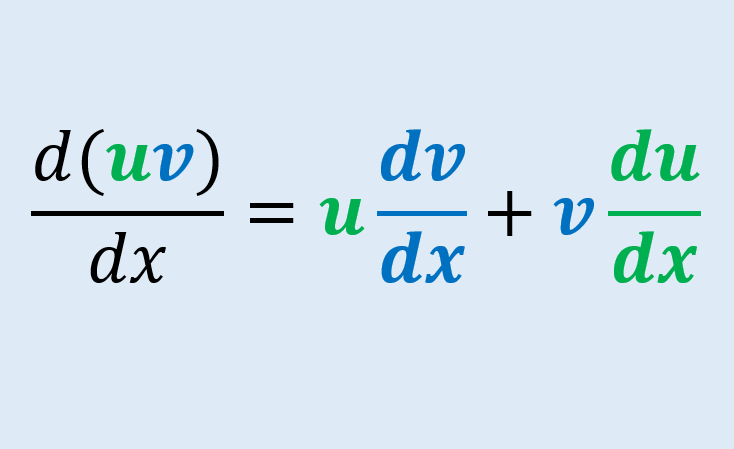Proofs of the Product Rule of Derivatives

What is the Product Rule?

The product rule is defined as the derivative of the product of at least two functions. The product rule can be used to derive any given product of functions such as but not limited to: 

$latex (fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$

where f(x) and g(x) can be equivalent to any types of functions.

But how exactly do we derive that given function using the product rule?

The product rule states that the derivative of a product of two functions is equal to the first function f(x) in its original form multiplied by the derivative of the second function g(x) and then added to the original form of the second function g(x) multiplied by the derivative of the first function f(x).

To better illustrate, when you are given two functions f(x) and g(x) and then you are asked to get the derivative of fg(x) or the derivative of the product of f(x) and g(x), we have: 

$$(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$$

Easy, right? But we should not take this formula superficially if we aim to be able to derive any product of functions. In order to learn and understand the concepts behind the development of this product rule formula, we need to be familiarized with any proof which would satisfy the statement of the product rule.

---

Proof of The Product Rule Using Limits

In this article, you are highly recommended to be familiarized with the topics, The Slope of a Tangent Line and Derivatives Using Limits, as a pre-requisite to better understand The Proof of The Product Rule Using Limits.

We can recall that

$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$

By applying limits, we can derive a function f(x). But how about a product of two functions f(x) and g(x)?

For instance, we are given two functions f(x) and g(x) and then, we are asked to get the derivative of fg(x); we have 

$$(fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$$

To derive the product of these two functions using limits, we have the following:

Let

$$\Upsilon(x) = f(x) \cdot g(x)$$

Then we have,

$$\Upsilon'(x) = \frac{d}{dx}(f(x) \cdot g(x))$$

and we can derive it by

$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\Upsilon(x+h)-\Upsilon(x)}{h}}$$

By substituting the equation $latex \Upsilon(x) = f(x) \cdot g(x)$, we have

$$ \Upsilon'(x) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x) \cdot g(x)}{h}}$$

which can be clearly re-written as:

$$\frac{d}{dx}(f(x) \cdot g(x)) =\lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x) \cdot g(x)}{h}}$$

This represents the derivative of a product in terms of limits. Now, this equation cannot be algebraically manipulated easily to arrive at the product rule formula that we are trying to prove.

However, we can add and subtract $latex f(x+h) \cdot g(x)$ to the numerator. Hence, we have

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x+h) \cdot g(x) + f(x+h) \cdot g(x) – f(x) \cdot g(x)}{h}}$$

Given that $$+ f(x+h) \cdot g(x) – f(x+h) \cdot g(x) = 0$$, we didn’t change the equation at all.

Now, we can factor $latex f(x+h)$ from the first two terms and $latex g(x)$ from the last two terms. Then, we can split it into two parts and by simplifying, we have,

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot (g(x+h)-g(x))}{h} +\lim \limits_{h \to 0} \frac{g(x) \cdot (f(x+h)-f(x))}{h}}$$

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h) \cdot \frac{g(x+h)-g(x)}{h} +\lim \limits_{h \to 0} g(x) \cdot \frac{f(x+h)-f(x)}{h}}$$

By applying the properties of limits to solve the equation, we have

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h)} \cdot \lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}} + \lim \limits_{h \to 0} {g(x)} \cdot \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$

The limits $latex \lim \limits_{h \to 0} {f(x+h)}$ and $latex \lim \limits_{h \to 0} {g(x)}$ can be easily solved. When h tends to zero, we will simply get $latex f(x)$ and $latex g(x)$ respectively.

The limits $latex \lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}}$ and $latex \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$ look more complicated, but they are simply the derivatives of $latex g(x)$ and $latex h(x)$ expressed in limits. Therefore, we have:

$$\frac{d}{dx}(f(x) \cdot g(x)) = f(x) \cdot \frac{d}{dx}(g(x)) + g(x) \cdot \frac{d}{dx}(f(x))$$

or it can be simply illustrated as

$$(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$$

which is now The Product Rule Formula.

---

Proof of The Product Rule Using The Chain Rule

Another way that might make the product rule easier to prove and formulate is by applying the chain rule formula. Hence, you are highly recommended to be familiarized with the topics, The Chain Rule Formula, The Sum/Difference of Derivatives, as a prerequisite to better understand this proof.

We can recall that the chain rule formula is

$$ \frac{d}{dx}[(f(x))^n] = n \cdot (f(x))^{n-1} \cdot \frac{d}{dx}(f(x))$$

To make the derivation of the product rule easier, we can consider the following expression:

$$\Upsilon(x) = {{(f+g)}^2}$$

where, f and g are two valid functions.

We are going to derive $latex \Upsilon(x)$ by applying the chain rule. Therefore, we have:

$latex \Upsilon'(x)= 2(f+g)(f’+g’)$

If we multiply and expand the parentheses, we have:

$latex \Upsilon'(x)= 2(ff’+fg’+gf’+gg’)$

$latex = 2ff’+2fg’+2gf’+2gg’$

Now, instead of using the chain rule, we can expand the expression $latex {{(f+g)}^2}$ to get:

$latex \Upsilon(x) = {{f}^2}+fg+{{g}^2}$

If we differentiate term by term, we get:

$latex \Upsilon'(x)= 2ff’+2(fg)’+2gg’)$

Since the two expressions we got for $latex \Upsilon'(x)$ are equivalent, we have:

$$2ff’+2(fg)’+2gg’)= 2ff’+2fg’+2gf’+2gg’$$

$latex (fg)’= fg’+gf’$

We have clearly arrived at the product rule.

---

Proof of the Product Rule using logarithmic differentiation

A third method we can use to prove the product rule is by using logarithmic differentiation and implicit differentiation. This is a quicker method but requires you to be familiarized with both topics.

We can start by writing the following expression:

$latex y=f(x)g(x)$

Now, we can take the natural logarithm of both sides:

$latex \ln(y)=\ln(f(x)g(x))$

By using the laws of logarithms on the right side, we can write:

$latex \ln(y)=\ln f(x)+\ln g(x)$

Taking the derivative of both sides, we have:

$$\frac{y’}{y}=\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}$$

Solving for $latex y’$, we have:

$$y’=y\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$$

Now, we can substitute $latex y=f(x)g(x)$ to get:

$$(fg)’=f(x)g(x)\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$$

If we multiply and expand the parentheses, we get:

$latex (fg)’=g(x)f'(x)+f(x)g'(x)$

We have arrived at the product rule.

---

See also

Interested in learning more about the product rule? Take a look at these pages:

• Product Rule – Formula, Proof and Examples
• Product Rule – Examples and Practice Problems