To differentiate a sum or difference of functions, we have to differentiate each term of the function separately. This means that we can simply apply the power rule or another relevant rule to differentiate each term in order to find the derivative of the entire function.
Here, we will solve 10 examples of derivatives of sum and difference of functions. In addition, we will explore 5 problems to practice the application of the sum and difference rule.
CALCULUS
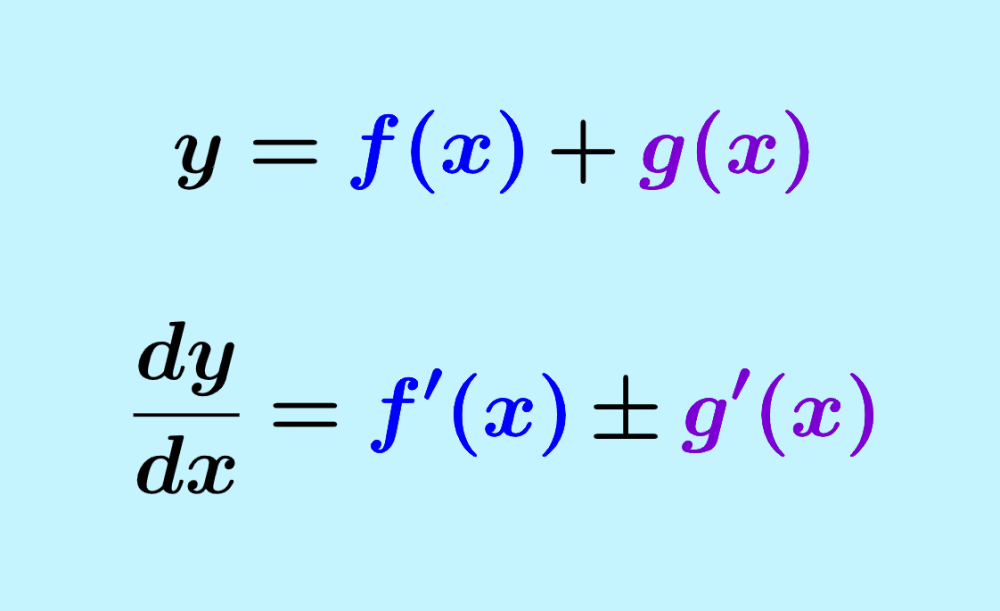
Relevant for…
Solving examples of derivatives of sum and difference of functions.
CALCULUS
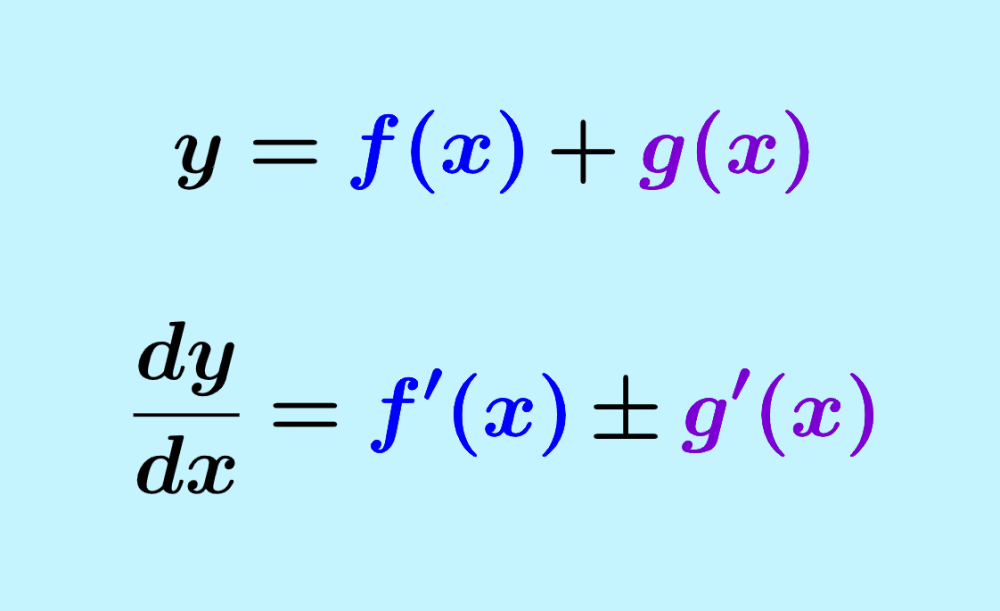
Relevant for…
Solving examples of derivatives of sum and difference of functions.
Statement and formula for the sum and difference rule of derivatives
The sum and difference rule of derivatives states that the derivative of a sum or difference of functions is equal to the sum of the derivatives of each of the functions.
This means that when $latex y$ is made up of a sum or a difference of more than one function, we can find its derivative by differentiating each function individually.
The sum and difference rule of derivatives allows us to find the derivative of functions like the following:
$latex y=f(x)+g(x)$
In this case, its derivative is equal to:
$$\frac{dy}{dx}=f'(x) \pm g'(x)$$
This applies to the sum or difference of any number of functions.
To derive each of the functions or each of the terms, we use the power rule, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, or any other applicable derivative rule.
How differentiate a sum or difference of two or more functions
Suppose we have to derive
$latex f(x) = x^2+5x$
We have a function that is a sum of two terms. Then, we can derive it by following these steps:
1. Use the laws of exponents to transform radicals or rational expressions into exponential form.
In this case, we have no radicals or rational expressions. Note: An example would be to write $latex \sqrt{x}$ as $latex x^{\frac{1}{2}}$.
2. Apply the power rule formula, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, or other applicable rules to each term in the sum or difference:
$$f'(x) = 2x+5$$
3. Simplify the resulting expression.
In this case, we can no longer simplify. Note: An example would be to write $latex x^{-\frac{1}{2}}$ as $latex \frac{1}{\sqrt{x}}$.
You can use $latex f'(x), y’,$ or $latex \frac{d}{dx}(f(x))$ as the derivative symbol on the left-hand side of the final answer.
10 Examples of derivatives of sum and difference of functions
EXAMPLE 1
Find the derivative of $latex f(x)=x^4+5x$.
Solution
Step 1: We start by converting radical or rational expressions to their exponential form. In this case, we don’t have radicals or variables written in rational form.
Step 2: We use the power rule formula, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, to differentiate both terms of the function:
$latex f(x)=x^4+5x$
$latex f'(x)=4(x^{4-1})+5(x^{1-1})$
$latex f'(x)=4x^3+5$
Step 3: We simplify if possible. In this case, the expression is simplified.
EXAMPLE 2
What is the derivative of the function $latex f(x)=-5x^3+10x^2$?
Solution
Step 1: The function has no radicals or rational expressions.
Step 2: Let’s differentiate using the power rule, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, to differentiate both terms of the function:
$latex f(x)=-5x^3+10x^2$
$latex f(x)=3(-5x^{3-1})+2(10x^{2-1})$
$latex f'(x)=-15x^2+20x$
Step 3: The function is now simplified.
EXAMPLE 3
Find the derivative of the function $latex f(x)=7x^8+5x^{-3}$.
Solution
Step 1: Both terms have variables with numerical exponents.
Step 2: We have a negative exponent, but we simply use the power rule to differentiate both terms:
$latex f(x)=7x^8+5x^{-3}$
$latex f(x)=8(7x^{8-1})+(-3)(5x^{-3-1})$
$latex f'(x)=56x^7-15x^{-4}$
Step 3: Using the laws of exponents, we can write as follows:
$$f'(x)=56x^7-\frac{15}{x^4}$$
EXAMPLE 4
Find the derivative of the function $latex f(x)=3x^{-5}-2x^{-2}$.
Solution
Step 1: We have negative exponents, but there are no radicals or variables with rational expressions.
Step 2: We use the power rule formula, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, to differentiate both terms of the function:
$latex f(x)=3x^{-5}-2x^{-2}$
$latex f(x)=-5(3x^{-5-1})-2(-2x^{-2-1})$
$latex f'(x)=-15x^{-6}+4x^{-3}$
Step 3: We use the laws of exponents to simplify:
$$f'(x)=-\frac{15}{x^6}+\frac{4}{x^3}$$
EXAMPLE 5
What is the derivative of the function $latex f(x)=-5x^4+ \frac{1}{x}$?
Solution
Step 1: Using the laws of exponents, we can write as follows:
$latex f(x)=-5x^4+ x^{-1}$
Step 2: Now that we only have numerical exponents, we use the power rule formula, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, on both terms of the function:
$latex f(x)=-5x^4+ x^{-1}$
$latex f'(x)=-20x^3-x^{-2}$
Step 3: With the laws of exponents, we can write as follows:
$$f'(x)=-20x^3-\frac{1}{x^2}$$
EXAMPLE 6
What is the derivative of $latex f(x)=4x^3+2x^2+\frac{2}{x^3}$?
Solution
Step 1: We start by converting the rational expression to an expression with a numerical exponent:
$latex f(x)=4x^3+2x^2+2x^{-3}$
Step 2: Using the power rule for the three terms, we have:
$latex f(x)=4x^3+2x^2+2x^{-3}$
$latex f'(x)=12x^2+4x-6x^{-4}$
Step 3: We use the laws of exponents again to write as follows:
$$f'(x)=12x^2+4x-\frac{6}{x^4}$$
EXAMPLE 7
Determine the derivative of $latex f(x)=3x^2+\frac{2}{3x^2}+ x^{ \frac{1}{2}}$.
Solution
Step 1: We use the laws of exponents to write the function like this:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
Step 2: Using the power rule on the three terms of the function, we have:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
$$f'(x)=6x-\frac{4}{3}x^{-3}-\frac{1}{2}x^{-\frac{3}{2}}$$
Step 3: We simplify by writing as follows:
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2\sqrt{x^3}}$$
EXAMPLE 8
Find the derivative of the function $latex f(x)=\sqrt{x}+ \frac{3}{x^3} $.
Solution
Step 1: Applying the laws of exponents, we can write as follows:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
Step 2: We apply the power rule to derive both terms:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
$$f'(x)=\frac{1}{2}x^{-\frac{1}{2}}-9x^{-4}$$
Step 3: Using the laws of exponents again, we can write as follows:
$$f'(x)=\frac{1}{2x^{\frac{1}{2}}}-\frac{9}{x^4}$$
$$f'(x)=\frac{1}{2\sqrt{x}}-\frac{9}{x^4}$$
EXAMPLE 9
Find the derivative of $latex f(x)=5x^{-5}+\frac{1}{\sqrt{x}}$.
Solution
Step 1: We start by writing as follows:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
Step 2: Differentiating both terms with the power rule, we have:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
$$f'(x)=-25x^{-6}-\frac{1}{2}x^{-\frac{3}{2}}$$
Step 3: We simplify the resulting expression using the laws of exponents:
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2\sqrt{x^3}}$$
EXAMPLE 10
Determine the derivative of $latex f(x)=\frac{2}{3x^2}+ \frac{1}{\sqrt[3]{x^2}}- \frac{5}{x}$.
Solution
Step 1: We start by using the laws of exponents to write like this:
$$f(x)=\frac{2}{3}x^{-2}+ x^{\frac{2}{3}}- 5x^{-1}$$
Step 2: We use the power rule to derive the terms:
$$f(x)=\frac{2}{3}x^{-2}+ x^{-\frac{2}{3}}- 5x^{-1}$$
$$f'(x)=-\frac{4}{3}x^{-3}- \frac{2}{3}x^{-\frac{5}{3}}+ 5x^{-2}$$
Step 3: Finally, we simplify as follows:
$$f'(x)=-\frac{4}{3x^3}- \frac{2}{3x^{\frac{5}{3}}}+ \frac{5}{x^2}$$
$$f'(x)=-\frac{4}{3x^3}- \frac{2}{3\sqrt[3]{x^5}}+ \frac{5}{x^2}$$
Sum and difference rule of derivatives – Practice problems


Find the value of $latex f'(5)$ if we have the following function: $$f(x)=4x^3-6x^2+3x-10$$
Write the answer in the input box.
See also
Interested in learning more about derivatives? You can take a look at these pages:



