The equation of the tangent line to a curve is found using the form y=mx+b, where m is the slope of the line and b is the y-intercept. In turn, we find the slope of the tangent line by using the derivative of the function and evaluating it at the given point.
Here, we will look at 10 examples in which we will find the equation of the tangent line to a curve. Additionally, we will explore 5 practice problems.
How to find the equation for the tangent line to a curve
The equation of the tangent line to a curve can be found using the form $latex y=mx+b$, where m is the slope of the line and b is the y-intercept.
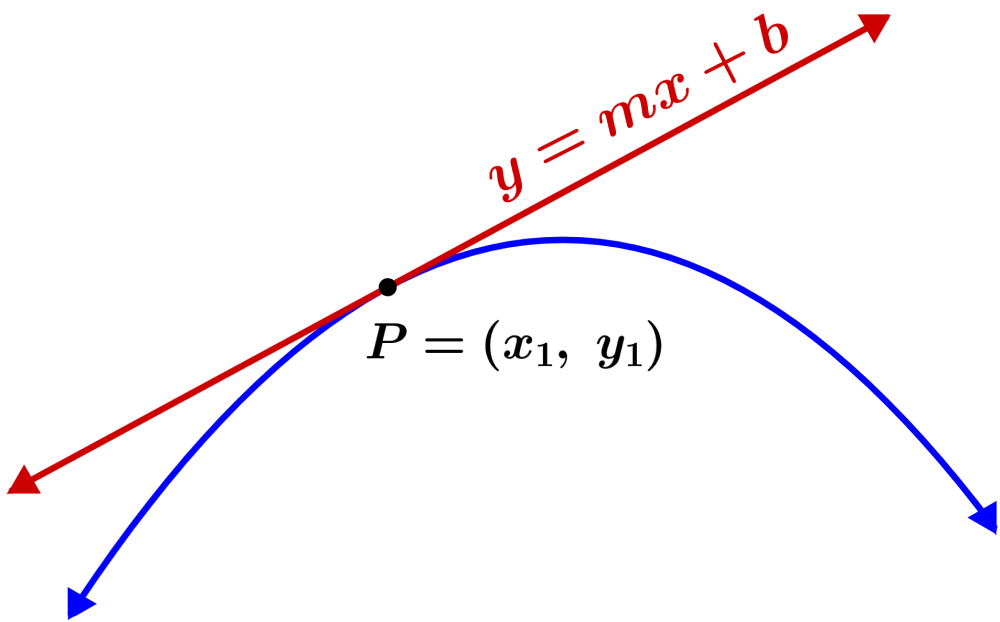
Therefore, if we want to find the equation of the tangent line to a curve at the point $latex (x_{1},~y_{1})$, we can follow these steps:
1. Find the derivative of the function that represents the curve.
2. Use the derivative of the function to find the slope of the tangent line at the point $latex (x_{1},~y_{1})$.
For this, we use the x-coordinate of the point in the derivative of the function. That is, we have $latex m=f'(x_{1})$.
3. Use the equation $latex y=mx+b$ to find the value of b.
Use the value of the slope found in step 2 and substitute the x and y coordinates of the given point to find the value of b. That is, we have $latex y_{1}=mx_{1}=b$.
4. Substitute the values of m and b into the equation $latex y=mx+b$.
Look at the following examples to learn how to apply these steps to find the equation of the tangent line to a function.
10 Examples of the tangent line to a curve with answers
EXAMPLE 1
What is the equation of the tangent line to the curve $latex f(x)=x^2$ at the point P=(1, 3)?
Solution
To find the equation of the tangent line, we can use the form $latex y=mx+b$, where m is the slope and b is the y-intercept.
The slope of the tangent line is found by evaluating the derivative of the function at the given point. That is, the slope is equal to $latex f'(1)$. Therefore, we have:
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex m=f'(1)=2(1)$
$latex m=2$
So far, we have the equation $latex y=2x+b$. Now, we can find the value of b using the point (1, 3) in the equation:
$latex y=2x+b$
$latex 3=2(1)+b$
$latex b=1$
The equation of the tangent line at the point (1, 3) is $latex y=2x+1$.
EXAMPLE 2
Find the equation of the tangent line to the function $latex f(x)=x^3-10x$ at the point (2, 1).
Solution
We need the derivative of the function to find the slope of the tangent line. Thus, we have:
$latex f(x)=x^3-10x$
$latex f'(x)=3x^2-10$
To find the slope of the tangent line at the point (2, 1), we evaluate $latex f'(2)$:
$latex m=f'(2)=3(2)^2-10$
$latex m=2$
We form the equation $latex y=2x+b$. Now, we find the value of b, using the point (2, 1) in the equation:
$latex y=2x+b$
$latex 1=2(1)+b$
$latex b=-1$
The equation of the tangent line at the point (2, 1) is $latex y=2x-1$.
EXAMPLE 3
If we have the function $latex f(x)=2x^3-7x^2$, find the tangent at the point (2, 3).
Solution
The derivative of the function allows us to find the slope of the tangent line. The derivative of the given function is:
$latex f(x)=2x^3-7x^2$
$latex f'(x)=6x^2-14x$
The slope of the tangent line at the point (2, 3) is equal to $latex f'(2)$. Thus, we have:
$latex m=f'(2)=6(2)^2-14(2)$
$latex m=24-28$
$latex m=-4$
Using the slope found, we have the equation $latex y=-4x+b$. Now, we find the value of b, using the point (2, 3) in the equation:
$latex y=-4x+b$
$latex 3=-4(2)+b$
$latex b=11$
The equation of the tangent line at the point (2, 3) is $latex y=-4x+11$.
EXAMPLE 4
We have the function $latex f(x)=x^3+\frac{8}{x}$. What is the tangent line at the point (2, 4)?
Solution
We start by finding the derivative of the function:
$latex f(x)=x^3+8x^{-1}$
$latex f'(x)=3x^2-8x^{-2}$
$latex f'(x)=3x^2-\frac{8}{x^2}$
The slope of the tangent at the point (2, 4) is found by evaluating $latex f'(2)$. Therefore, we have:
$latex m=f'(2)=3(2)^2-\frac{8}{2^2}$
$latex =12-2$
$latex m=10$
We have the equation $latex y=10x+b$. Now, we use the point (2, 4) to find the value of b:
$latex y=10x+b$
$latex 4=10(2)+b$
$latex b=-15$
The equation of the tangent line at the point (2, 4) is $latex y=10x-15$.
EXAMPLE 5
What is the tangent line to $latex f(x) = -x^{-2}+\sqrt{x}$ at the point (1, 3)?
Solution
We start by finding the derivative of the function to determine the slope of the tangent line:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
The slope of the tangent at the point (1, 3) is equal to $latex f'(1)$, so we have:
$$m=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m=\frac{5}{2}$
Now that we have formed the equation $latex y=\frac{5}{2}x+b$, we use the point (1, 3) to find the value of b:
$$y=\frac{5}{2}x+b$$
$$3=\frac{5}{2}(1)+b$$
$latex b=\frac{1}{2}$
The equation of the tangent line at the point (1, 3) is $latex y=\frac{5}{2}x+\frac{1}{2}$.
EXAMPLE 6
If we have the function $latex f(x)=\sin(x)-\cos(x)$, what is the equation of the tangent line at the point (0, 1)?
Solution
We start by finding the derivative of the function:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
Now, we know that the slope of the tangent line at the point (0, 1) is found by evaluating $latex f'(0)$. Thus, we have:
$latex m=f'(0)=\cos(0)+\sin(0)$
$latex m=1+0$
$latex m=1$
So far, we have the equation $latex y=x+b$ and we can use this equation with the point (0, 1) to find the value of b, using the point (0, 1) in the equation:
$latex y=x+b$
$latex 1=0+b$
$latex b=1$
The equation of the tangent line at the point (0, 1) is $latex y=x+1$.
EXAMPLE 7
Find the tangent line to $latex f(x)=-2\sin(2x)+\cos(3x)$ at the point (0, 1).
Solution
We need the derivative of the function to find the slope of the tangent. Thus, we have:
$latex f(x)=-2\sin(2x)+\cos(3x)$
$latex f'(x)=-4\cos(2x)-3\sin(3x)$
Now, we can evaluate $latex f'(0)$ to determine the slope of the tangent line at the point (0, 1):
$latex m=f'(0)=-4\cos(2(0))-3\sin(3(0))$
$latex m=-4+0$
$latex m=-4$
Using the slope found, we have the equation $latex y=-4x+b$. Using this equation with the point (0, 1) we find the value of b:
$latex y=-4x+b$
$latex 1=0+b$
$latex b=1$
The equation of the tangent line at the point (0, 1) is $latex y=-4x+1$.
EXAMPLE 8
What is the tangent line to $latex f(x)=x^2-3x+1$ at the point where the curve intersects the y-axis?
Solution
The derivative of the function is:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
The statement tells us that we have to find the tangent line at the point where the curve intersects the y-axis. This happens when the coordinates in x are equal to 0. Then, we have:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Therefore, the point of the tangent is (0, 1). Now, we evaluate $latex f'(0)$ to find the slope of the tangent, and we have:
$latex m=f'(0)=2(0)-3$
$latex m=-3$
The slope found gives us the equation $latex y=-3x+b$. To find the value of b, we use the point (0, 1) in the equation:
$latex y=-3x+b$
$latex 1=-3(0)+b$
$latex b=1$
The equation of the tangent line at the point (0, 1) is $latex y=-3x+1$.
EXAMPLE 9
Find the equations of the two tangent lines to $latex f(x)=x^2-5x+4$ at the points where the function intersects the x-axis.
Solution
The points where the function intersects the x-axis are the zeros of the function. Therefore, we start by finding the zeros:
$latex x^2-5x+4=0$
$latex (x-4)(x-1)=0$
The function cuts the x-axis when $latex x=4$ and $latex x=1$. Also, the y-values at those points are 0, so we have (4, 0) and (1, 0).
Now, we find the derivative and evaluate $latex f'(4)$ and $latex f'(1)$ to determine the slopes of the tangent lines.
$latex f(x)=x^2-5x+4$
$latex f'(x)=2x-5$
$latex f'(4)=2(4)-5=3$
$latex f'(1)=2(1)-5=-3$
Now, we find the values of b using the form $latex y=mx+b$ with the slopes found and the coordinates of each point.
$latex 0=3(4)+b_{1}$
$latex b_{1}=-12$
$latex 0=-3(1)+b_{2}$
$latex b_{2}=3$
Therefore, the equations of the tangent lines are $latex y=3x-12$ and $latex y=-3x+3$.
EXAMPLE 10
Find the two tangent lines to the function $latex f(x)=x^2$ at the points where $latex y=9$.
Solution
The statement tells us that the lines are tangent at the points where $latex y=9$. Therefore, we have to find the values of x when $latex y=9$:
$latex x^2=9$
$latex x=\pm \sqrt{9}$
$latex x=3~~$ or $latex ~~x=-3$
Now, we use the derivative of the function to find the slopes of the lines by evaluating $latex f'(3)$ and $latex f'(-3)$.
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex f'(3)=2(3)=6$
$latex f'(-3)=2(-3)=-6$
Using the form $latex y=mx+b$ with the slopes found and the coordinates of each point (the y-values are 9 in both cases), we can find the values of b:
$latex 9=6(3)+b_{1}$
$latex b_{1}=-9$
$latex 9=-6(-3)+b_{2}$
$latex b_{2}=-9$
Therefore, the equations of the tangent lines are $latex y=6x-9$ and $latex y=-6x-9$.
Tangent to a curve – Practice problems


We have the function $latex f(x)=\frac{9}{x}$. Find the tangent line when $latex x=-3$.
Write the equation in the input box.
See also
Interested in learning more about equations of tangent and normal lines to functions? You can take a look at these pages:



