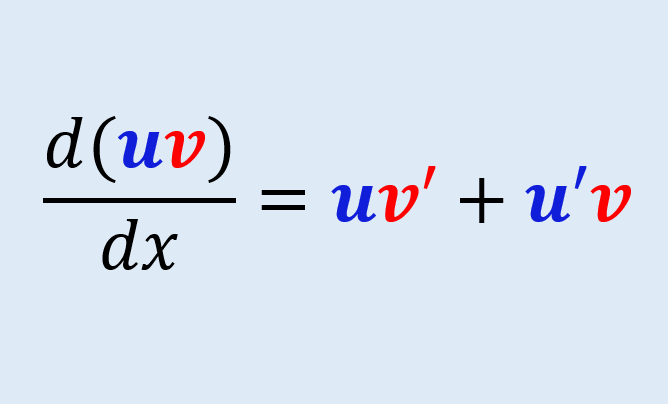The Product Rule is one of the main principles applied in Differential Calculus (or Calculus I). It is commonly used in deriving a function that involves the multiplication operation. The product rule was proven and developed using the backbone of Calculus, which is the limits.
In this article, we will discuss everything about the product rule. We will cover its definition, formula, and application usage. We will also look at some examples and practice problems to apply the principles of the product rule.
- The product rule and its formula
- How to use the product rule, a step-by-step tutorial
- Product Rule – Examples with answers
- Product Rule – Practice Problems
- See also
- The Product Rule and its Formula
- Proofs of the Product Rule
- When to use the Product Rule to find derivatives
- How to use the Product Rule, a step by step tutorial
- Product Rule – Examples with answers
- Product Rule – Practice problems
- See also
The product rule and its formula
What is the product rule?
The product rule is a rule that states that a product of at least two functions can be derived by obtaining the sum of (a) the first function in its original form multiplied by the derivative of the second function and (b) the second function in its original form multiplied by the derivative of the first function.
The formula for product rule of derivatives
The formula for the product rule is:
$$(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$$
where
$latex u =$ first function $latex f(x)$ or the first multiplicand
$latex v =$ second function $latex g(x)$ or the second multiplicand
Or in other forms, it may be:
$$\frac{d}{dx}(F(x)) = f(x) \cdot \frac{d}{dx}(g'(x)) + g(x) \cdot \frac{d}{dx}(f(x))$$
or
$$\frac{d}{dx}(uv) = uv’ + vu’$$
which is the most commonly used form of the product rule formula where
$latex u = f(x)$
$latex v = g(x)$
and $latex \frac{d}{dx}(uv)$ can also be $latex y’$, $latex F'(x)$, $latex{\Upsilon}’$ or other letters used to denote functions with the apostrophe symbol.
Check out our article on the proofs of the product rule to learn how to prove the product rule step by step.
The product rule for three or more functions
See this article for the rule of the product of three or more functions.
How to use the product rule, a step-by-step tutorial
Suppose we have to derive
$latex f(x) = x^2 \sin{(x)}$
As you can see, this given function has two multipliers, but they can’t be multiplied algebraically or simplified. Then, we can use the product rule as shown in the following steps:
1. Identify the multipliers of the given function.
In this case, we have $latex u = x^2$ and $latex v = \sin{(x)}$.
2. Find the derivatives of $latex u$ and $latex v$.
In this case, we have $latex u’ = 2x$ and $latex v’ = \cos{(x)}$.
3. Apply the product rule formula.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (x^2) \cdot (\cos{(x)}) + (\sin{(x)}) \cdot (2x)$$
4. Simplify the derivative.
$latex \frac{d}{dx}(uv) = x^2 \cos{(x)} + 2x \sin{(x)}$
$latex f'(x) = x^2 \cos{(x)} + 2x \sin{(x)}$
For formality purposes, it is recommended to use $latex f'(x), y’,$ or $latex \frac{d}{dx}(f(x))$ as your derivative symbol on the left-hand side of the answer final instead of $latex (uv)’$ or $latex \frac{d}{dx}(uv)$.
Product Rule – Examples with answers
EXAMPLE 1
Derive the following function:
$latex f(x) = x^3 (x-5)$
Solution
Step 1: In the chosen form of the product rule formula, we will mark the first multiplicand as $latex u$ and the second multiplicand as $latex v$.
Therefore, we have
$latex u = x^3$
$latex v = (x-5)$
Step 2: Differentiate $latex u$ y $latex v$ individually:
$latex u’ = 3x$
$latex v’ = (1-0)$
Step 3: Apply the formula for the product rule now by substituting $latex u$, $latex u’$, $latex v$, and $latex v’$:
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (x^3) \cdot (1-0) + (x-5) \cdot (3x)$$
Step 4: Simplify algebraically:
$latex \frac{d}{dx}(uv) = x^3 + 3x (x-5)$
$latex \frac{d}{dx}(uv) = x^3 + 3x^2 – 15x$
$latex f'(x) = x^3 + 3x^2 – 15x$
EXAMPLE 2
Find the derivative of the following function:
$latex f(x) = \sin{(x)} \tan{(x)}$
Solution
Step 1: In the chosen form of the product rule formula, we will mark the first multiplicand as $latex u$ and the second multiplicand as $latex v$.
Therefore, we have
$latex u = \sin{(x)}$
$latex v = \tan{(x)}$
Step 2: Find the derivatives of $latex u$ and $latex v$:
$latex u’ = \cos{(x)}$
$latex v’ = \sec^{2}{(x)}$
Step 3: Apply the formula for the product rule substituting $latex u$, $latex u’$, $latex v$ and $latex v’$.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (\sin{(x)}) \cdot (\sec^{2}{(x)})+ (\tan{(x)}) \cdot (\cos{(x)})$$
Step 4: Simplify algebraically and since we have a trigonometric function in our derivative, we can also apply some applicable trigonometric identities in our solution:
$$\frac{d}{dx}(uv) = \sin{(x)} \sec^{2}{(x)} + \tan{(x)} \cos{(x)}$$
$$\frac{d}{dx}(uv) = (\sin{(x)}) (\frac{1}{\cos{(x)}})^2+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = (\sin{(x)}) (\frac{1^{2}}{\cos^{2}{(x)}})+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = (\frac{\sin{(x)}}{\cos{(x)}}) (\frac{1}{\cos{(x)}})+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = \sec{(x)} \tan{(x)} + \sin{(x)}$$
$latex f'(x) = \sec{(x)} \tan{(x)} + \sin{(x)}$
EXAMPLE 3
Derive the following function:
$latex x^{2} \sin^{2}{(x)}$
Solution
Step 1: We have the first multiplicand as $latex u$ and the second multiplicand as $latex v$.
Therefore, we have
$latex u = x^{2}$
$latex v = \sin^{2}{(x)}$
Step 2: Differentiate $latex u$ and $latex v$:
$latex u’ = 2x$
$latex v’ = 2 \sin{(x)} \cos{(x)}$
Step 3: Apply the formula for the product rule substituting $latex u$, $latex u’$, $latex v$ and $latex v’$:
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = x^{2} \cdot (2 \sin{(x)} \cos{(x)})+ (\sin^{2}{(x)}) \cdot (2x)$$
Step 4: Simplify algebraically and since we have a trigonometric function in our derivative, we can also apply some applicable trigonometric identities in our solution:
$$\frac{d}{dx}(uv) = x^{2} \cdot (2 \sin{(x)} \cos{(x)})+ (\sin^{2}{(x)}) \cdot (2x)$$
$$\frac{d}{dx}(uv) = 2x^{2} \sin{(x)} \cos{(x)} + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} (2 \sin{(x)} \cos{(x)}) + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} \sin{(2x)} + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} \sin{(2x)} + 2x \sin^{2}{(x)}$$
EXAMPLE 4
What is the derivative of $latex f(x) = 5x^7 \cot{(x^7)}$?
Solution
In this problem, we have two multipliers in the function f(x). The first multiplicand is $latex u=5x^7$ and the other is $latex v=\cot{(x^7)}$.
Therefore, we have
$latex u = 5x^7$
$latex v = \cot{(x^7)}$
$latex f(x) = uv$
Now, we can use the product rule formula:
$latex f'(x) = uv’ + vu’$
$$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$$
$$\frac{d}{dx}f(x) = 5x^7 \cdot \frac{d}{dx}(\cot{(x^7)}) + \cot{(x^7)} \cdot \frac{d}{dx}(5x^7)$$
Note: The derivative of $latex u$ uses the power rule formula and the derivative of $latex v$ uses the chain rule formula and the derivative formula for the trigonometric function.
By applying the product rule formula with $latex u’$ and $latex v’$, we have:
$$\frac{d}{dx}f(x) = 5x^7 \cdot (-7x^6 \csc^{2}{(x^7)}) + \cot{(x^7)} \cdot (35x^6)$$
Simplifying algebraically, we get
$$ \frac{d}{dx}f(x) = -35x^{13} \csc^{2}{(x^7)} + 35x^6 \cot{(x^7)}$$
And the final answer is:
$$f'(x) = 35x^6 \cot{(x^7)} – 35x^{13} \csc^{2}{(x^7)}$$
EXAMPLE 5
What is the derivative of $latex f(x) = x^7 \sin{(\sin^{-1}{(x)})}$?
Solution
Here, the first multiplicand is $latex u=x^7$ and the second multiplicand is $latex v=\sin{(\sin^{-1}{(x)})}$.
Therefore, we have
$latex u = x^7$
$latex v = \sin{(\sin^{-1}{(x)})}$
$latex f(x) = uv$
Now, we use the product rule formula to derive our given problem:
$latex f'(x) = uv’ + vu’$
$$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$$
$$\frac{d}{dx}f(x) = x^7 \cdot \frac{d}{dx}(\sin{(\sin^{-1}{(x)})})+ \sin{(\sin^{-1}{(x)})} \cdot \frac{d}{dx}(x^7)$$
Note: In this problem, we derive $latex u$ using the power rule formula and derive $latex v$ using the derivative formulas for the trigonometric function and the inverse trigonometric function.
Applying the product rule formula, we have:
$$\frac{d}{dx}f(x) = x^7 \cdot (\cos{(\sin^{-1}{(x)})} (\frac{1}{\sqrt{1-x^2}}))+ \sin{(\sin^{-1}{(x)})} \cdot (7x^6)$$
Simplifying algebraically and applying identities and trigonometric and inverse trigonometric operations, we get
$$\frac{d}{dx}f(x) = x^7 \cdot (1) + 7x^6 \cdot (x)$$
And the final answer is:
$latex f'(x) = 8x^7$
Product Rule – Practice Problems
Find the derivative of the following function and determine the value of $latex F^{\prime}(0)$: $latex F(x) = \sin(x^2+2x)\cos(x)$?
Write the answer in the input box
See also
Interested in learning more about the Product Rule? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
