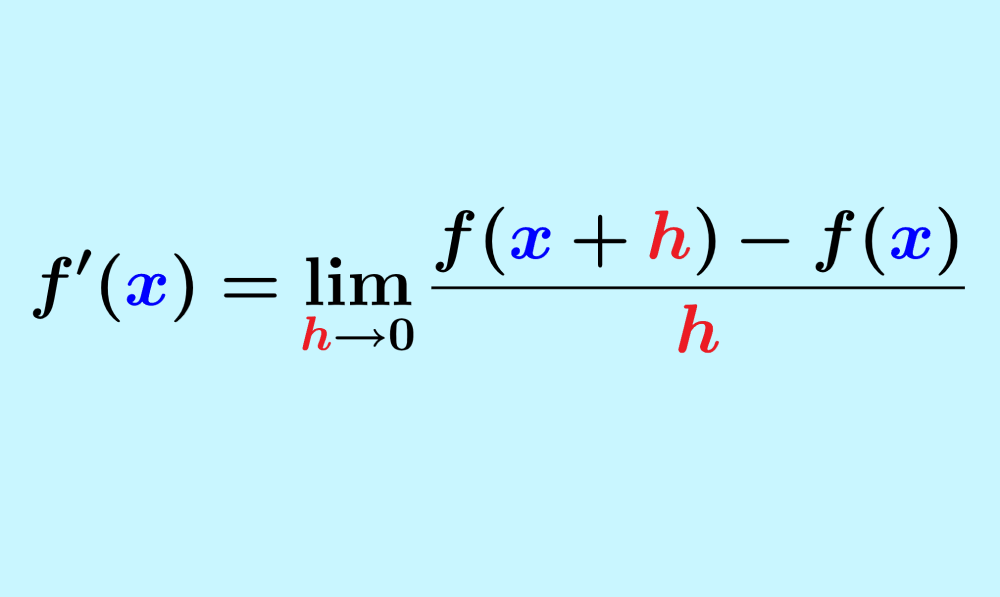The definition of the derivative as a limit can be found by using the slope formula to find the slope of the secant line between two points on the function. We then use a limit to bring the points closer together so that the slope of the secant is an approximation to the slope of the tangent.
Here, we will learn about the definition of the derivative as a limit. We will use a diagram to find this definition step by step. Then we will apply this idea to find the derivatives of some functions.
How to define the derivative using limits
We are going to use limits to find an equation that allows us to find the slope of the tangent line to a function. For this, we use the following diagram:
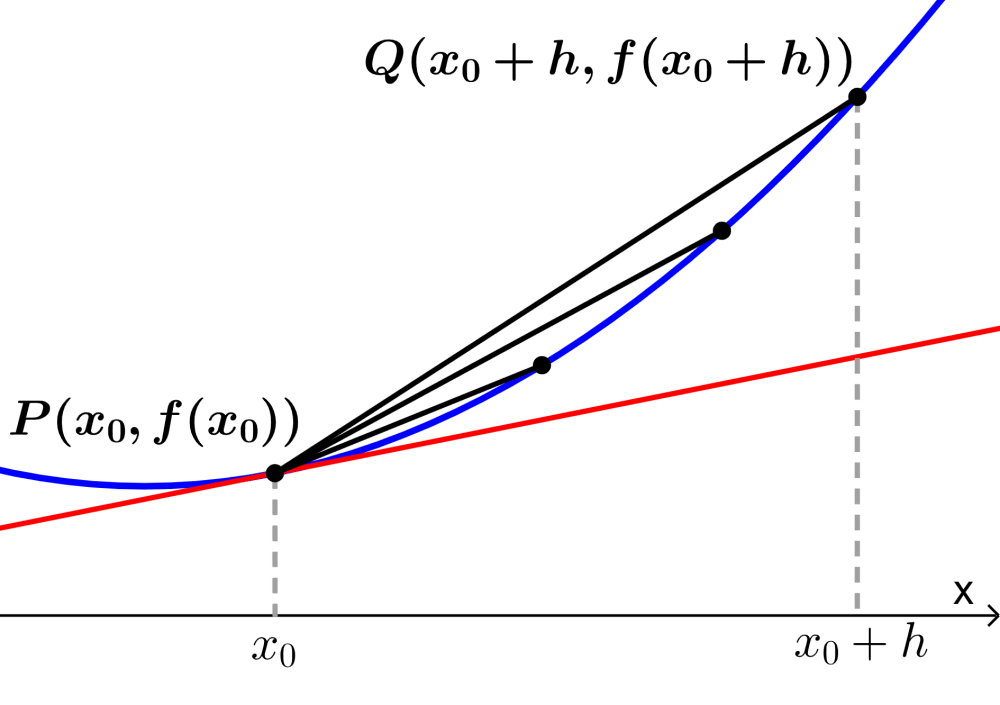
Consider the point $latex P~(x_{0},~ f(x_{0}))$ that lies on the curve produced by the function $latex f(x)$, as shown in the diagram. We are going to find the slope of the tangent line to f at the point P.
We can find the slope using the point $latex Q~(x_{0}+h,~f(x_{0}+h)$, which is h units from P, and we assume that h is very small.
Therefore, we start by calculating the slope of the secant line PQ. We know that the slope is equal to the change in y over the change in x. Thus, we have:
$$\text{Slope of PQ}=\frac{f(x_{0}+h)-f(x_{0})}{x_{0}+h-x_{0}}$$
$$\text{Slope of PQ}=\frac{f(x_{0}+h)-f(x_{0})}{h}$$
If h is small enough, point Q will get closer and closer to P until the slope of the secant line PQ will be a good approximation for the slope of the tangent line at P.
Therefore, we define the slope of the tangent line to be the limit of the slope of the secant line as h approaches 0:
$$m_{tan}=\lim _{h \to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$$
Now, instead of using the constant $latex x_{0}$, we can use the variable $latex x$. Thus, the resulting limit will be an expression in terms of x.
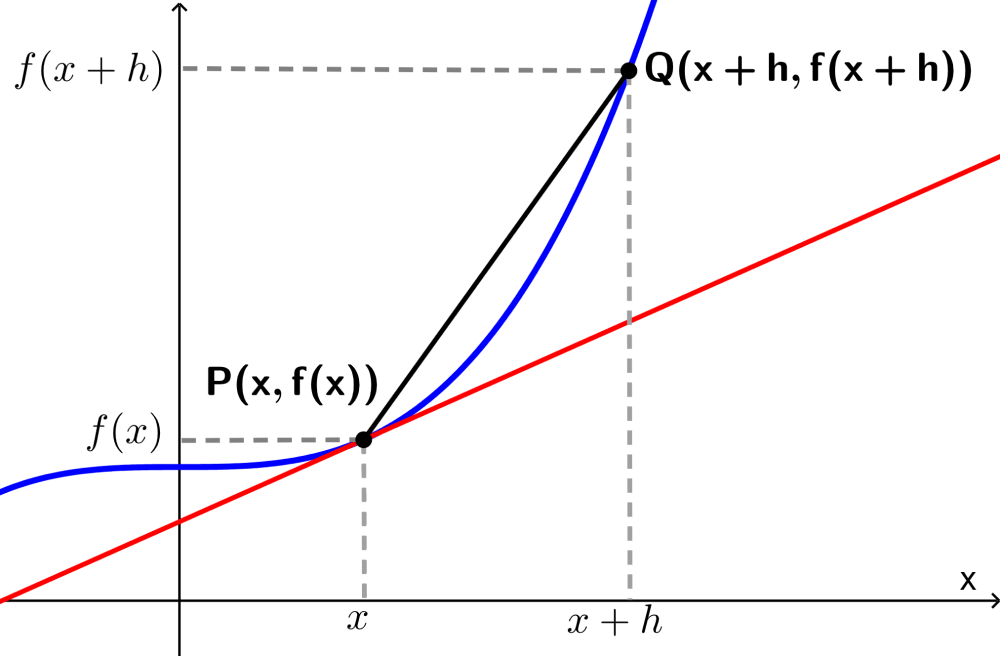
This expression can be considered as a function of x. Furthermore, this function, which can be denoted by $latex f'(x)$, is the derivative of the function f.
Therefore, if we have that $latex f(x)$ is a function of x, the derivative of f at x is:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Derivatives as a rate of change
The derivative of a function $latex f(x)$ at x is the instantaneous rate of change of the function at x. This is because the derivative is defined as the limit, which finds the slope of the tangent line to a function.
Recall that the slope represents the change in y over the change in x. That is, we have a rate of change with respect to x.
If $latex y=f(x)$ is a function of x, then we can also use the notation $latex \frac{dy}{dx}$ to represent the derivative of f.
$latex \frac{dy}{dx}$ is the derivative of y with respect to x. That is, this is the rate at which y changes when x changes.
For example, if $latex d(t)$ represents the displacement of a car in time t, then $latex d~'(t)$ represents the speed of the car in time t. If $latex y=f(x)$ is a function of x, then $latex f'(x)$ represents how y changes when x changes.
If $latex f'(x)$ is positive at a certain point, then y increases as x increases. If $latex f'(x)$ is negative at some point, then y decreases as x increases.
Examples of derivatives using limits
The following are some examples of how to find the derivative of a function using its definition as limits.
EXAMPLE 1
Find the derivative of $latex f(x)=10x$ using the definition of derivative as a limit.
Solution: A derivative can be found using the following formula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Therefore, we use the function $latex f(x)=10x$ on the numerator, and we have:
$$f'(x)=\lim _{h \to 0}\frac{10(x+h)-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10x+10h-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10h}{h}$$
Simplifying the h in the numerator with the h in the denominator, we have:
$$f'(x)=\lim _{h \to 0}(10)$$
Since we don’t have any h, we simply remove the limit:
$latex f'(x)=10$
EXAMPLE 2
Find the derivative of $latex f(x)=3x^2$ using the definition of the derivative with limits.
Solution: We use the formula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Then, we rewrite the numerator using $latex f(x)=3x^2$ and we have:
$$f'(x)=\lim _{h \to 0}\frac{3(x+h)^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2+6hx+3h^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6hx+3h^2}{h}$$
We can factor out the h from the numerator and simplify with the denominator:
$$f'(x)=\lim _{h \to 0}\frac{h(6x+3h)}{h}$$
$$f'(x)=\lim _{h \to 0}(6x+3h)$$
Finally, we solve the limit by substituting $latex h=0$ into the expression:
$latex f'(x)=6x+3(0)$
$latex f'(x)=6x$
EXAMPLE 3
Find the derivative of $latex f(x)=5x^2+6x$ using limits.
Solution: The formula for the derivative of a function using limits is:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Therefore, using the function $latex f(x)=5x^2+6x$ on the numerator, we have:
$$f'(x)=\lim _{h \to 0}\frac{(5(x+h)^2+6(x+h))-(5x^2+6x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5(x^2+2hx+h^2)+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5x^2+10hx+5h^2+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10hx+5h^2+6h}{h}$$
We factor the h of the numerator to simplify with the h of the denominator:
$$f'(x)=\lim _{h \to 0}\frac{h(10x+5h+6)}{h}$$
$$f'(x)=\lim _{h \to 0}(10x+5h+6)$$
Finally, we solve the limit by substituting $latex h=0$ into the expression:
$latex f'(x)=10x+5(0)+6$
$latex f'(x)=10x+6$
See also
Interested in learning more about derivatives of functions? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
