The coordinates of the inflection points of a function are found using the derivative of the function. Therefore, we have to find the roots of the derivative, and then we analyze the nature of these points. At the inflection points, the slope has the same sign on both sides of the point.
Here, we will learn about inflection points of functions. We will learn how to find these points and solve some practice exercises.
What are the inflection points of a function?
The inflection points of a function are stationary points that have the main characteristic that the slope has the same sign on both sides of the point.
The stationary points of functions are the points where the slope is equal to zero. This means that at the inflection points, we have $latex \frac{dy}{dx}=0$.
In the following diagram, we can observe the two cases of inflection points:
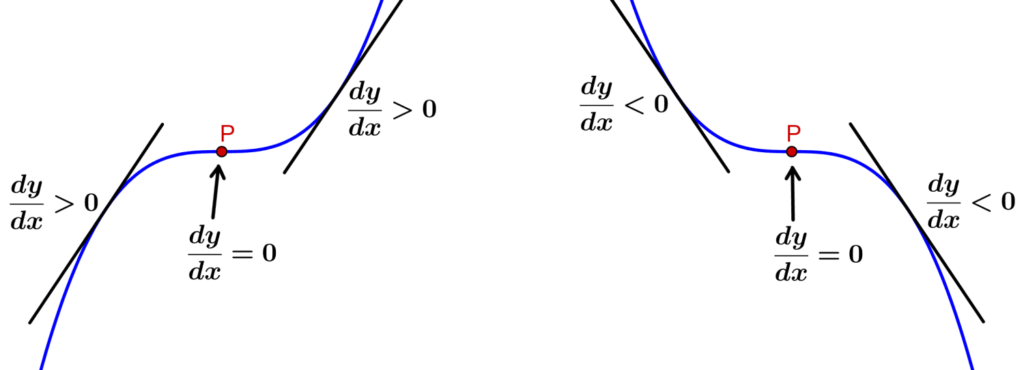
At the inflection point on the left, the slope is positive on both sides of the inflection point. That is, the function grows from left to right, so we have the following:
- On the left-hand side of P: $latex \frac{dy}{dx}>0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}>0$
At the inflection point on the right, the slope is negative on both sides of the inflection point. That is, the function decreases from left to right, so we have the following:
- On the left-hand side of P: $latex \frac{dy}{dx}<0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}<0$
How to find the inflection points of a function?
To find the inflection points, we use the derivative of the function to find the stationary points. Then, we can classify the inflection points with the second derivative or with the signs of the derivative on each side of the point.
Recall that stationary points are characterized in that the slope at those points is equal to zero. Thus, we use the derivative of the function to form an equation and find its roots.
We follow the following steps to find the inflection points of a function:
Step 1: Get the derivative of the function.
Step 2: Find the stationary points using the derivative. For this, we form the equation $latex \frac{dy}{dx}=0$ and find the values of x.
Step 3: Determine which of the stationary points are points of inflection. When we have an inflection point, we should have $latex \frac{d^2y}{dx^2}=0$.
However, the second derivative could also be zero at a maximum or minimum point. Therefore, the best way to identify inflection points is to examine the sign of the derivative on each side of the point.
For a stationary point to be an inflection point, the slope must have the same sign on both sides of the point.
Step 4: Use the x-coordinates of the inflection points to find the y-coordinates of the points.
Inflection points of a function – Examples with answers
EXAMPLE 1
Find the inflection point of the function $latex f(x)=x^3+2$.
Solution
Step 1: The derivative of the function is:
$latex f(x)=x^3+2$
$latex f'(x)=3x^2$
Step 2: Using the derivative, we form an equation and find the values of x:
$latex 3x^2=0$
$latex x=0$
Step 3: We use the second derivative to verify that the point is an inflection point:
$latex f^{\prime \prime}(x)=6x$
When $latex x=0$, we have $latex f^{\prime \prime}(x)=0$. Therefore, the point is an inflection point. We can use your graph to fully verify:
Step 4: Using $latex x=0$ in the function, we find the y-coordinate of the point:
$latex y=x^3+2$
$latex y=(0)^3+2$
$latex y=2$
The coordinates of the inflection point are (0, 2).
EXAMPLE 2
What are the coordinates of the inflection point of the function $latex f(x)=x^5-4$?
Solution
Step 1: Start by finding the derivative of the function:
$latex f(x)=x^5-4$
$latex f'(x)=5x^4$
Step 2: Find the values of x in the equation formed by the derivative:
$latex 5x^4=0$
$latex x=0$
Step 3: Check if the point is an inflection point using the second derivative:
$latex f^{\prime \prime}(x)=20x^3$
When $latex x=0$, we have $latex f^{\prime \prime}(x)=0$. Thus, the point is a turning point. We can use its graph to fully verify:
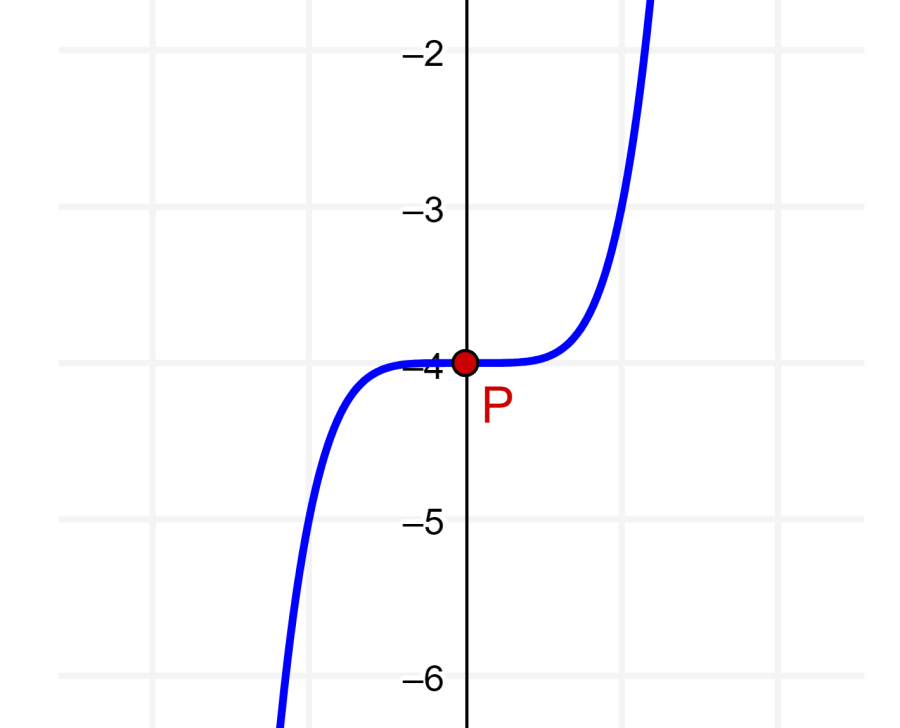
Step 4: Find the y-coordinate of the point using $latex x=0$ in the function:
$latex y=x^5-4$
$latex y=(0)^5-4$
$latex y=-4$
The coordinates of the inflection point are (0, -4).
EXAMPLE 3
Find the inflection point of the function $latex f(x)=x^3-9x^2+27x-29$.
Solution
Step 1: Start by finding the derivative of the function:
$latex f(x)=x^3-9x^2+27x-29$
$latex f'(x)=3x^2-18x+27$
Step 2: Form an equation with the derivative to find the x-values of the stationary points:
$latex 3x^2-18x+27=0$
$latex 3(x^2-6x+9)=0$
$latex 3(x-3)(x-3)=0$
$latex x=3$
Step 3: Check if the point is an inflection point with the second derivative:
$latex f^{\prime \prime}(x)=6x-18$
When $latex x=3$, we have $latex f^{\prime \prime}(x)=0$.
Also, when we use $latex x=3.1$ (to the right of the point) and $late x=2.9$ (to the left of the point) in the first derivative, we get two positive values, thus confirming that it is an inflection point.
Step 4: Using $latex x=3$ in the function, we find the y-coordinate of the point:
$latex y=x^3-9x^2+27x-29$
$latex y=(3)^3-9(3)^2+27(3)-29$
$latex y=-2$
The coordinates of the inflection point are (3, -2).
EXAMPLE 4
Find the coordinates of the inflection point of the function $latex f(x)=x^4+4x^3+1$.
Solution
Step 1: Differentiating the function, we have:
$latex f(x)=x^4+4x^3+1$
$latex f'(x)=4x^3+12x^2$
Step 2: The values of x of the stationary points are:
$latex 4x^3+12x^2=0$
$latex 4x^2(x+3)=0$
$latex x=0~~$ or $latex ~~x=-3$
Step 3: We use the second derivative to determine which point is an inflection point:
$latex f^{\prime \prime}(x)=12x^2+24x$
When $latex x=0$, we have $latex f^{\prime \prime}(x)=0$ and when $latex x=-3$, we have $latex f^{\prime \prime}(x)> 0$. Then, the point $latex x=0$ could be a turning point.
By using the values $latex x=0.1$ and $latex x=-0.1$ in the first derivative, we get slopes with the same sign, so the point is indeed an inflection point.
Step 4: Using $latex x=0$ in the function, we find the y-coordinate of the point:
$latex y=x^4+4x^3+1$
$latex y=(0)^4+4(0)^3+1$
$latex y=1$
The coordinates of the inflection point are (0, 1).
EXAMPLE 5
What are the inflection points of the function $latex f(x)=x^4 – 4x^2 + 4$?
Solution
The derivative and the second derivative of the function are:
$latex f(x)=x^4 – 4x^2 + 4$
$latex f^{\prime}(x)=4x^3-8x$
$latex f^{\prime \prime}(x)=12x^2-8$
Now, we use the second derivative to form an equation and find the values of x:
$latex f^{\prime \prime}(x)=12x^2-8=0$
$$x^2=\frac{2}{3}$$
$$x=\pm \sqrt{\frac{2}{3}}$$
Therefore, the inflection points occur at the points $latex x=\pm \sqrt{\frac{2}{3}}$.
Now, we use these x values to find the y coordinates:
$$y_{1}=\left(\sqrt{\frac{2}{3}}\right)^4 – 4\left(\sqrt{\frac{2}{3}}\right)^2 + 4$$
$$y_{1}=\frac{4}{3}$$
$$y_{2}=\left(-\sqrt{\frac{2}{3}}\right)^4 – 4\left(-\sqrt{\frac{2}{3}}\right)^2 + 4$$
$$y_{2}=\frac{4}{3}$$
The coordinates of the inflection points are $latex \left(\sqrt{\frac{2}{3}}, \frac{4}{3}\right)$ and $latex \left(-\sqrt{\frac{2}{3}}, \frac{4}{3}\right)$.
Points of inflection of a function – Exercises to solve
What are the coordinates of the inflection point in the function $latex f(x)=x^3-3x^2+x$?
Write the coordinates in the input box.
See also
Interested in learning more about derivatives and stationary points? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
