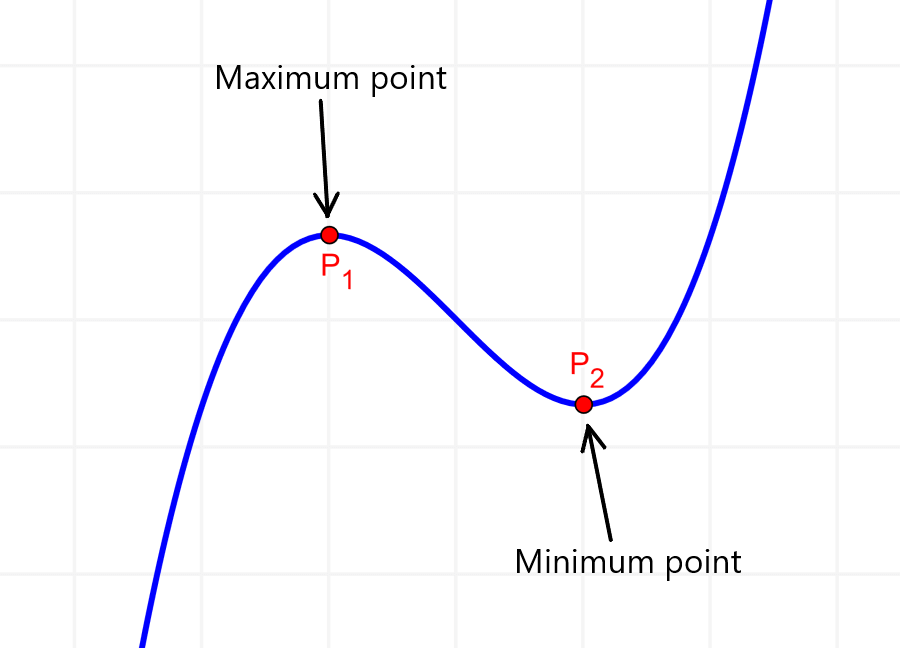
The maxima, minima, and inflection points are called stationary points of a function. The coordinates of these points can be found using the derivative of the function. The slope at the maxima, minima, and inflection points is equal to zero. Thus, we have to find the roots of the derivative.
Here, we will learn about maxima, minima, and inflection points of functions. In addition, we will learn how to find the coordinates of these points with examples.
- Definition of the maximum point of a function
- Finding the coordinates of the maximum point of a function
- Definition of the minimum point of a function
- Finding the coordinates of the minimum point of a function
- Defining the inflection points of a function
- Finding the coordinates of the inflection points of a function
- See also
Definition of the maximum point of a function
The maximum points of functions are points where the values of y of the function are the highest possible that the functions can reach. That is, there is no other point in the function that has a greater value of y.
The maximum point of a function is one of the stationary points of the function. At these points, the slope of the tangent line is equal to zero. That means we have $latex \frac{dy}{dx}=0$.
The following diagram shows a graphical representation of a maximum point of a function:
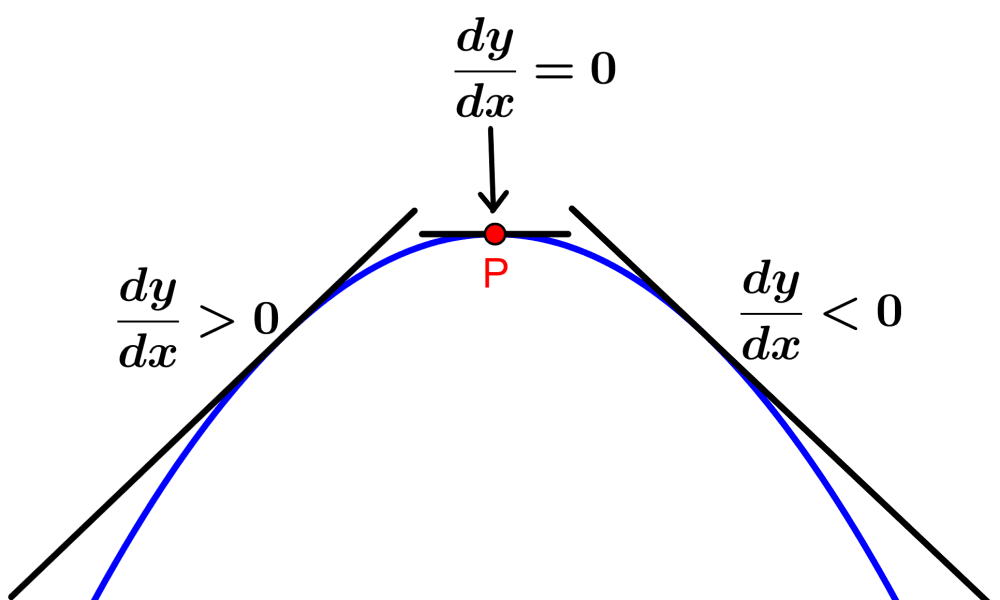
To the left of a maximum point, the slope is positive and to the right of the maximum point, the slope is negative. That is, the function increases until it reaches the maximum point and then decreases. Then, we have:
- On the left-hand side of P: $latex \frac{dy}{dx}>0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}<0$
Since the slope (the value of the derivative) goes from positive to negative near the maximum point, the second derivative of the function at a maximum point is negative (the first derivative decreases).
Finding the coordinates of the maximum point of a function
We can find the coordinates of a maximum point by using the derivative of the function. For this, we consider that the slope at a maximum point is equal to zero.
Therefore, we form an equation with the derivative and find its roots (the x values). We then use the second derivative to identify which of those values is the maximum point.
If we know the function, we can find its maximum point with the following steps:
Step 1: Calculate the derivative of the function.
Step 2: Find the stationary points with the derivative. To do this, we form an equation with the derivative and solve for x. That is, we have $latex \frac{dy}{dx}=0$.
Step 3: Determine which of the points from step 2 is the maximum point. For this, we use the second derivative.
When we have a maximum point, we must have $latex \frac{d^2y}{dx^2}<0$. That is, the second derivative at that point must be negative.
Step 4: Determine the y-coordinate of the maximum point using the x-coordinate from step 3.
EXAMPLE
Find the coordinates of the maximum point of $latex f(x)=\frac{1}{3}x^3+x^2-3x$.
Solution
Step 1: We start by finding the derivative of the function:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f'(x)=x^2+2x-3$
Step 2: Now, we use the derivative to find the stationary points:
$latex x^2+2x-3=0$
$latex (x+3)(x-1)=0$
$latex x=-3~~$ or $latex ~~x=1$
Step 3: We determine what the maximum point is using the second derivative:
$latex f^{\prime \prime}(x)=2x+2$
When $latex x=-3$, we have $latex f^{\prime \prime}(x)<0$ and when $latex x=1$, we have $latex f^{\prime \prime}(x)> 0$. So the maximum point is at $latex x=-3$.
Step 4: The y-coordinate of the maximum point is:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f(x)=\frac{1}{3}(-3)^3+(-3)^2-3(-3)$
$latex y=9$
The maximum point has the coordinates (-3, 9).
Definition of the minimum point of a function
The minimum points of functions are the points where the values of y of the function are the minimum possible. This means that there is no other point in the function that has a value of y less than the minimum point.
Minimum points are stationary points of a function. At these points, the slope of the tangent line is equal to zero. That is, at a minimum point we have $latex \frac{dy}{dx}=0$.
The following diagram is a graphical representation of a minimum point in a function:
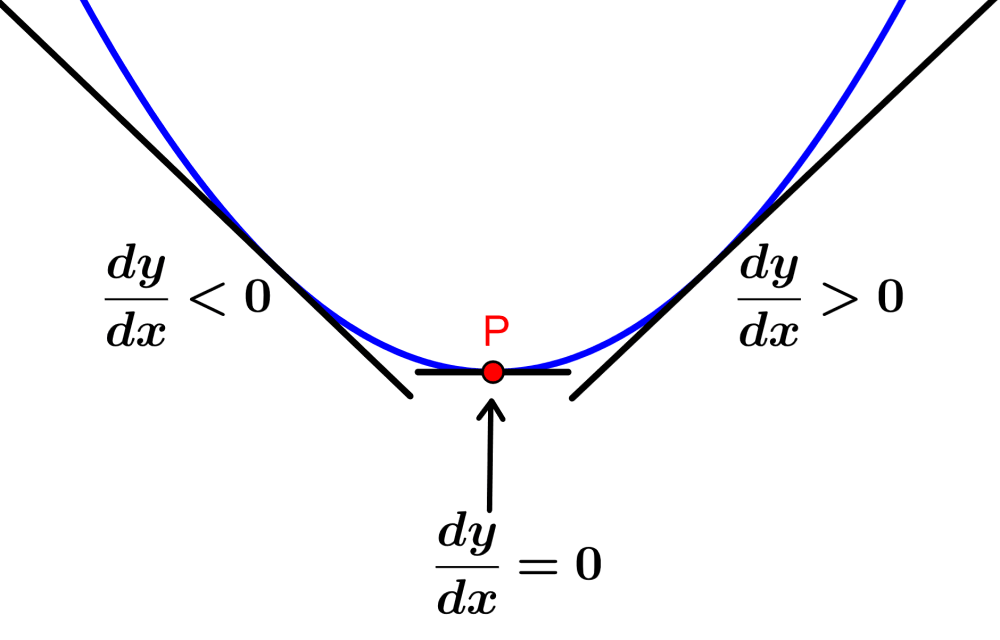
To the left of a minimum point, the slope is negative, and to the right of the minimum point, the slope is positive. That is, the function decreases until it reaches the minimum point and then increases. Then, we have:
- On the left-hand side of P: $latex \frac{dy}{dx}<0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}>0$
Since the slope (the value of the derivative) goes from negative to positive near the maximum point, the second derivative of the function at a minimum point is positive (the first derivative increases).
Finding the coordinates of the minimum point of a function
The coordinates of a minimum point of a function are found using the derivative of the function. We recall that at these points, the slope is equal to zero.
Therefore, we form an equation with the derivative and find its roots. Then, we use the second derivative to identify the minimum points.
If we know the function, we can follow these steps to determine its minimum point:
Step 1: Get the derivative of the function.
Step 2: Find the stationary points using the derivative. Thus, we form the equation $latex \frac{dy}{dx}=0$ and find the values of x.
Step 3: Use the second derivative to identify the minimum point. For a stationary point to be a minimum, we must have $latex \frac{d^2y}{dx^2}>0$.
Step 4: Use the x-coordinate from step 3 to find the y-coordinate of the minimum point.
EXAMPLE
What are the coordinates of the minimum point of the function $latex f(x)=2x^3-6x$?
Solution
Step 1: Start by finding the derivative of the function:
$latex f(x)=2x^3-6x$
$latex f'(x)=6x^2-6$
Step 2: Determine the values of x from the equation formed by the derivative:
$latex 6x^2-6=0$
$latex x=\sqrt{1}$
$latex x=\pm 1$
$latex x=1~~$ or $latex ~~x=-1$
Step 3: Use the second derivative to determine the nature of the stationary points found:
$latex f^{\prime \prime}(x)=12x$
When $latex x=1$, we have $latex f^{\prime \prime}(x)>0$ and when $latex x=-1$, we have $latex f^{\prime \prime}(x)< 0$. This means that $latex x=1$ is the minimum point.
Step 4: The y-coordinate of the minimum point is:
$latex y=2x^3-6x$
$latex y=2(1)^3-6(1)$
$latex y=-4$
The minimum point of the function is (1, -4).
Defining the inflection points of a function
The inflection points of a function are stationary points where the slope is equal to zero. That is, at an inflection point we have $latex \frac{dy}{dx}=0$.
The difference between inflection points and minimum or maximum points is that at inflection points, the slope has the same sign on both sides of the point.
In the following diagram, we can see a graphical representation of both cases of the inflection points of a function:
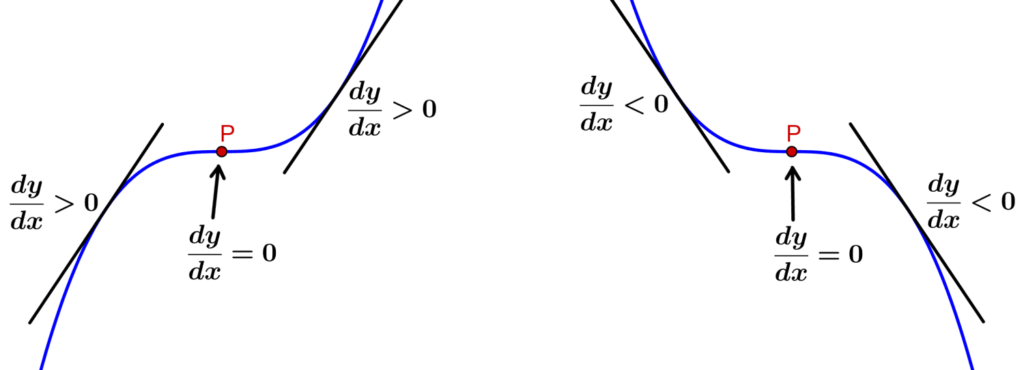
At the left inflection point, the function grows on both sides of the inflection point. That is, the slope is positive on both sides, so we have the following:
- On the left-hand side of P: $latex \frac{dy}{dx}>0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}>0$
At the inflection point on the right, the function decreases on both sides of the inflection point. That is, the slope is negative on both sides, so we have the following:
- On the left-hand side of P: $latex \frac{dy}{dx}<0$
- At point P: $latex \frac{dy}{dx}=0$
- On the right-hand side of P: $latex \frac{dy}{dx}<0$
Finding the coordinates of the inflection points of a function
The coordinates of the inflection points can be found using the derivative of the function. For this, we consider that the slope at the inflection points is equal to zero.
Therefore, we form an equation with the derivative of the function and find the values of x. Then, we use the second derivative to determine which of the points is an inflection point.
If we know the function, we can follow these steps to determine the coordinates of the inflection points:
Step 1: Calculate the derivative of the function.
Step 2: Use the derivative to find the stationary points of the function. For this, we form the equation $latex \frac{dy}{dx}=0$ and determine the values of x.
Step 3: Use the second derivative to identify points of inflection. When we have an inflection point, we should have $latex \frac{d^2y}{dx^2}=0$.
However, the maximum points or minimum points could also have a second derivative that is equal to zero. For this reason, we must check the signs on each side of the inflection points.
For a stationary point to be an inflection point, the slope must have the same sign on both sides of the point. That is, the derivative must have the same sign.
Step 4: Use the x-coordinates from step 3 to find the y-coordinates of the inflection points.
EXAMPLE
Find the coordinates of the inflection point of the function $latex f(x)=x^3-9x^2+27x-29$.
Solution
Step 1: The following is the derivative of the function:
$latex f(x)=x^3-9x^2+27x-29$
$latex f'(x)=3x^2-18x+27$
Step 2: Using the derivative, we find the stationary points:
$latex 3x^2-18x+27=0$
$latex 3(x^2-6x+9)=0$
$latex 3(x-3)(x-3)=0$
$latex x=3$
Step 3: We use the second derivative to determine if the point is an inflection point:
$latex f^{\prime \prime}(x)=6x-18$
When $latex x=3$, we have $latex f^{\prime \prime}(x)=0$.
Also, when we use $latex x=3.1$ (to the right of point) and $late x=2.9$ (to the left of point) in the first derivative, we get two positive values, thus confirming that it is an inflection point.
Step 4: The y-coordinate of the inflection point is:
$latex y=x^3-9x^2+27x-29$
$latex y=(3)^3-9(3)^2+27(3)-29$
$latex y=-2$
The coordinates of the inflection point are (3, -2).
See also
Interested in learning more about derivatives and stationary points? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
