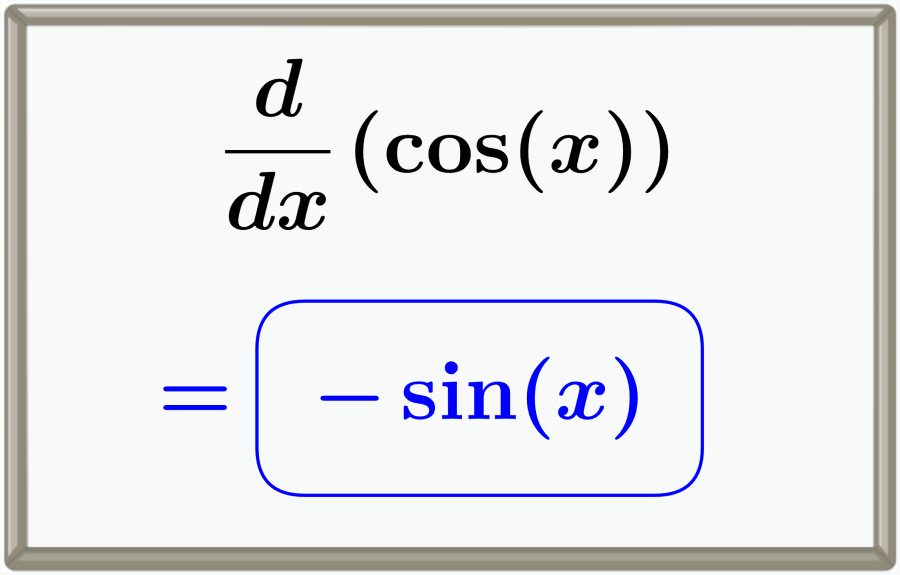The Derivative of Cosine is one of the main derivatives in Differential Calculus (or Calculus I). The derivative of cosine is equal to minus sine, -sin(x). This derivative can be proved using limits and trigonometric identities.
In this article, we will learn how to derive the trigonometric function cosine. We will explore its formula, see a graphical comparison of cosine and its derivative, and solve some examples.
Proof of the Derivative of the Cosine Function
The trigonometric function cosine of an angle is defined as the ratio of a side adjacent to an angle in a right triangle to the hypothenuse. Illustrating it through a figure, we have
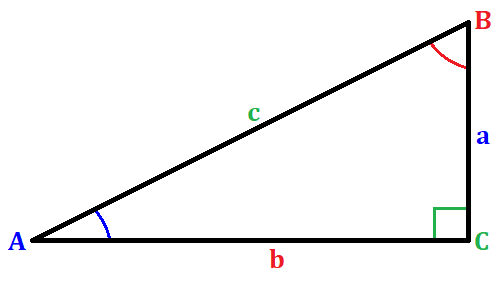
where C is 90°. For the sample right triangle, getting the cosine of angle A can be evaluated as
$latex \cos{(A)} = \frac{b}{c}$
where A is the angle, b is its adjacent side, and c is the hypothenuse of the right triangle in the figure.
Before learning the proof of the derivative of the cosine function, you are hereby recommended to learn the Pythagorean theorem, Soh-Cah-Toa & Cho-Sha-Cao, and the first principle of limits as prerequisites.
To review, any function can be derived by equating it to the limit of
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Suppose we are asked to get the derivative of
$latex f(x) = \cos{(x)}$
we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x+h)} – \cos{(x)} }{h}}$$
Analyzing our equation, we can observe that the first term in the numerator of the limit is a cosine of a sum of two angles x and h. With this observation, we can try to apply the sum and difference identities for cosine and sine, also called Ptolemy’s identities. Applying this, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x+h)} – \cos{(x)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ (\cos{(x)}\cos{(h)} – \sin{(x)}\sin{(h)}) – \cos{(x)} }{h}}$$
Let’s try to re-arrange the numerator
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}\cos{(h)} – \cos{(x)} – \sin{(x)}\sin{(h)} }{h}}$$
Factoring the first and second terms of our re-arranged numerator, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}(\cos{(h)} – 1) – \sin{(x)}\sin{(h)}) }{h}}$$
Doing some algebraic re-arrangements, we have
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)} (-(1-\cos{(h)})) – \sin{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ -\cos{(x)} (1-\cos{(h)}) – \sin{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \left( \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} – \frac{ \sin{(x)}\sin{(h)} }{h} \right) }$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} } – \lim \limits_{h \to 0} { \frac{ \sin{(x)}\sin{(h)} }{h} }$$
Since we are calculating the limit in terms of h, all functions that are not h will be considered as constants. Re-arranging, we have
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{(h)} }{h} } \right)$$
In accordance with the limits of trigonometric functions, the limit of trigonometric function $latex \cos{(\theta)}$ to $latex \theta$ as $latex \theta$ approaches zero is equal to one. The same can be applied to $latex \cos{(h)}$ over $latex h$. Applying, we have
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)} \cdot 1$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)}$$
We have already evaluated the limit of the last term. However, the first term is still impossible to be definitely evaluated due to the denominator $latex h$. Let’s try to use another trigonometric identity and see if the trick will work.
We may try to use the half-angle identity in the numerator of the first term.
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \left(2\sin^{2}{\left(\frac{h}{2}\right)}\right) }{h} } \right) – \sin{(x)}$$
Applying the rules of fraction to the first term and re-arranging algebraically once more, we have,
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \frac{\sin^{2}{\left(\frac{h}{2}\right)}}{1} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin^{2}{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{\left(\frac{h}{2}\right)} \cdot \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } }\right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot \left( \frac{ \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } \right) }\right) – \sin{(x)}$$
As you notice once more, we have a sine of a variable over that same variable. In this case, it is $latex \sin{\left(\frac{h}{2}\right)}$ all over $latex \frac{h}{2}$. Hence, we can apply again the limits of trigonometric functions of $latex \frac{\sin{(\theta)}}{\theta}$.
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot 1} \right) – \sin{(x)}$$
Finally, we have successfully made it possible to evaluate the limit of the first term. Evaluating by substituting the approaching value of $latex h$, we have
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} }\right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{0}{2}\right)}} \right) – \sin{(x)}$$
$$ \frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{(0)}} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} {0} \right) – \sin(x)$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \cdot 0 – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)}$$
Therefore, the derivative of the trigonometric function ‘cosine‘ is:
$$\frac{d}{dx} (\cos{(x)}) = -\sin{(x)}$$
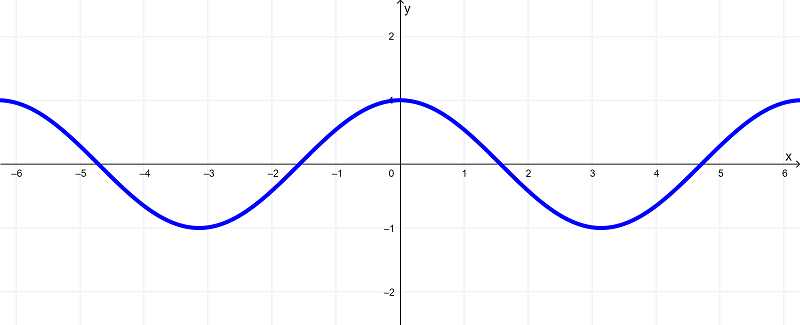
Graph of Cosine x VS. The Derivative of Cosine x
The graph of the function
$latex f(x) = \cos{(x)}$
is
By deriving the function $latex f(x) = \cos(x)$, we get
$latex f'(x) = -\sin{(x)}$
which is illustrated graphically as
Illustrating both graphs in one, we have
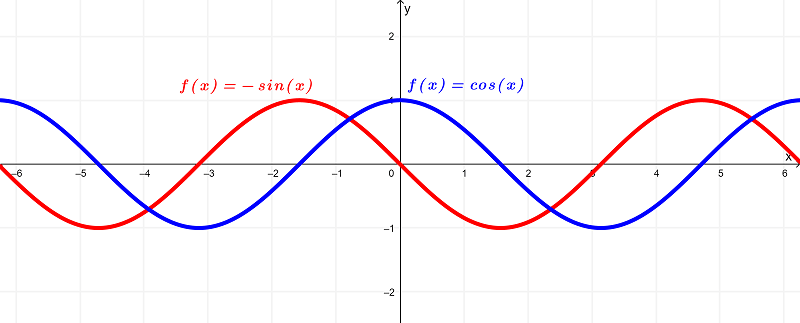
Analyzing these functions through these graphs, we see that the original function $latex f(x) = \cos(x)$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex [-1,1]$
whereas the derivative $latex f'(x) = -\sin{(x)}$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex [-1,1]$
Examples
Here are some examples of how to find the derivative of a composite cosine function using the chain rule:
EXAMPLE 1
Find the derivative of $latex f(x) = \cos(6x)$
Solution
The given cosine function is a composite function, where $latex 6x $ is an inner function. This means that we have to use the chain rule.
If we consider $latex u=5x$ as the inner function, we have $latex f(u)=\cos(u)$. Then, using the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\sin(u) \times 6$$
Substituting $latex u=6x$ back into the function, we have:
$$\frac{dy}{dx}=-6\sin(6x)$$
EXAMPLE 2
What is the derivative of $latex F(x) = \cos(4x^2+5 )$?
Solution
We have a composite cosine function, so we’re going to use the chain rule.
We can express the cosine function as $latex f (u) = \cos(u)$, where $latex u = 4x^2+5$.
Then, the derivative of the outer function $latex f(u)$ is:
$$\frac{d}{du} ( \cos(u)) = -\sin(u)$$
Now, we find the derivative of the inner function $latex g(x)$ or $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(4x^2+5)$$
$$\frac{d}{dx}(g(x)) = 8x$$
The chain rule tells us that we multiply the derivative of the outer function $latex f(u)$ by the derivative of the inner function $latex g(x)$. Then,
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\sin(u) \cdot 8x$$
Finally, we substitute $latex u$ into $latex f'(u)$ and simplify:
$$\frac{dy}{dx} = -\sin(4x^2+5) \cdot 8x$$
$$\frac{dy}{dx} = -8x\sin(4x^2+5)$$
EXAMPLE 3
Derive the function $latex f(x) = \cos(\sqrt{x})$
Solution
To use the chain rule, we consider $latex u=\sqrt{x}$ as the inner function.
We then rewrite $latex u=\sqrt{x}$ as $latex u=x^{\frac{1}{2}}$ to make the problem easier. This means that, the derivative $latex \frac{du}{dx}$ is:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Now, we write $latex f(u)=\cos(u)$ and using the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\sin(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Using $latex u=\sqrt{x}$ and simplifying, we have:
$$\frac{dy}{dx}=-\sin(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}}\sin(\sqrt{x})$$
Practice of derivatives of composite cosine functions
See also
Interested in learning more about the derivatives of trigonometric functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
