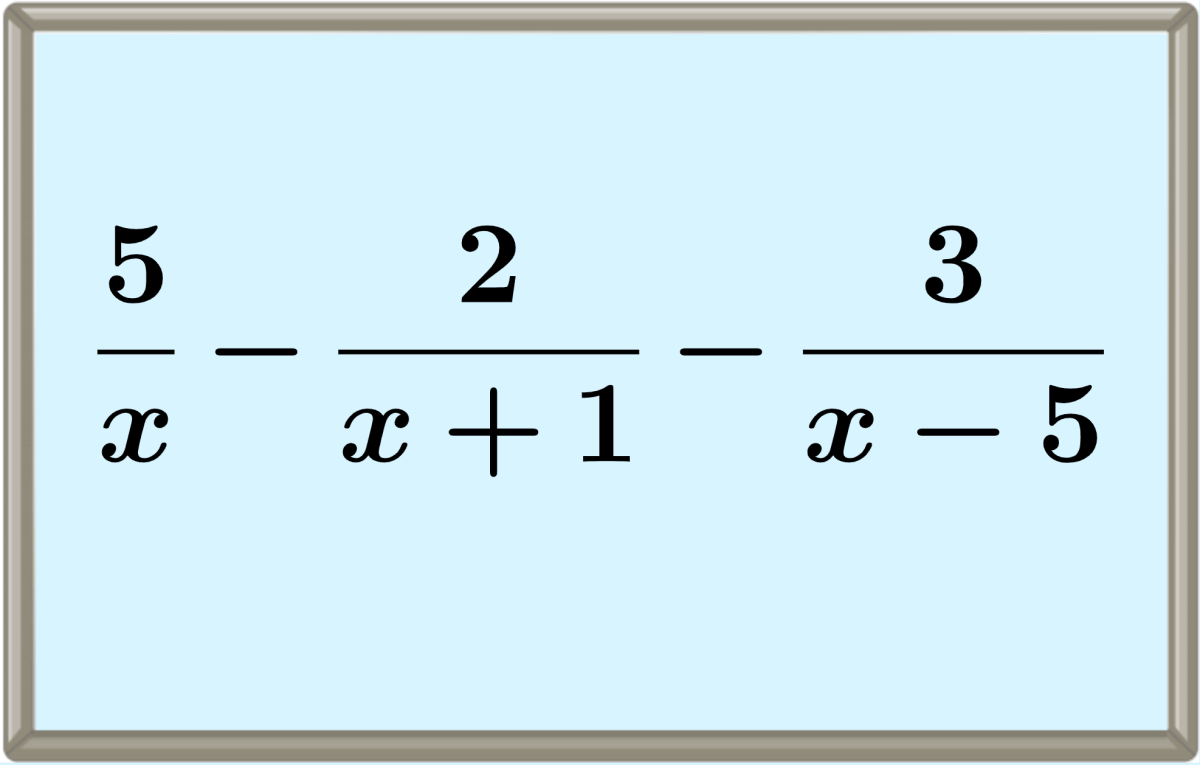Subtracting Algebraic Fractions – Examples and Practice

In this case, both fractions have the same denominator $latex b$. That is to say, we are dealing with two fractions with a common denominator $latex b$.

Since we are dealing with fractions with common denominator, the resulting fraction will be the subtraction of the numerators divided by the common denominator, which in this example is $latex b$.

$$\frac{a}{b} – \frac{c}{b} = \frac{a – c}{b}$$

The result is:

$$ \frac{a – c}{b}$$

We propose the operation to be performed:

$$ \frac{3x}{5} – \frac{2x}{5}$$

We notice again that it is a subtraction of two fractions with a common denominator, 5.

The resulting fraction is obtained by subtracting the numerators and dividing by the common denominator:

$$ \frac{3x}{5} – \frac{2x}{5} = \frac{3x – 2x}{5}$$

$$ = \frac{x}{5}$$

The result is:

$$\frac{x}{5}$$

Unlike the previous exercises, the two given fractions have different denominators.

The least common denominator (LCD) of both is $latex yz $.

If we multiply the numerator and denominator of the first fraction by z we have a fraction equivalent to the original one:

$$ \frac{2xz}{yz}$$

Similarly, multiplying the numerator and denominator of the second by y gives the equivalent fraction:

$$ \frac{xy}{zy}$$

We subtract the equivalent fractions:

$$ \frac{2xz}{yz} – \frac{xy}{zy}$$

Since $latex yz = zy$ the above expression is equivalent to:

$$ \frac{2xz}{yz} – \frac{xy}{yz}$$$.

Now we have the subtraction of two fractions with the common denominator yz. The resulting fraction is the subtraction of the numerators, divided by the common denominator.

$$ \frac{2xz}{yz} – \frac{xy}{yz}= \frac{2xz – xy}{yz}$$

The result is:

$$\frac{2xz – xyz}{yz}$$

This is a difference of two fractions with different denominators. Their lowest common denominator is 3×2=6.

Then the following procedure is followed to obtain the subtraction of two fractions equivalent to the original ones, but with the denominator equal for both:

• We multiply both the numerator and the denominator of the first fraction by 2 to get $latex{4x}{6}$.
• We multiply both the numerator and the denominator of the second fraction by 3 to get $latex{3x}{6}$.

Now, we have the following:

$$\frac{2x}{3}-\frac{x}{2}= \frac{4x}{6}-\frac{3x}{6}$$

$$ = \frac{4x-3x}{6}$$

$$ = \frac{x}{6}$$

The result is: $latex \frac{x}{6}$.

The denominators are: 6 and 4, that is 2×3 and 2×2. This means that their lowest common denominator is 12 (common and uncommon with their greatest exponent).

$$ \frac{a-2}{6} – \frac{3a+2}{4} = \frac{2(a-2)}{12}-\frac{3(3a+2)}{12}$$

$$= \frac{2a-4}{12} – \frac{9a+6}{12}$$

$$= \frac{(2a-4)-(9a+6)}{12} $$

$$= \frac{2a-4-9a-6}{12}$$

$$=\frac{-7a-10}{12}$$

$$= – \frac{7a+10}{12}$$

The result is: $latex – \frac{7a+10}{12}$.

They are fractions of non-common denominators. We will apply the following procedure, which we will call cross multiplication:

To find the resulting numerator, multiply the numerator of the first by the denominator of the second MINUS the denominator of the first by the numerator of the second.

The resulting denominator is the product of the denominators.

$$ \frac{2}{x-4} – \frac{1}{x-3} = \frac{2(x-3) – 1(x-4)}{(x-4)(x-3)}$$

$$ = \frac{2x-6-x+4}{(x-4)(x-3)} $$

The result is:

$$ \frac{x-2}{(x-4)(x-3)} $$

The result is:

$$ \frac{(m-n)^2 – (m+n)^2}{(m+n)(m-n)}$$

If the factors are expanded, an equivalent result is obtained:

$$ =\frac{m^2-2mn+n^2-m^2-2mn-n^2}{m^2-mn+nm-n^2}$$

$$= \frac{-4mn}{m^2-n^2}$$

If we multiply the numerator and denominator of the first fraction by 2, we have a subtraction of fractions with a common denominator:

$$\frac{2x-2}{8x+8} – \frac{x+2}{8x-8}$$

The numerator of the resulting fraction is the difference of numerators, and its denominator is the common denominator:

$$=\frac{(2x-2) – (x+2)}{8x+8}$$

Expanding the numerator:

$$=\frac{(2x-2-x-2)}{8x+8}$$

$$=\frac{(x-4)}{8x+8}$$

The result is:

$$\frac{(x-4)}{8(x+1)}$$

To find the solution, we will apply the method of multiplying in X explained in example 6.

$$\frac{a(a-1)^2 – (a^2-1)(a+1)}{(a^2-1)(a-1)^2}$$

The above result can be considered as the answer; however, if the numerator factors are expanded and simplified, an alternative result can be obtained:

$$=\frac{a(a^2-2a+1) – (a^3+a^2-a-1)}{(a^2-1)(a-1)^2}$$

$$=\frac{a^3-2a^2+a – (a^3+a^2-a-1)}{(a^2-1)(a-1)^2}$$

$$=\frac{a^3-2a^2+a – a^3-a^2+a+1}{(a^2-1)(a-1)^2}$$

which simplifies to the following result

$$=\frac{-3a^2+2a+1}{(a^2-1)(a-1)^2}$$

We will apply the method of multiplying in cross (X) explained in example 6.

$$ \frac{3}{x-1} – \frac{2}{x+1} = \frac{3(x+1) – 2(x-1)}{(x-1)(x+1)}$$

Now we expand the numerator and simplify as far as possible:

$$ =\frac{3x+3-2x+2}{(x-1)(x+1)}$$

The end result is:

$$ =\frac{(x+5)}{(x-1)(x+1)}$$