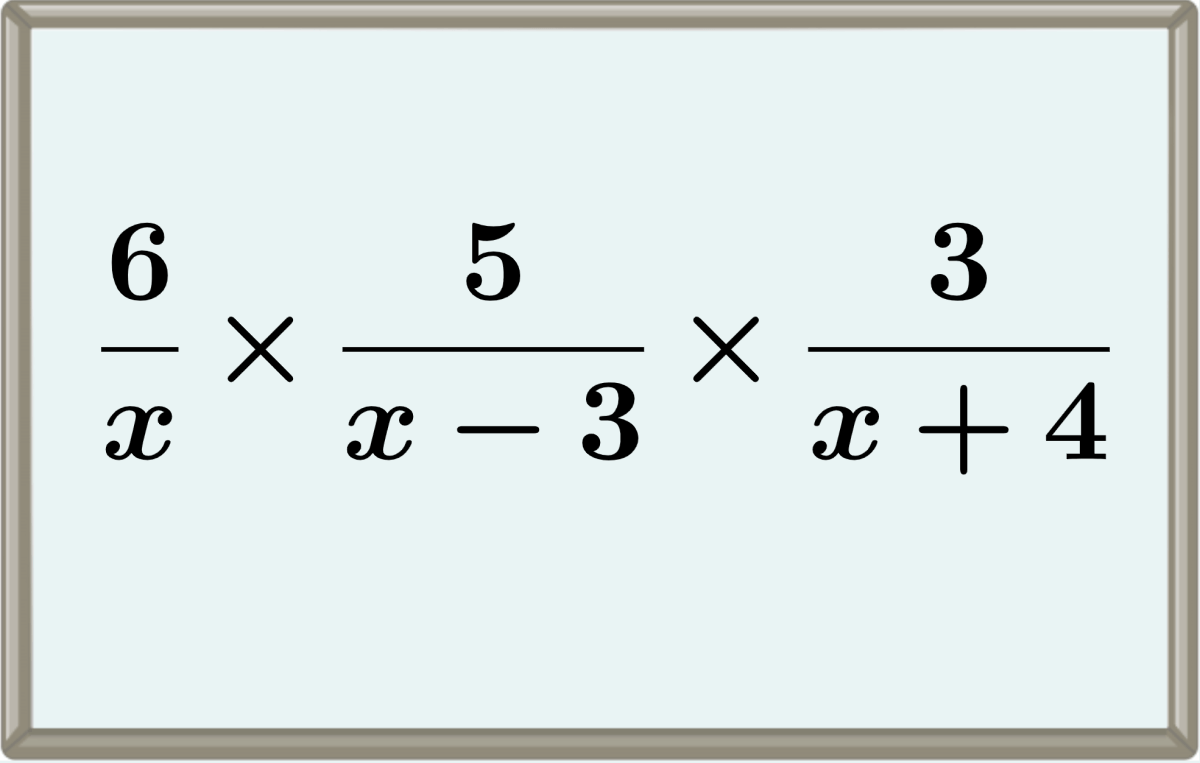To multiply two or more algebraic fractions, we simply multiply the numerators and denominators separately. Then, we simplify the resulting fraction by eliminating common factors in the numerator and denominator.
Here, we will look at some algebraic fraction multiplication exercises. In addition, we will explore practice problems to apply what we have learned.
How to multiply two or more algebraic fractions
Two or more algebraic fractions can be multiplied by multiplying their numerators and denominators separately.
For example, if we have the fractions $latex \frac{a}{b}$ and $latex \frac{x}{y}$, we can multiply them in the following way:
$$\frac{a}{b}\times \frac{x}{y}=\frac{a\times x}{b\times y}$$
Then, we can find the product of two or more algebraic fractions by following the steps below:
1. Multiply the numerators.
2. Multiply the denominators
3. Simplify the resulting fraction.
Reduce the common factors in the numerator and denominator.
Examples with answers on the product of algebraic fractions
EXAMPLE 1
Multiply the following algebraic fractions:
$$ \frac{2a}{3b^3} \times \frac{3b^2}{4a}$$
Solution
The fraction resulting from the product (or multiplication) of two algebraic fractions is the product of the numerators divided by the multiplication of their denominators:
$$ \frac{2a}{3b^3} \cdot \frac{3b^2}{4a} = \frac{(2a)\cdot (3b^2)}{(3b^3) \cdot (4a)}$$
Simplifying the common factors in the numerator and denominator, we are left with:
$$ =\frac{(1) \cdot (1)}{(b) \cdot (2)} $$
The end result is:
$$ \frac{1}{2b} $$
EXAMPLE 2
Find the result of the following product of algebraic fractions:
$$ \frac{7x+7}{10x+50} \cdot \frac{5x+25}{14} $$
Solution
Factor the numerator and denominator of each of the fractions shown:
$$ \frac{7(x+1)}{10(x+5)} \cdot \frac{5(x+5)}{2 \cdot 7} $$
Now, multiply numerator by numerator and denominator by denominator:
$$ \frac{7(x+1) \cdot 5(x+5)}{10(x+5) \cdot 2 \cdot 7} $$
We simplify or cancel common factors between the numerator and denominator:
$$ \frac{(x+1)}{2 \cdot 2 } $$
The end result is:
$$ \frac{(x+1)}{4} $$
EXAMPLE 3
Simplify as much as possible the following product of three algebraic fractions:
$$ \frac{10}{a} \cdot \frac{2a}{b^2} \cdot \frac{3b}{20} $$
Solution
Multiplying the numerators by each other and the denominators by each other:
$$ \frac{10 \cdot 2a \cdot 3b}{a \cdot b^2 \cdot 20} $$
Simplifying:
$$ \frac{1 \cdot 2 \cdot 3}{1 \cdot b \cdot 2} = \frac{1 \cdot 1 \cdot 3}{1 \cdot b \cdot 1} $$
The end result is:
$$ \frac{3}{b} $$
EXAMPLE 4
Find the product of the following fractions:
$$ \frac{x^3 + 2x^2 + x}{a^2 – b^2} \cdot \frac{a – b}{x^2 + x} $$
Solution
Numerators and denominators are multiplied together:
$$ \frac{(x^3 + 2x^2 + x)(a – b)}{(a^2 – b^2)(x^2 + x)} $$
The numerator and denominator are factored as much as possible:
$$ =\frac{x(x^2 + 2x + 1)(a – b)}{(a^2 – b^2)(x + 1)x} $$
We can factor the expression $latex x^2+2x+1$ recognizing that this is equal to $latex (x+1)^2$:
$$ =\frac{x(x+1)^2(a – b)}{(a^2 – b^2)(x + 1)x} $$
Using the difference of squares, we have:
$$ =\frac{x(x+1)^2(a – b)}{(a + b)(a – b)(x + 1)x} $$
Now we simplify or cancel like factors between numerator and denominator:
$$ =\frac{1(x+1)(1)}{(a + b)(1)(1)1} $$
Finally we are left with:
$$ \frac{(x+1)}{(a + b)} $$
EXAMPLE 5
Find the solution of the following product of algebraic fractions:
$$ \frac{a^2-4a – 5}{2a^2-50} \cdot \frac{2a-2}{3a+3} $$
Solution
Multiply the numerators by each other and the denominators by each other:
$$ \frac{(a^2-4a – 5)(2a-2)}{(2a^2-50)(3a+3)} $$
Substitute the first factor of the numerator, which is a quadratic polynomial by the product of two binomials:
$$ (a^2-4a – 5) = (a-5)(a+1) $$
and we take out the common factor wherever possible:
$$ \frac{(a-5)(a+1)2(a-1)}{(2(a^2-25))3(a+1)} $$
Apply the formula for the difference of squares in $latex (a^2-25)$:
$$ \frac{(a-5)(a+1)2(a-1)}{(2(a – 5)(a+5))3(a+1)} $$
We simplify
$$ \frac{(a-1)}{(a+5)3} $$
The end result is:
$$ \frac{(a-1)}{3(a+5)} $$
EXAMPLE 6
Determine the result of multiplying the algebraic expressions below. It is suggested that you first reduce them to algebraic fractions and then multiply them:
$$ (1 + \frac{a}{b})(a – \frac{a^2}{a+b}) $$
Solution
The given expression is equivalent to:
$$ ( \frac{1}{1} + \frac{a}{b})( \frac{a}{1} – \frac{a^2}{a+b}) $$
First, add and subtract the fractions in each of the expressions between the parentheses:
$$ (\frac{b+a}{b})( \frac{a^2 + ab -a^2}{a+b}) $$
Simplifying, we are left with:
$$ (\frac{b+a}{b})( \frac{ ab }{a+b}) $$
Now we multiply the fractions in the usual way, numerator by numerator and denominator by denominator:
$$ \frac{(b+a)ab}{b(a+b)} $$
After simplifying, i.e. canceling equal factors in the numerator and denominator, we are left with the final answer:
$$ a $$
EXAMPLE 7
Reduce the expressions in parentheses to algebraic fraction form, and then multiply them.
$$ (x – \frac{x}{y+1})( x + \frac{x}{y}) $$
Solution
Considering that $latex x = \frac{x}{1} $ we subtract the fractions in the first parenthesis and add them in the second one:
$$ (\frac{x(y+1) -x}{y+1})( \frac{xy + x}{y}) $$
Expanding the first numerator and take out the common factor x in the second numerator:
$$ (\frac{xy+x -x}{y+1})( \frac{x(y + 1)}{y}) $$
Simplifying:
$$ (\frac{xy}{y+1})( \frac{x(y + 1)}{y}) $$
We multiply the fractions in parentheses:
$$ \frac{x^2y(y+1)}{(y+1)y} $$
The common factors between the numerator and denominator are cancelled, leaving as final result:
$$ x^2 $$
EXAMPLE 8
Solve for the product of the three algebraic fractions shown below:
$$ \frac{5}{x} \cdot \frac{2x}{b^2} \cdot \frac{3b}{10} $$
Solution
We multiply the numerators and the denominators separately:
$$ \frac{30xb}{10xb^2} $$
After simplifying, we get the following:
$$ \frac{3}{b} $$
EXAMPLE 9
Solve the following:
$$ (1+\frac{x}{y})(1- \frac{x}{y}) $$
Solution
We have the product of an addition by a difference, which is equal to a difference of squares:
$$ 1^2-(\frac{x}{y})^2 $$
In the above expression, we have an algebraic fraction squared, which is equivalent to multiplying the fraction by itself:
$$ \frac{1}{1}-\frac{x^2}{y^2} $$
We solve the subtraction of algebraic fractions, and we are left with:
$$ \frac{y^2-x^2}{y^2} $$
Factor the numerator using the product of the difference of squares, to get the final result:
$$ \frac{(y-x)(x+y)}{y^2} $$
EXAMPLE 10
Multiply:
$$ (\frac{15x^3 + 15x^2}{20x^2-30x})(\frac{4x-6}{x+1}) $$
Solution
Before performing the multiplication, the common factor is taken out in the numerators and denominators:
$$ \frac{15x^2(x + 1)}{10x(2x-3)} \cdot \frac{2(2x-3)}{x+1} $$
Multiplying the fractions:
$$ \frac{30x^2(x + 1)(2x-3)}{10x(2x-3)(x+1)} $$
Canceling the common factors between the numerator and denominator, we have the final result:
$$ \frac{3x}{1} = 3x $$
Product of algebraic fractions – Practice problems


What is the result of multiplying the fractions and simplifying? $$\frac{5x^2}{x^2-2x} \cdot \frac{x^2-4}{x^2+2x} $$
Write the result in the input box.
See also
Interested in learning more about algebraic fractions? You can take a look at these pages: