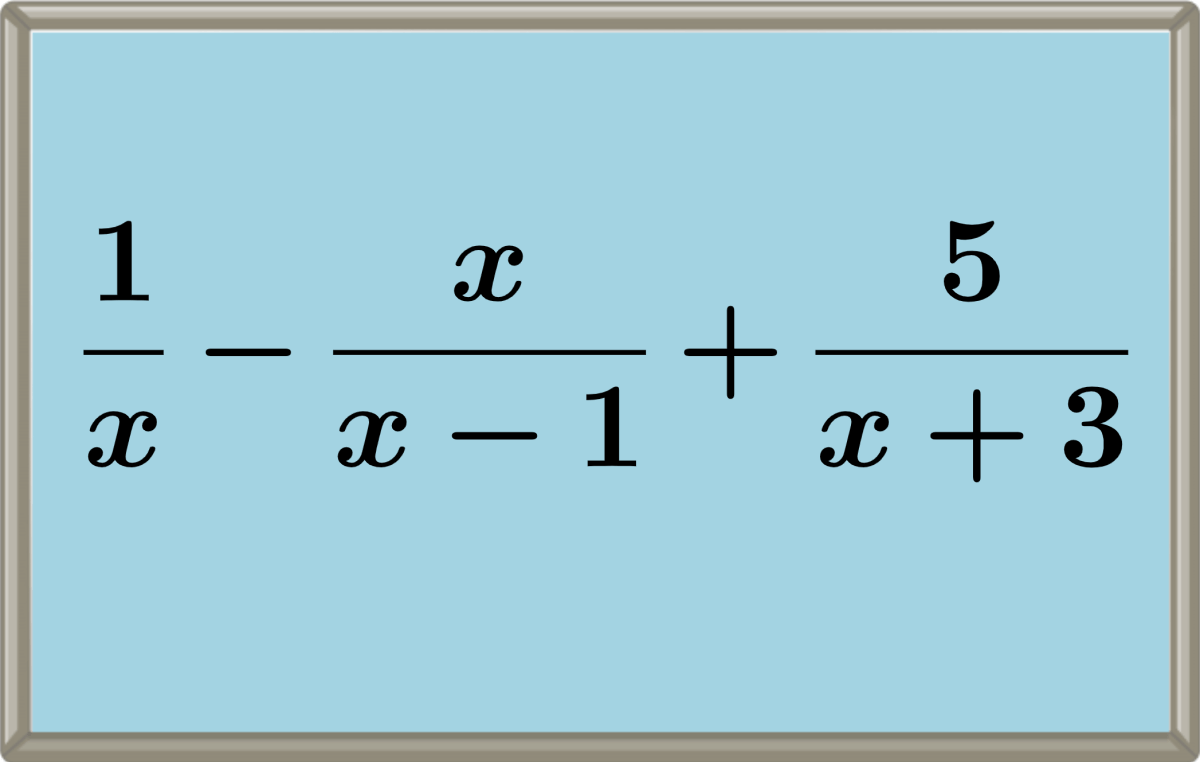The process to follow to add two or more algebraic fractions will depend on whether the fractions are like fractions or unlike. If the fractions are like, we have to start by calculating the lowest common denominator to rewrite them as equivalent like fractions.
Here, we will solve some exercises of addition of algebraic fractions. Then, we will look at some practice problems to apply what we have learned.
Examples with answers of adding algebraic fractions.
You can make a revision of how to add algebraic fractions in this article.
EXAMPLE 1
Add the following algebraic fractions:
$$\frac {x-1}{3}+\frac{1-8x}{3}$$
Solution
When the algebraic fractions to be added have the same denominator, whether it is a number or an algebraic expression, adding them is very easy, since it will be enough to write the same denominator and add the numerators.
In this case, the denominator of both algebraic expressions is 3, so we have:
$$\frac {x-1}{3}+\frac{1-8x}{3}=\frac{(x-1)+(1-8x)}{3}$$
Next, reduce the like terms in the numerator:
$$\frac {x-1}{3}+\frac{1-8x}{3}=\frac{(x-1)+(1-8x)}{3}$$
$$=\frac{(x-8x)+(-1+1)}{3}$$
$$=-\frac{7x}{3}$$
Therefore:
$$\frac {x-1}{3}+\frac{1-8x}{3}=-\frac{7x}{3}$$
EXAMPLE 2
Find the addition of these algebraic fractions:
$$\frac {4x^2-3}{x}+\frac{2x^2-1}{x}$$
Solution
The denominators of both fractions are the same, therefore:
$$\frac {4x^2-3}{x}+\frac{2x^2-1}{x} =\frac {(4x^2-3)+(2x^2-1)}{x}$$
Combining like terms, we have:
$$\frac {(4x^2-3)+(2x^2-1)}{x}=\frac {(4x^2+2x^2)+(-3-1)}{x}$$
$$=\frac {6x^2-4}{x}$$
The result is:
$$\frac {4x^2-3}{x}+\frac{2x^2-1}{x}=\frac {6x^2-4}{x}$$
EXAMPLE 3
Do the following addition and simplify the result as much as possible:
$$\frac {y}{y-6}+\frac{6+4y-y^2}{y-6}$$
Solution
In the case of summands with the same denominator, proceed as in the previous examples:
$$\frac {y}{y-6}+\frac{6+4y-y^2}{y-6}=\frac {y+6+4y-y^2}{y-6}$$
Next, the like terms in the numerator are added together:
$$\frac {y+6+4y-y^2}{y-6}=\frac {6+5y-y^2}{y-6}$$
$$=\frac {-y^2+5y+6}{y-6}$$
Now, if in the numerator we take out the common factor $latex (-1)$, we have a trinomial that can be factored:
$$=\frac {-y^2+5y+6}{y-6}= \frac {(-1)\cdot (y^2-5y-6)}{y-6} $$
Then, we have:
$$y^2-5y-6 = (y-6)\cdot(y+1) $$
Substituting in the addition and simplifying:
$$\frac {(-1)\cdot(y^2-5y-6)}{y-6} =\frac { (-1)\cdot(y-6)(y+1)}{y-6}$$
$$=-y-1$$
Therefore:
$$\frac {y}{y-6}+\frac{6+4y-y^2}{y-6}=-y-1$$
EXAMPLE 4
Find the result of the following:
$$\frac {x+3}{2}+\frac{5x+1}{7}$$
Solution
This is an example of addition of algebraic fractions with different denominators, so first, we determine the least common multiple (LCM) of the denominators.
Given that the denominators 2 and 7 are prime numbers, the least common multiple of both is the product of the values:
$latex lcm(2,7) = 2\times 7 = 14$
Therefore, the denominator of the addition will be 14. To find the numerator, divide the LCM by the denominator of the first fraction and multiply the result by the corresponding numerator.
This process is repeated for the second fraction, and the results are added together:
$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{7(x+3)+2(5x+1)}{14}$$
Then, the distributive property is applied to the numerator, and the like terms are added:
$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{7(x+3)+2(5x+1)}{14}$$
$$=\frac{7x+21+10x+2)}{14}$$
$$=\frac{17x+23}{14}$$
The result is:
$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{17x+23}{14}$$
EXAMPLE 5
Determine the addition of these algebraic fractions:
$$\frac{3}{2x}+\frac{4}{x^2}+\frac{5}{6x^3}$$
Solution
It is an addition of algebraic fractions with different denominators, therefore, we need to find the LCM of three algebraic expressions.
It is not difficult to realize that this algebraic expression is $latex 6x^3$, therefore:
$latex lcm[2x; x^2; 6x^3]=6x^3$
Dividing the LCM by each of the denominators of the addends, we see that the division is exact:
- $latex 6x^3\div 2x = 3x^2$
- $latex 6x^3\div x^2 = 6x$
- $latex 6x^3\div 6x^3 = 1$
The denominator of the addition will be the LCM, while the numerator is the sum of the products between the respective numerators and each of the results obtained:
$$\frac{3}{2x}+\frac{4}{x^2}+\frac{5}{6x^3}=\frac{3\cdot 3x^2+4\cdot 6x +5\cdot 1}{6x^3}$$
$$=\frac{9x^2+24x +5}{6x^3}$$
The numerator is irreducible, so we conclude that:
$$\frac{3}{2x}+\frac{4}{x^2}+\frac{5}{6x^3}=\frac{9x^2+24x +5}{6x^3}$$
EXAMPLE 6
Perform the following addition, simplifying the result as much as possible:
$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}$$
Solution
Note that $latex y^2-9$ is a difference of squares, and as such, can be factored as follows:
$latex y^2-9 = (y+3)(y-3)$
The addition can be written in this way, which is equivalent:
$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{(y+3)(y-3)}$$
The three denominators are different, therefore, we need to find their least common multiple:
$$lcm[(y-3);(y+3);(y+3)(y-3)]=(y+3)(y-3)$$
The denominator of the resulting fraction is the LCM of the denominators of the three fractions.
As for the numerator, divide the LCM by each of the denominators and multiply by the respective numerator, then add it all up, as in the previous example:
$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {(y+3)2y+(y-3)3y+10y}{(y+3)(y-3)}$$
The next step is to apply the distributive property in the numerator to expand it:
$$\frac {(y+3)2y+(y-3)3y+10y}{(y+3)(y-3)}=\frac {2y^2+6y+3y^2-9y+10y}{(y+3)(y-3)}$$
$$=\frac {5y^2+7y}{(y+3)(y-3)}$$
The expression obtained is irreducible, since between the numerator and the denominator there are no common factors, however, the numerator can be factored to obtain the following:
$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {y(5y+7)}{(y+3)(y-3)}$$
EXAMPLE 7
Carry out the addition proposed below:
$$\frac{10}{x}+\frac{2x}{x-3}$$
Solution
Since the denominators are different and have no factors in common, the LCM is simply their product:
$latex lcm[x; (x-3)]=x(x-3)$
Therefore, we have the following:
$$\frac{10}{x}+\frac{2x}{x-3}=\frac{10(x-3)+2x\cdot x}{x(x-3)}$$
$$=\frac{2x^2+10x-30}{x(x-3)}$$
The numerator can be factored as follows:
$$\frac{2x^2+10x-30}{x(x-3)}=\frac{2(x^2+5x-15)}{x(x-3)}$$
Then:
$$\frac{10}{x}+\frac{2x}{x-3}=\frac{2(x^2+5x-15)}{x(x-3)}$$
EXAMPLE 8
Add the following algebraic fractions:
$$\frac{9}{z-2}+\frac{3z}{2-z}$$
Solution
At first glance, it seems that the denominators of both fractions are different, however, multiplying the numerator and denominator of the second fraction by $latex (-1)$, the denominators become equal, and we have:
$$\frac{9}{z-2}+\frac{3z}{2-z}=\frac{9}{z-2}+\frac{(-1)\cdot(3z)}{(-1)\cdot(2-z)}$$
$$=\frac{9}{z-2}+\frac{(-3z)}{(z-2)}$$
$$=\frac{9-3z}{z-2}$$
$$=\frac{3(3-z)}{z-2}$$
The operation can be written as:
$$\frac{9}{z-2}+\frac{3z}{2-z}=\frac{3(3-z)}{z-2}$$
EXAMPLE 9
Perform the addition:
$$5y^2+\frac{9y}{y-6}$$
Solution
The first summand is not a fraction, but it can be written as such by putting a $latex 1$ in the denominator:
$$5y^2+\frac{9y}{y-6}=\frac {5y^2}{1}+\frac{9y}{y-6}$$
Then we calculate the $latex LCM$ of the denominators:
$latex lcm(1; y-6)= y-6$
Therefore:
$$5y^2+\frac{9y}{y-6}=\frac {5y^2}{1}+\frac{9y}{y-6}$$
$$=\frac {5y^2(y-6)+9y}{y-6}$$
$$=\frac {5y^3-30y^2+9y}{y-6}$$
$$=\frac {y(5y^2-30y+9)}{y-6}$$
EXAMPLE 10
Add the following algebraic fractions:
$$ \frac{x}{x^2+2x-8}+\frac{x+1}{x^2-3x+2}$$
Solution
First, if possible, the denominators are factored:
$$x^2+2x-8 =(x+4)\cdot(x-2)$$
$$x^2-3x+2 =(x-2)\cdot(x-1)$$
And the expression is rewritten:
$$\frac{x}{x^2+2x-8}+\frac{x+1}{x^2-3x+2}=\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}$$
Thus, the least common multiple of the denominators is:
$$lcm[(x+4)(x-2);(x-2)(x-1)] =(x-2)(x+4)(x-1)$$
Therefore:
$$\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}=\frac{x(x-1)+(x+1)(x+4)}{(x-2)(x+4)(x-1)}$$
Now the products that appear in the numerator are expanded:
$latex x(x-1)=x^2-x$
$latex (x+1)(x+4)=x^2+5x+4$
And they are added together, reducing like terms:
$$(x^2-x)+(x^2+5x+4) = 2x^2+4x+4= 2(x^2+2x+2)$$$
This result is substituted into the numerator:
$$\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}=\frac{x(x-1)+(x+1)(x+4)}{(x-2)(x+4)(x-1)}$$
$$=\frac{2(x^2+2x+2)}{(x-2)(x+4)(x-1)}$$
The result is:
$$ \frac{x}{x^2+2x-8}+\frac{x+1}{x^2-3x+2}=\frac{2(x^2+2x+2)}{(x-2)(x+4)(x-1)}$$
Adding algebraic fractions – Practice problems
What is the numerator of the fraction resulting from adding the fractions? $$\frac{2x}{x^2+3x+2} +\frac{3}{x+1} $$
Write the numerator in the input box.
See also
Interested in learning more about operations with algebraic fractions? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
