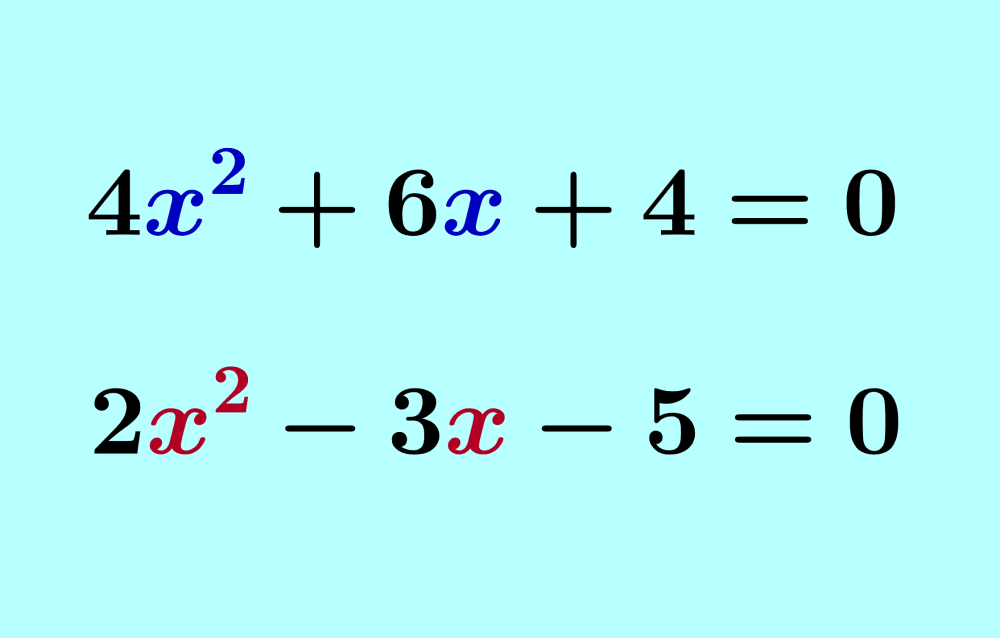A quadratic equation is an algebraic equation that has the form ax²+bx+c=0. We can use various methods to solve quadratic equations. Depending on the type of equation we have, some methods will be easier than others. Some of the more important methods include completing the square, using factoring, or using the quadratic formula.
Here, we will learn various methods to solve quadratic equations step-by-step. Then we will apply these methods to solve some practice problems.
- Steps to solve incomplete quadratic equations
- Steps to solve quadratic equations by factoring
- Steps to solve quadratic equations by completing the square
- Steps to solve quadratic equations with the quadratic formula
- Quadratic equations – Examples with answers
- Quadratic equations – Practice problems
- See also
Steps to solve incomplete quadratic equations
Incomplete quadratic equations are equations that have a missing term in the form $latex ax^2+bx+c$. Depending on the missing term, we have two types of incomplete quadratic equations.
Solving quadratic equations that do not have the term bx
Quadratic equations that do not have the bx term have the form $latex ax^2+c=0$. To solve these equations, we follow these steps:
Step 1: Simplify the equation if possible.
Step 2: Write the equation as follows:
$latex ax^2=-c$
Step 3: Isolate x² completely. For this, we divide the equation by a. Sometimes, the value of a is 1, so we don’t have to apply this step.
$latex x^2=-\frac{c}{a}$
Step 4: We take the square root of both sides:
$latex x=\pm\sqrt{-\frac{c}{a}}$
Note: Both positive and negative solutions must be considered because $latex (-a)^2=a^2$.
Solving quadratic equations that do not have the term c
Incomplete quadratic equations that do not have the c term have the form $latex ax^2+bx=0$. To solve these equations, we can follow the following steps:
Step 1: Simplify the equation if possible.
Step 2: Factor the x on the left-hand side of the equation:
$latex x(ax+b)=0$
Step 3: Form an equation with each factor:
$latex x=0~~$ and $latex ~~ax+b=0$
Step 4: Solve the equations:
$latex x=0~~$ or $latex ~~x=-\frac{b}{a}$
Note: One of the solutions will always be $latex x=0$.
Steps to solve quadratic equations by factoring
Factoring a quadratic equation consists of finding two factors of the equation to write it in the form $latex (x+p)(x+q)=0$. In this way, we can easily identify the roots of the quadratic equation.
To solve quadratic equations by factoring, we have to follow these steps:
Step 1: Simplify if possible and write the equation in the form $latex ax^2+bx+c=0$.
Step 2: Use any method to factor the quadratic equation and write it in the form $latex (x+p)(x+q)=0$.
Step 3: Obtain an equation with each factor by setting it equal to zero. For example $latex x+p=0$.
Step 4: Solve both linear equations.
Remember that to factor a quadratic equation, we have to transform the equation from the form $latex x^2+bx+c=0$ to the form $latex (x+p)(x+q)=0$. To achieve this, we have to find two factors, which when multiplied, result in the original quadratic equation.
For example, the equation $latex x^2+2x-3=0$ can be factored in the form $latex (x+3)(x-2)=0$, since multiplying the factors gives us the original equation.
You can review the methods of factoring quadratic equations by visiting our article: Factoring Quadratic Equations.
Steps to solve quadratic equations by completing the square
Completing the square is a factorization technique that involves transforming a quadratic equation from the form $latex ax^2+bx+c=0$ to the form $latex (x-h)^2+k=0$. This technique allows us to solve equations that cannot be easily factored.
Step 1: Simplify and write the equation in the form $latex ax^2+bx+c=0$.
Step 2: If the coefficient a is different from 1, we divide the entire equation by a to make the coefficient of the quadratic term equal to 1:
$latex x^2+bx+c=0$
Step 3: Divide the coefficient b by 2:
$$\left(\frac{b}{2}\right)$$
Step 4: Square the expression from step 3:
$$\left(\frac{b}{2}\right)^2$$
Step 5: Add and subtract the expression obtained in step 4 to the equation obtained in step 2:
$$x^2+bx+\left(\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Step 6: Factor the equation using the identity $latex x^2+2xy+y^2=(x+y)^2$:
$$\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Step 7: Simplify to get an equation of the following form:
$latex (x-h)^2+k=0$
Step 8: Rearrange the equation as follows:
$latex (x-h)^2=-k$
Step 9: Take the square root of both sides of the equation:
$latex x-h=\sqrt{-k}$
Step 10: Solve for x:
$latex x=h\pm \sqrt{-k}$
Steps to solve quadratic equations with the quadratic formula
The quadratic formula allows us to find both solutions of any quadratic equation. We can use this method when it is not possible to solve quadratic equations by any other method.
To solve quadratic equations using the general quadratic formula, we can follow the steps below:
Step 1: Simplify and write the equation in the form $latex a{{x}^2}+bx+c=0$.
Step 2: Substitute the coefficients a, b, and c into the quadratic formula:
| $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$ |
Step 3: Use the ± sign. The result of the square root must be added and subtracted separately to obtain both solutions to the equation.
A quadratic equation can have two real roots, one repeated real root, or no real roots. This depends on the discriminant of the equation, which is the value that goes inside the square root sign, that is, $latex b^2-4ac$.
Therefore, depending on the value of the discriminant, we have the following:
- When $latex b^2-4ac>0$, the equation has two real roots.
- When $latex b^2-4ac<0$, the equation has no real roots.
- When $latex b^2-4ac=0$, the equation has a repeated root.
If the value inside the square root is positive, we will have two real roots. If that value is negative, we will not have real roots (but we will have imaginary or complex roots). If that value is equal to zero, we have a single root.
To learn how to derive the general quadratic formula, you can visit our General Quadratic Formula – Steps to Quadratic Formula.
Quadratic equations – Examples with answers
The following examples are solved using the methods seen above. Each example has its respective solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Find the solutions to the equation $latex x^2-36=0$.
Solution
This equation is an incomplete quadratic equation that does not have the bx term. Therefore, we can solve it by isolating for the x² term and taking the square root of both sides:
$latex x^2-36=0$
$latex x^2=36$
$latex x=\pm\sqrt{36}$
$latex x=\pm 6$
The solutions of the equation are $latex x=6$ and $latex x=-6$.
EXAMPLE 2
Find the solutions to the equation $latex 2x^2-9x=0$.
Solution
This equation is an incomplete quadratic equation that does not have the c term. We can solve it by factoring the x and forming an equation with each factor:
$latex 2x^2-9x=0$
$latex x(2x-9)=0$
$latex x=0~~ $ or $latex ~~2x-9=0$
$latex x=0 ~~$ or $latex ~~x=\frac{9}{2}$
The solutions of the equation are $latex x=0$ and $latex x=\frac{9}{2}$.
EXAMPLE 3
Apply the factoring method to solve the equation $latex x^2+2x-15=0$.
Solution
We can factor the equation as follows:
$latex x^2+2x-15=0$
$latex (x+5)(x-3)=0$
Forming an equation with each factor and solving, we have:
$latex x+5=0~~$ or $latex ~~x-3=0$
$latex x=-5~~$ or $latex ~~x=3$
The solutions of the equation are $latex x=-5$ and $latex x=3$.
EXAMPLE 4
Find the solutions to the equation $latex 2x^2-3x-20=0$ using the factoring method.
Solution
Factoring the left-hand side of the equation, we have:
$latex 2x^2-3x-20=0$
$latex (2x+5)(x-4)=0$
Forming an equation with each factor and solving, we have:
$latex 2x+5=0~~$ or $latex ~~x-4=0$
$latex x=-\frac{5}{2}~~$ or $latex ~~x=4$
The solutions to the equation are $latex x=-\frac{5}{2}$ and $latex x=4$.
EXAMPLE 5
Solve the equation $latex x^2-3x+1=0$ using the method of completing the square.
Solution
The coefficient b of this quadratic equation is -3. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-3}{2}\right)^2$$
Adding and subtracting this expression to the original quadratic equation, we have:
$$x^2-3x+1=x^2-2x+\left(\frac{-3}{2}\right)^2-\left(\frac{-3}{2}\right)^2+1$$
Now, we can complete the square and simplify:
$latex = (x-\frac{3}{2})^2-\left(\frac{-3}{2}\right)^2+1$
$latex = (x-\frac{3}{2})^2-\frac{5}{4}$
We rearrange the equation as follows:
$latex ⇒ (x-\frac{3}{2})^2=\frac{5}{4}$
Taking the square root of both sides, we have:
⇒ $latex x-\frac{3}{2}=\sqrt{\frac{5}{4}}$
⇒ $latex x-\frac{3}{2}=\frac{\sqrt{5}}{2}$
Solving, we have:
⇒ $latex x=\frac{3}{2}\pm \frac{\sqrt{5}}{2}$
EXAMPLE 6
Solve the equation $latex 2x^2+8x-10=0$ using the method of completing the square.
Solution
In this case, we have to start by dividing the entire equation by 2 to make the coefficient of the quadratic term equal to 1:
⇒ $latex x^2+4x-5=0$
The coefficient b of the simplified quadratic equation is equal to 4. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Now, let’s add and subtract that value from the equation to get:
$$x^2+4x-5=x^2+4x+2^2-2^2-5$$
When we complete the square and simplify, we have:
$latex = (x+2)^2-4-5$
$latex = (x+2)^2-9$
Now, we rearrange the equation as follows:
⇒ $latex (x+2)^2=9$
And we take the square root of both sides:
⇒ $latex x+2=3~~$ or $latex ~~x+2=-3$
Solving, we have:
⇒ $latex x=1~~$ or $latex ~~x=-5$
EXAMPLE 7
Find the solutions to the equation $latex 3x^2+x-3=0$ using the quadratic formula. Use two decimal places.
Solution
We can identify the values $latex a=3$, $latex b=1$, and $latex c=-3$. Therefore, substituting those values into the general formula, we have:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(1)\pm \sqrt{( 1)^2-4(3)(-3)}}{2(3)}$$
$$=\frac{-1\pm \sqrt{1+36}}{6}$$
$$=\frac{-1\pm \sqrt{37}}{6}$$
$$x=-1.18\text{ or }0.85$$
The solutions of the equation are $latex x=-1.18$ and $latex x=0.85$.
Quadratic equations – Practice problems
Use the methods studied above to solve the following quadratic equations.
See also
Interested in learning more about quadratic equations? Take a look at these pages: