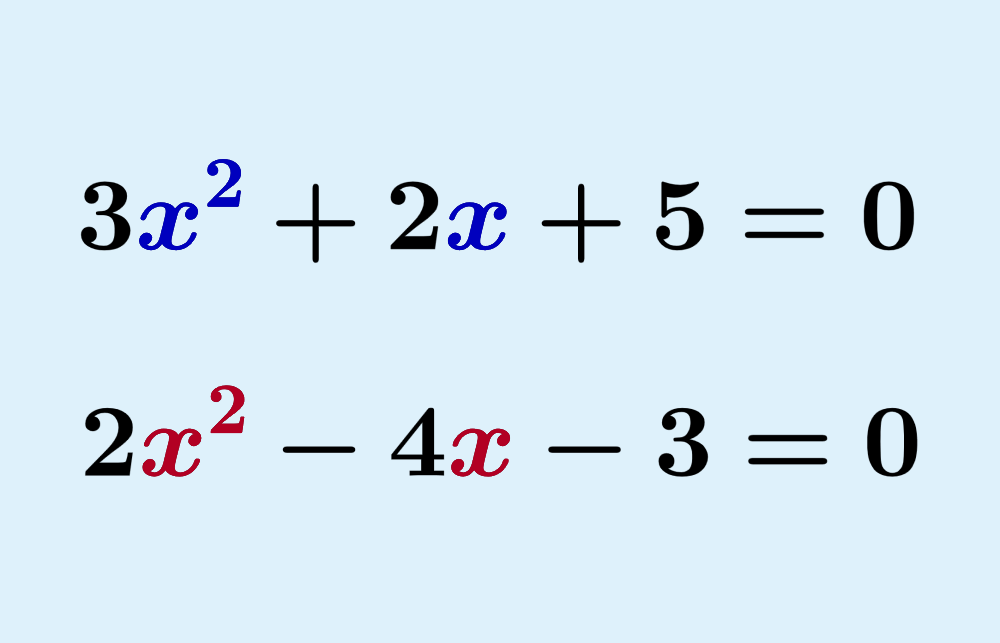Quadratic equations word problems are math problems in which the equations are not given directly. These problems can be solved by using the given information to obtain a quadratic equation of the form $latex ax^2+bx+c$. We can then use the factoring method, the completing the square method or the quadratic formula to solve the equation.
Here, we will look at 10 quadratic equations word problems with answers. In addition, you will also be able to practice with 5 word problems to solve.
10 quadratic equations word problems with answers
The following problems are solved by forming a quadratic equation with the given word problem. Try to solve the problems yourself before looking at the solution.
PROBLEM 1
If the sum of two numbers is equal to 17 and their product is equal to 60, what are the numbers?
Solution
We can use the letters X (smaller number) and Y (larger number) to represent both numbers. Then, from the statement, we can obtain the following equations:
$latex X+Y=17~~[1]$
$latex XY=60~~[2]$
Now, we can rearrange equation 1 to get $latex Y=17-X$. Substituting this expression into the second equation, we have:
$latex X(17-X)=60$
Expanding the parentheses and rearranging the equation, we have:
$latex 17X-X^2=60$
$latex X^2-17X+60=0$
Now, we can factor the equation to solve:
$latex X^2-17X+60=0$
$latex (X-12)(X-5)=0$
$latex X-12=0~~$ or $latex ~~X-5=0$
$latex X=12~~$ or $latex ~~X=5$
Therefore, we have:
- If $latex X=5$, we have $latex Y=17-5=12$. This solution is correct because X<Y.
- If $latex X=12$, we have $latex Y=17-12=5$
The numbers are 12 and 5.
PROBLEM 2
The difference between two numbers is equal to 5 and their product is equal to 126. What are these numbers?
Solution
Using the information in the statement and using the letters X (smaller number) and Y (larger number) to represent the numbers, we can obtain the following equations:
$latex Y-X=5 ~~[1]$
$latex XY=126~~[2]$
Now, we can write the first equation as $latex Y=5+X$ and substituting it into the second equation, we have:
$latex X(5+X)=126$
$latex 5X+X^2=126$
$latex X^2+5X-126=0$
Now, we can factor and solve:
$latex (X+13)(X-9)=0$
$latex X+13=0~~$ or $latex ~~X-9=0$
$latex X=-13~~$ or $latex ~~X=9$
Therefore, we have:
- If $latex X=-13$, we have $latex Y=5-13=-8$
- If $latex X=9$, we have $latex Y=5+9=14$. This solution is correct because $latex XY=126$
The numbers are 12 and 5.
PROBLEM 3
If the area of a rectangle is 78 square units and its longest side is 7 units longer than its shortest side, what are the lengths of the sides?
Solution
We can represent the shorter side with x. This means that the longest side is equal to x+7.
Also, we remember that the area of a rectangle is equal to the product of its sides. Therefore, we can form the following equation:
$latex x(x+7)=78$
Expanding and writing the equation in the form $late ax^2+bx+c=0$, we have:
$latex x^2+7x-78=0$
Now, we can use factorization to solve:
$latex (x+13)(x-6)=0$
$latex x+13=0~~$ or $latex ~~x-6=0$
$latex x=-13~~$ or $latex ~~x=6$
Since we can’t have negative lengths, we have $latex x=6$, so the lengths are 6 and 13.
PROBLEM 4
Find the lengths of the sides of a rectangle that has an area of 200 square units if the longer side is twice the length of the shorter side.
Solution
Using the letters X (short side) and Y (long side) to represent the sides, we can obtain the following equations using the given information:
$latex Y=2X~~[1]$
$latex XY=200~~[2]$
Now, we can substitute equation 1 into equation 2 and we have:
$latex X(2X)=200$
$latex 2X^2=200$
To solve this equation, we have to isolate X² completely and take the square root of both sides:
$latex X^2=100$
$latex X=\pm\sqrt{100}$
$latex X=\pm 10$
Since a length can’t be negative, we have $latex X=10$. Therefore, we have $latex Y=20$.
PROBLEM 5
The difference between the squares of two consecutive odd numbers is equal to 48. Find both numbers.
Solution
Representing the first number with x, we can deduce that a consecutive odd number is equal to $latex x+2$. Therefore, using the information in the statement, we form an equation with the squares of the consecutive numbers:
$latex (x+2)^2-x^2=48$
Expanding, simplifying and solving, we have:
$latex x^2+4x+4-x^2=48$
$latex 4x+4=48$
$latex 4x=44$
$latex x=11$
The consecutive odd numbers are 11 and 13.
PROBLEM 6
The sides of a right triangle have lengths x, x+2, and 10. If 10 is the hypotenuse of the triangle, find the value of x.
Solution
Since the triangle is a right triangle, we can use the Pythagorean theorem to find an equation for the lengths of the three sides of the triangle.
The statement tells us that 10 is the hypotenuse of the triangle. Therefore, we have:
$latex x^2+(x+2)^2=10^2$
Expanding and simplifying the equation, we have:
$latex x^2+(x+2)^2=10^2$
$latex x^2+x^2+4x+4=100$
$latex 2x^2+4x+4=100$
$latex 2x^2+4x-96=0$
Now, we can divide the entire equation by 2 to simplify it:
$latex x^2+2x-48=0$
Solving by factorization, we have:
$latex (x+8)(x-6)=0$
$latex x+8=0~~$ or $latex ~~x-6=0$
$latex x=-8~~$ or $latex ~~x=6$
Since we can’t have a negative length, the answer is $latex x=6$.
PROBLEM 7
If the product of two numbers is equal to 48 and their average is equal to 7, find both numbers.
Solution
We can represent one of the numbers with x. This means that the other number is equal to 48/x since their product is equal to 48.
Therefore, considering that the average of two numbers is equal to the sum of the numbers divided by 2, we have:
$latex \frac{x+48/x}{2}=7$
Simplifying, we have:
$latex x+\frac{48}{x}=14$
$latex x^2+48=14x$
$latex x^2-14x+48=0$
Now, we can solve by factorization:
$latex (x-8)(x-6)=0$
$latex x-8=0~~$ or $latex ~~x-6=0$
$latex x=8~~$ or $latex ~~x=6$
The numbers are 6 and 8.
PROBLEM 8
If the side length of a square is increased by 4, its area is multiplied by 9. Find the side length of the original square.
Solution
In this problem, there are two areas that we need to consider, the area of the original square and the area of the larger square (length +4).
Using the x to represent the sides of the original square and remembering that the area of a square is equal to the length of one of the sides squared, we have:
Larger area = 9 × Original area
$latex (x+4)^2=9x^2$
Expanding and simplifying, we have:
$latex x^2+8x+16=9x^2$
$latex 8x^2-8x-16=0$
We can divide the entire equation by 8 and solving by factoring, we have:
$latex x^2-x-2=0$
$latex (x-2)(x+1)=0$
$latex x-2=0~~$ or $latex ~~x+1=0$
$latex x=2~~$ or $latex ~~x=-1$
Since a length cannot be negative, the answer is $latex x=2$.
PROBLEM 9
The shortest side of a right triangle is 4 units less than its hypotenuse. The difference between the short side and the intermediate side is 2 units. If the shorter side is x-2, find the value of x.
Solution
From the statement, we can deduce the following lengths of the triangle:
- Short side = x-2
- Intermediate side = x (2 units difference with short side)
- Hypotenuse = x+2 (4 units more than short side)
Now, we can use the Pythagorean theorem to write an equation for the three lengths:
$latex (x-2)^2+x^2=(x+2)^2$
Expanding and simplifying, we have:
$$x^2-4x+4+x^2=x^2+4x+4$$
$$x^2-4x+4+x^2-x^2-4x-4=0$$
$latex x^2-8x=0$
$latex x(x-8)=0$
$latex x=0~~$ or $latex ~~x=8$
Since the length cannot be 0, we have $latex x=8$.
PROBLEM 10
The figure below has an area of 100 square units. Find the value of x.
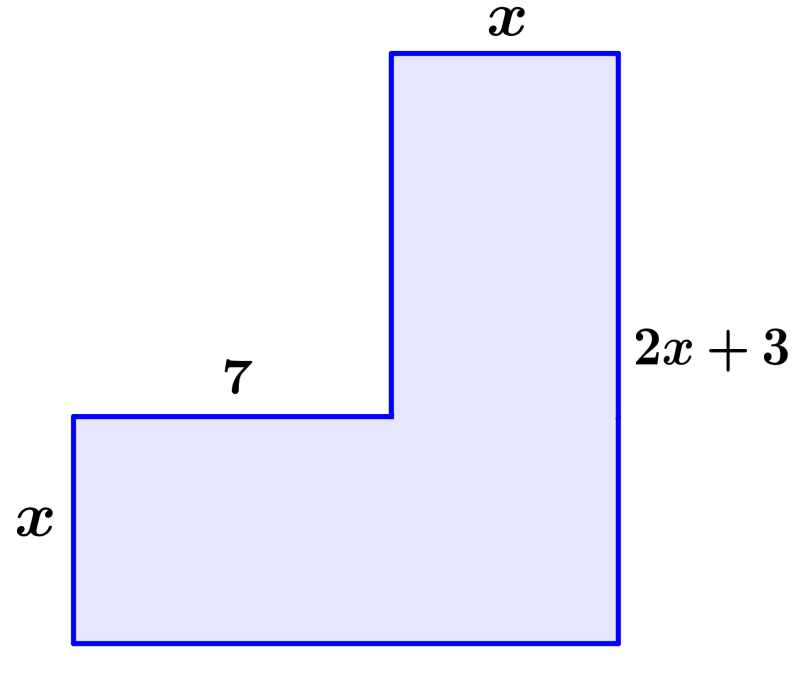
Solution
We can divide the figure into two rectangles, one rectangle has the area 7x and the other rectangle has the area x(2x+3). Adding these areas, we have:
$latex 7x+x(2x+3)=100$
Expanding and simplifying, we have:
$latex 7x+2x^2+3x=100$
$latex 2x^2+10x-100=0$
Now, we can divide the entire equation by 2 and solve by factoring:
$latex x^2+5x-50=0$
$latex (x+10)(x-5)=0$
$latex x=-10~~$ or $latex ~~x=5$
Since we can’t have a negative length, the answer is $latex x=5$.
Quadratic equations word problems to solve
Solve the following problems using any method of solving quadratic equations.
See also
Interested in learning more about quadratic equations? Take a look at these pages: