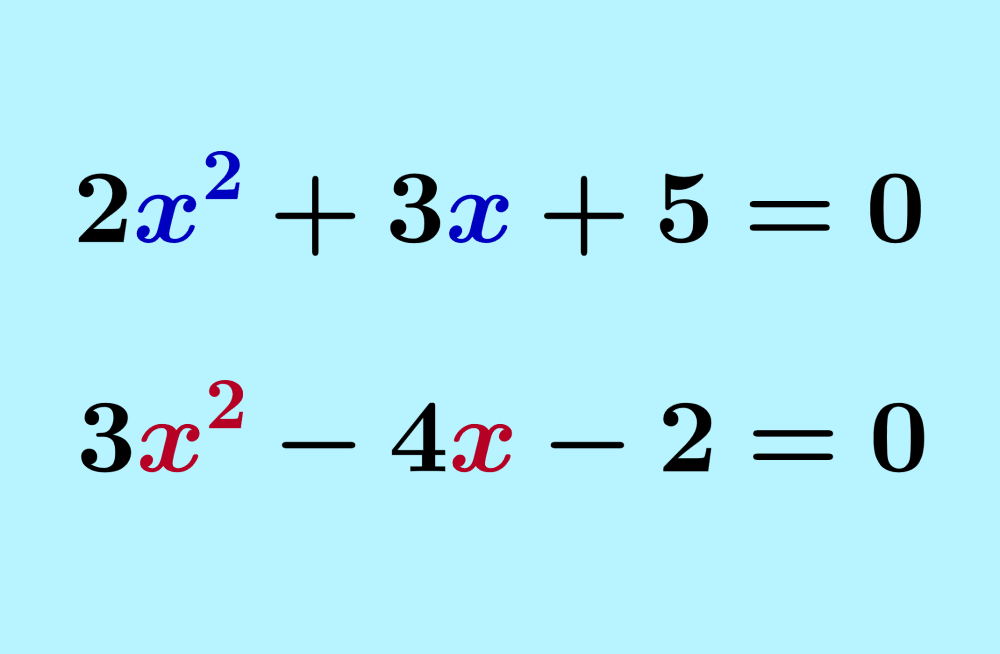20 Quadratic Equation Examples with Answers

This equation is an incomplete quadratic equation that does not have the bx term. We can solve this equation by isolating the x² term and taking the square root of both sides of the equation:

$latex x^2-25=0$

$latex x^2=25$

Taking the square root of both sides, we have:

$latex x=\pm \sqrt{25}$

$latex x=\pm 5$

The solutions to the equation are $latex x=5$ and $latex x=-5$.

This is an incomplete quadratic equation that does not have the c term. To solve this equation, we need to factor x and then form an equation with each factor:

$latex x^2-4x=0$

$latex x(x-4)=0$

Forming an equation with each factor, we have:

$latex x=0~~$ or $latex ~~x-4=0$

$latex x=0~~$ or $latex ~~x=4$

The solutions of the equation are $latex x=0$ and $latex x=4$.

We can solve this equation using the factoring method. For this, we look for two numbers that when multiplied are equal to 6 and when added are equal to 5.

The two numbers we are looking for are 2 and 3. Therefore, we have:

$latex x^2+5x+6=0$

$latex (x+2)(x+3)=0$

Now, we form an equation with each factor and solve:

$latex x+2=0~~$ or $latex ~~x+3=0$

$latex x=-2~~$ or $latex ~~x=-3$

The solutions to the equation are $latex x=-2$ and $latex x=-3$.

We can solve this equation by factoring. For this, we look for two numbers, which when multiplied are equal to -7 and when added are equal to -6.

The numbers we are looking for are -7 and 1. Therefore, we have:

$latex x^2-6x-7=0$

$latex (x-7)(x+1)=0$

Forming an equation with each factor, we have:

$latex x-7=0~~$ or $latex ~~x+1=0$

$latex x=7~~$ or $latex ~~x=-1$

The solutions to the equation are $latex x=7$ and $latex x=-1$.

This equation is an incomplete quadratic equation of the form $latex ax^2+c=0$. We can solve this equation by solving for x² and taking the square root of both sides:

$latex 2x^2-32=0$

$latex 2x^2=32$

$latex x^2=16$

Taking the square root of both sides, we have:

$latex x=\pm \sqrt{16}$

$latex x=\pm 4$

The solutions of the equation are $latex x=4$ and $latex x=-4$.

This equation is an incomplete quadratic equation of the form $latex ax^2+bx=0$. To solve this equation, we can factor 4x from both terms and then form an equation with each factor:

$latex 4x^2+8x=0$

$latex 4x(x+2)=0$

Forming an equation with each factor, we have:

$latex 4x=0~~$ or $latex ~~x+2=0$

$latex x=0~~$ or $latex ~~x=-2$

The solutions to the equation are $latex x=0$ and $latex x=-2$.

To complete the square, we take the coefficient b, divide it by 2, and square it. Then, we have:

$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$

$$=2^2$$

Now, we add and subtract that value to the quadratic equation:

$$x^2+4x-6=x^2+4x+2^2-2^2-6$$

Now, we can complete the square and simplify:

$latex = (x+2)^2-4-6$

$latex = (x+2)^2-10$

Thus, we have the equation:

$latex (x+2)^2=10$

Taking the square root of both sides, we have:

⇒ $latex x+2=\sqrt{10}$

Solving, we have:

⇒ $latex x=-2\pm \sqrt{10}$

We can identify the coefficients $latex a=1$, $latex b=-8$, and $latex c=4$. Using these values in the quadratic formula, we have:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$$x=\frac{-(-8)\pm \sqrt{( -8)^2-4(1)(4)}}{2(1)}$$

$$=\frac{8\pm \sqrt{64-16}}{2}$$

$$=\frac{8\pm \sqrt{48}}{2}$$

$$x=7.46 \text{ or } 0.54$$

The solutions are $latex x=7.46$ and $latex x=0.54$.

We can divide the entire equation by 2 to make the coefficient of the quadratic term equal to 1:

⇒ $latex x^2+4x-5=0$

Now, we take the coefficient b, divide it by 2 and square it. Therefore, we have:

$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$

$$=2^2$$

Adding and subtracting that value to the quadratic expression, we have:

$$x^2+4x-5=x^2+4x+2^2-2^2-5$$

Completing the square and simplifying, we have:

$latex = (x+2)^2-4-5$

$latex = (x+2)^2-9$

Now, we write the equation like this:

⇒ $latex (x+2)^2=9$

And we take the square root of both sides:

⇒ $latex x+2=\pm 3$

Solving, we have:

⇒ $latex x=1$ or $latex x=-5$

We can identify the coefficients $latex a=1$, $latex b=-10$, and $latex c=25$. Using them in the general quadratic formula, we have:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$$x=\frac{-(-10)\pm \sqrt{( -10)^2-4(1)(25)}}{2(1)}$$

$$=\frac{10\pm \sqrt{100-100}}{2}$$

$$=\frac{10\pm \sqrt{0}}{2}$$

$$=\frac{10}{2}$$

$latex x=5$

In this case, we have a single repeated root $latex x=5$.

First, we need to simplify this equation and write it in the form $latex ax^2+bx+c=0$:

$latex 4x^2+5=2x^2+20$

$latex 4x^2-2x^2+5-20=0$

$latex 2x^2-15=0$

Now, we can see that it is an incomplete quadratic equation that does not have the bx term. Therefore, we can solve it by solving for x² and taking the square root of both sides:

$latex 2x^2-15=0$

$latex 2x^2=15$

$latex x^2=\frac{15}{2}$

$latex x=\pm \sqrt{\frac{15}{2}}$

To solve the equation, we have to start by writing it in the form $latex ax^2+bx+c=0$. Therefore, we have:

$latex 5x^2+5x=2x^2+10x$

$latex 5x^2-2x^2+5x-10x=0$

$latex 3x^2-5x=0$

We see that it is an incomplete equation that does not have the term c. Thus, we can solve it by factoring x:

$latex 3x^2-5x=0$

$latex x(3x-5)=0$

$latex x=0~~$ or $latex ~~3x-5=0$

$latex x=0~~$ or $latex ~~x=\frac{5}{3}$

To use the general formula, we have to start by writing the equation in the form $latex ax^2+bx+c=0$:

$latex 3x^2+5x-4=x^2-2x$

$latex 2x^2+7x-4=0$

Now, we have the coefficients $latex a=2$, $latex b=7$, and $latex c=-4$. Therefore, using these values in the quadratic formula, we have:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$$x=\frac{-(7)\pm \sqrt{( 7)^2-4(2)(-4)}}{2(2)}$$

$$=\frac{-7\pm \sqrt{49+32}}{4}$$

$$=\frac{-7\pm \sqrt{81}}{2}$$

$$=\frac{-7\pm 9}{2}$$

$$=-8 \text{ or }1$$

The solutions of the equation are $latex x=-8$ and $latex x=1$.

To solve this equation, we need to expand the parentheses and simplify to the form $latex ax^2+bx+c=0$. Therefore, we have:

$$(3x+1)(2x-1)-(x+2)^2=5$$

$$6x^2-x-1-(x^2+4x+4)=5$$

$latex 5x^2-5x-5=5$

$latex 5x^2-5x-10=0$

Now, we can solve by factorization:

$latex 5x^2-5x-10=0$

$latex 5(x^2-x-2)=0$

$latex 5(x+1)(x-2)=0$

$latex x+1=0~~$ or $latex ~~x-2=0$

$latex x=-1~~$ or $latex ~~x=2$

We have to start by writing the equation in the form $latex ax^2+bx+c=0$:

$latex -x^2+3x+1=-2x^2+6x$

$latex x^2-3x+1=0$

Now, we see that the coefficient b in this equation is equal to -3. Therefore, we have:

$$\left(\frac{b}{2}\right)^2=\left(\frac{-3}{2}\right)^2$$

Adding and subtracting this value to the quadratic equation, we have:

$$x^2-3x+1=x^2-2x+\left(\frac{-3}{2}\right)^2-\left(\frac{-3}{2}\right)^2+1$$

Completing the square and simplifying, we have:

$latex = (x-\frac{3}{2})^2-\left(\frac{-3}{2}\right)^2+1$

$latex = (x-\frac{3}{2})^2-\frac{5}{4}$

Now, we write the equation as follows:

$latex ⇒ (x-\frac{3}{2})^2=\frac{5}{4}$

Taking the square root of both sides, we have:

⇒ $latex x-\frac{3}{2}=\sqrt{\frac{5}{4}}$

⇒ $latex x-\frac{3}{2}=\frac{\sqrt{5}}{2}$

Solving, we have:

⇒ $latex x=\frac{3}{2}\pm \frac{\sqrt{5}}{2}$

We can use the values $latex a=5$, $latex b=4$, and $latex c=10$ in the quadratic formula:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$$x=\frac{-(4)\pm \sqrt{( 4)^2-4(5)(10)}}{2(5)}$$

$$=\frac{-5\pm \sqrt{16-200}}{10}$$

$$=\frac{-5\pm \sqrt{-184}}{10}$$

We can see that we got a negative number inside the square root. $latex \sqrt{-184}$ is not a real number, so the equation has no real roots.

This equation does not appear to be quadratic at first glance. However, we can multiply it by $latex x(x-1)$ to eliminate the fractions, and we have:

$$\frac{4}{x-1}+\frac{3}{x}=3$$

$$4x+3(x-1)=3x(x-1)$$

$$4x+3x-3=3x^2-3x$$

$latex 3x^2-10x+3=0$

Now, we can factor this equation to solve it:

$latex 3x^2-10x+3=0$

$latex (3x-1)(x-3)=0$

$latex 3x-1=0~~$ or $latex ~~x-3=0$

$latex x=\frac{1}{3}~~$ or $latex ~~x=3$

To simplify fractions, we can cross multiply to get:

$$ (2x+1)(x+7)=(3x-1)(x+5)$$

Expanding and simplifying, we have:

$$ 2x^2+15x+7=3x^2+14x-5 $$

$latex x^2-x-12=0$

Factoring and solving, we have:

$latex (x+3)(x-4)=0$

$latex x+3=0~~$ or $latex ~~x-4=0$

$latex x=-3~~$ or $latex ~~x=4$

To solve this problem, we can form equations using the information in the statement. We use the letters X (smaller number) and Y (larger number) to represent the numbers:

$latex X+Y=17~~[1]$

$latex XY=60~~[2]$

Writing equation 1 as $latex Y=17-X$ and substituting it into the second equation, we have:

$latex X(17-X)=60$

We can expand and write it in the form $latex ax^2+bx+c=0$:

$latex 17X-X^2=60$

$latex X^2-17X+60=0$

Now, we can solve the equation by factoring:

$latex X^2-17X+60=0$

$latex (X-12)(X-5)=0$

$latex X-12=0~~$ or $latex ~~X-5=0$

$latex X=12~~$ or $latex ~~X=5$

Therefore, we have:

• If $latex X=5$, we have $latex Y=17-5=12$. This solution is the correct one because X<Y.
• If $latex X=12$, we have $latex Y=17-12=5$

The numbers are 12 and 5.

To solve this problem, we have to use the given information to form equations. Let’s represent the shorter side with x. This means that the longest side is equal to x+7.

Now considering that the area of a rectangle is found by multiplying the lengths of its sides, we have:

$latex x(x+7)=78$

Expanding and writing the equation in the form $latex ax^2+bx+c=0$, we have:

$latex x^2+7x-78=0$

Solving by factorization, we have:

$latex (x+13)(x-6)=0$

$latex x+13=0~~$ or $latex ~~x-6=0$

$latex x=-13~~$ or $latex ~~x=6$

Since we can’t have negative lengths, we have $latex x=6$, so the lengths are 6 and 13.