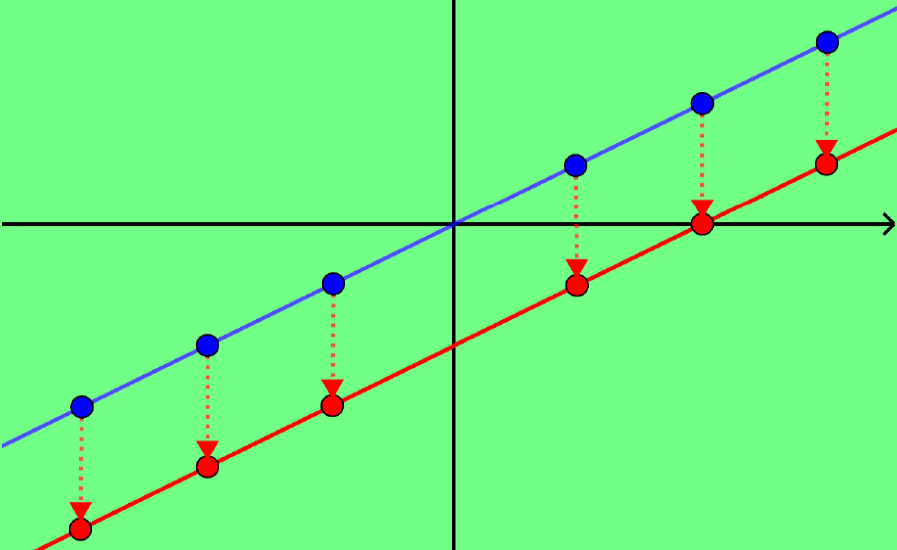
To determine whether a function is linear or not, we need to verify that the equation is a polynomial of the first degree. This means that the function must have the form $latex f(x)=mx+b$ when reorganized, and the independent variable x must have an exponent of 1. We will learn more about this with some exercises.
What are linear functions?
A linear function is an algebraic equation, in which each term is either a constant or the product of a constant and a variable (raised to the first power). For example, the equation $latex y=ax+b$ is a linear function since both variables x and y meet the criteria, and both constants a and b do as well.
The exponent of x is 1, that is, it is raised to the first power and the equation follows the definition of a function: for each input (x) there is only one output (y). The graph of a linear function is a straight line.
EXAMPLES
The following are linear functions:
- $latex f(x)=4x+3$
- $latex y=2x-5$
- $latex x+2y=4$
- $latex f(x)=\frac{1}{3}x+6$
Graphs of linear functions
The origin of the name “linear” comes from the fact that the set of solutions of this type of function forms a straight line in the Cartesian plane.
On the graph of a linear function $latex f(x)=mx+b$, m determines the slope of that line, that is, the steepness, and b determines the y-intercept, that is, the point where the line crosses the y-axis.
If you need help with this topic, check out our guide on how to graph linear functions.
EXAMPLES
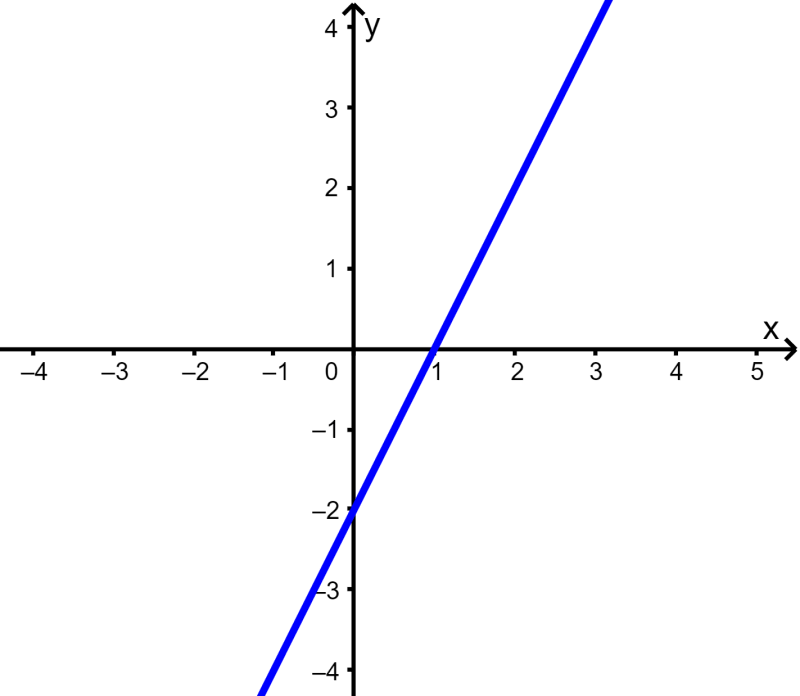
The following is the graph of $latex f(x)=2x-2$:
The following is the graph of $latex y=-x+3$:
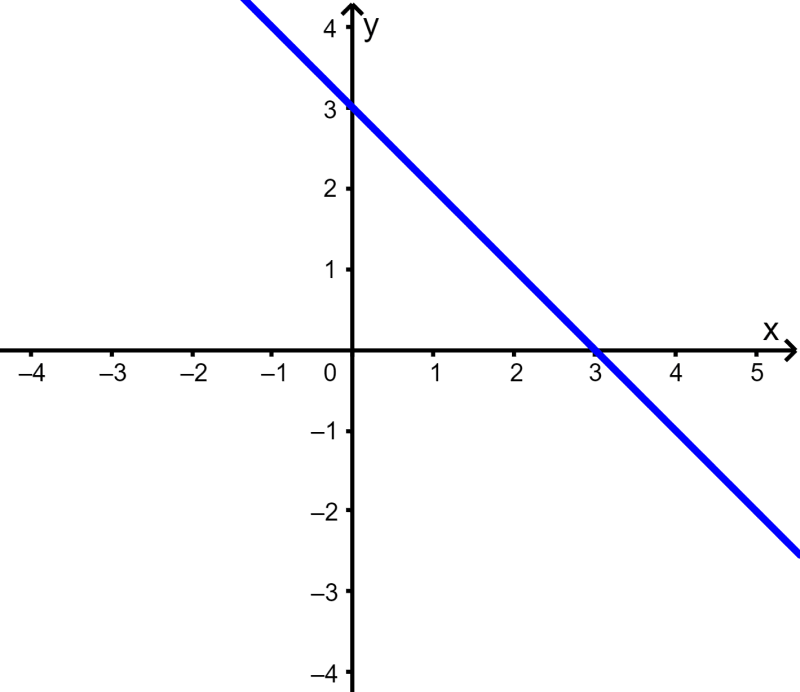
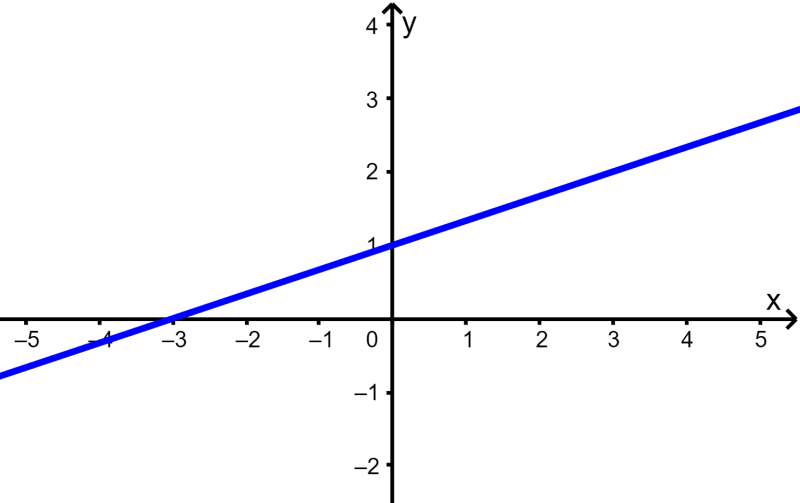
The following is the graph of $latex f(x)=\frac{1}{3}x+1$:
How to know if a function is linear?
A linear function creates a straight line when graphed on the Cartesian plane. Therefore, if it is possible to graph the function, you can easily determine if a function is linear by checking that its graph produces a straight line.
To know if a function is linear without having to graph it, we need to check if the function has the characteristics of a linear function. Linear functions are polynomials of the first degree.
Verify that the dependent variable or y is by itself on one side of the equation. If it is not, rearrange the equation to isolate the dependent variable. For example, if we have the equation $latex 3x+4y=4$, we move the $latex 3x$ to the right to get $latex 4y=-3x+4$ and then divide the entire equation by 4 to get $latex y=-\frac{3}{4}x+1$.
Now, we have to verify that the equation formed is indeed a linear function. For an equation to be a linear function, the equation must be a polynomial of the first degree. This means that the power of the independent variable or x must be 1. In our example, we see that x has a power of 1, thus, $latex y = -\frac{3}{4} x + 1$ is a linear function.
Examples to determine if a function is linear
EXAMPLE 1
Determine whether the equation $latex y=3x+2$ is a linear function.
Solution: We can easily see that the variable x has a power of 1, therefore, the equation represents a linear function. We can verify this by plotting its graph:
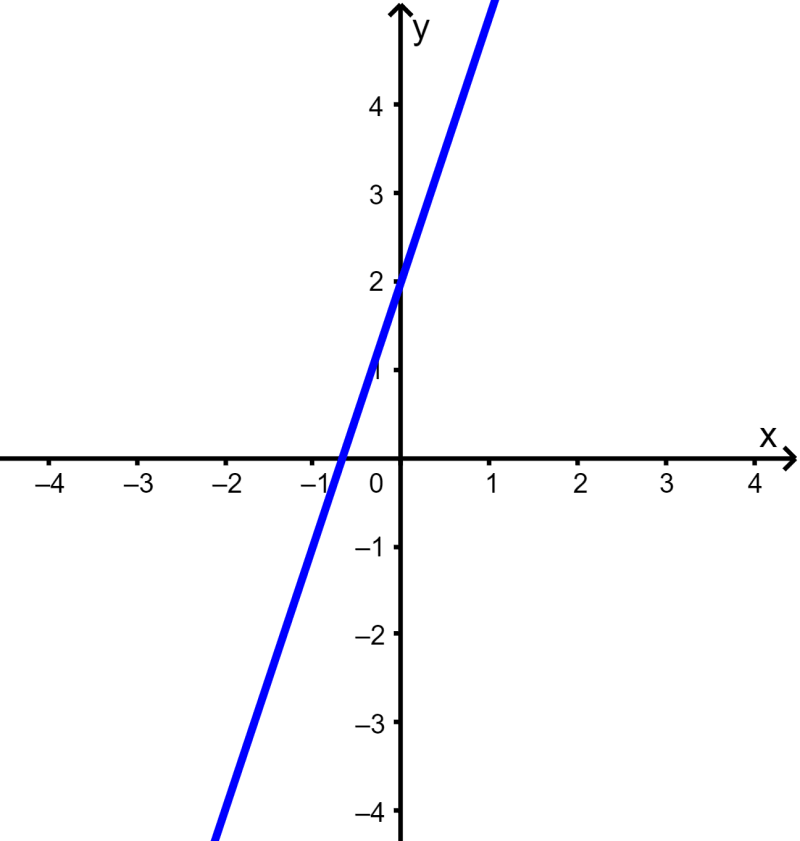
We see that we obtained a straight line, so the equation is a linear function.
EXAMPLE 2
Determine whether the equation $latex 2x-2y=6$ is a linear function.
Solution: We can isolate the dependent variable to facilitate the visualization of the equation. Then, we have:
$latex 2x-2y=6$
$latex -2y=-2x+6$
$latex y=x-3$
We see that we have the variable x with a power of 1, which means that it is a linear function. Looking at its graph we have:
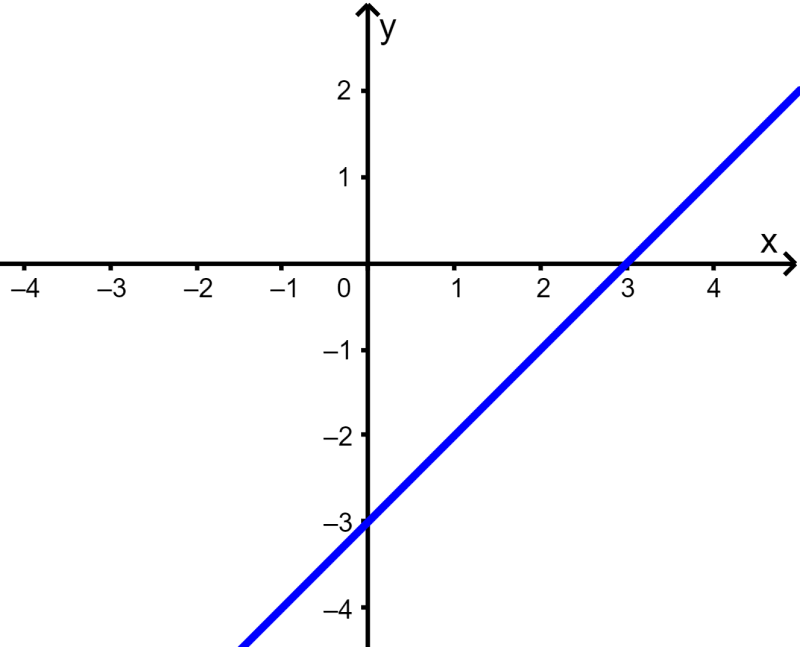
The graph is a straight line, so the equation is a linear function.
EXAMPLE 3
Determine whether the equation $latex y=2{{x}^2}-3$ is a linear function.
Solution: In this case, we see that the variable x has a power of 2. This means that the function is not linear. This is a quadratic function. Let’s look at its graph to verify this:
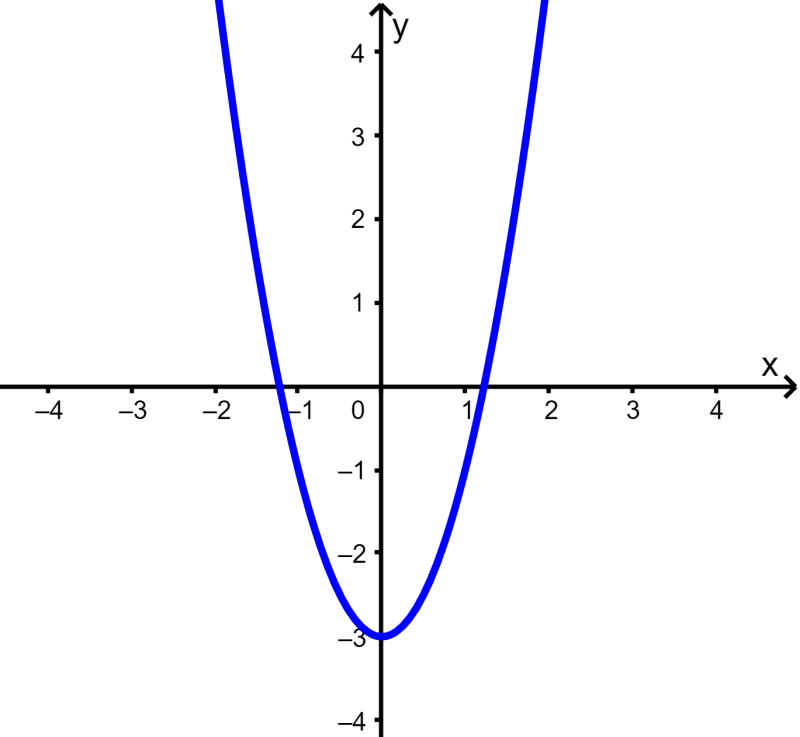
We see that we obtained a parabola, thus, the equation is not a linear function.
EXAMPLE 4
Determine whether the equation $latex 3x(2x+1)+2y=5$ is a linear function.
Solution: We have to simplify and rearrange the equation for easier visualization:
$latex 3x(2x+1)+2y=5$
$latex 6{{x}^2}+3x+2y=5$
$latex 2y=-6{{x}^2}-3x+5$
$latex y=-3{{x}^2}-\frac{3}{2}x+\frac{5}{2}$
Clearly, the equation is not a linear function since the variable x has an exponent of 2. Let’s look at the graph of the function:
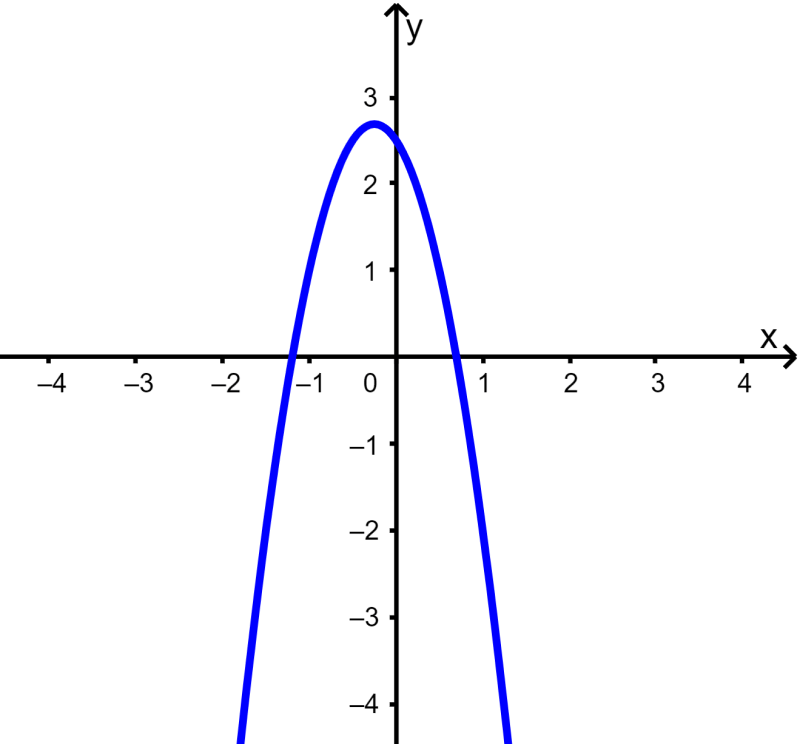
We see that we obtained a parabola, so the equation is not a linear function.
See also
Interested in learning more about functions? Take a look at these pages: