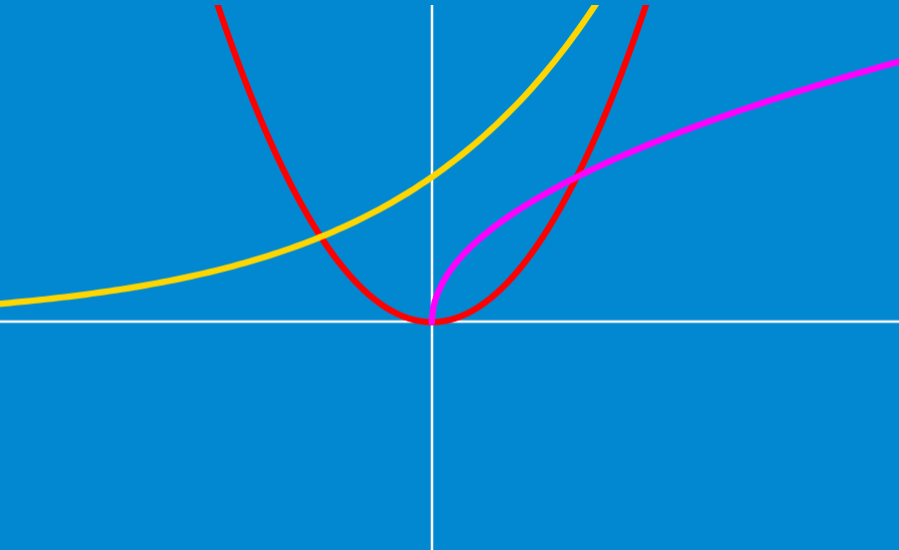
There are several types of algebraic functions that have different characteristics that make them unique. Many of these algebraic functions can be identified just by looking at their graph.
In this article, we will learn about the types of algebraic functions and their graphs along with some of their most important characteristics.
What are functions?
A function is a relationship between a set of inputs and a set of outputs with the property that each input is related to exactly one output. Suppose we have the sets P and Q. Mapping from P to Q will be a function only when each element in the set P has only one element of the set Q assigned.
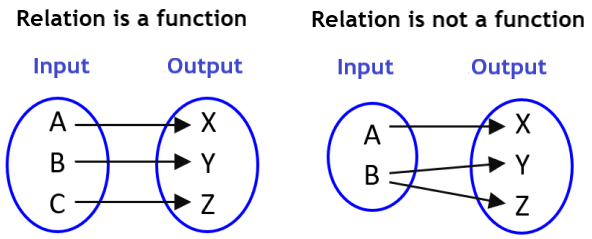
Conditions for a function
The sets P and Q must not be empty.
In a function, a particular input is given to obtain a particular output.
A function f: P → Q denotes that f is a function from P to Q, where P is the domain and Q is the range.
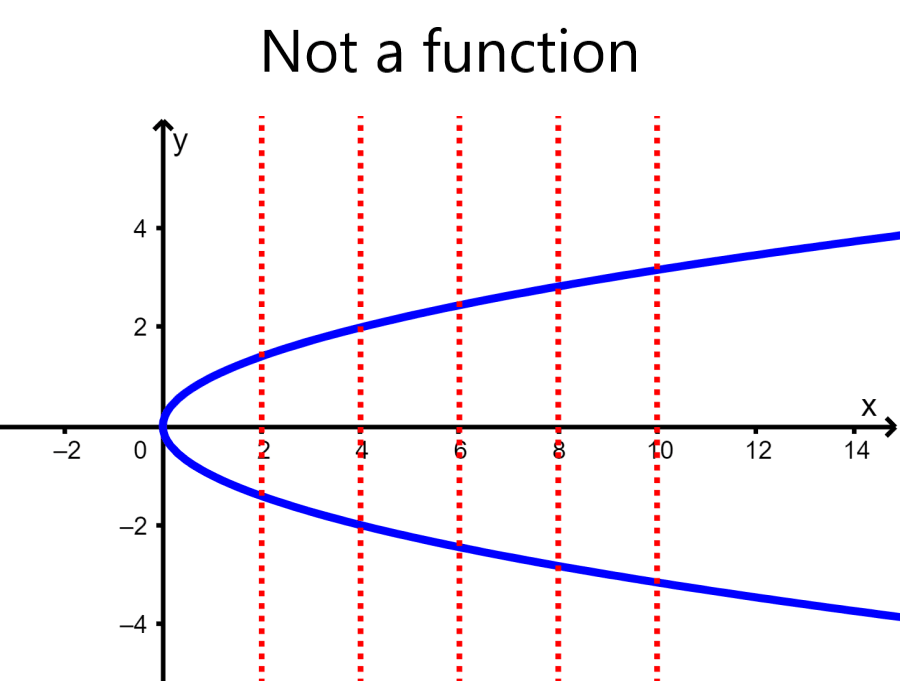
Vertical line test: The vertical line test is used to determine whether a specific curve represents a function or not. For the graph to be a function, any vertical line drawn must cross the graph at only one point.
If it is possible to draw a vertical line that crosses the graph at two or more than two points, the graph is not a function.
Representation of functions
Functions are generally represented as $latex f(x)$.
If we have the function $latex f(x)={{x}^3}$, we read this as “f of x is equal to x cubed”.
Keep in mind that we can use any letter of the alphabet both lowercase and uppercase to represent the functions and their variables. For example, the following are also valid representations of functions:
$latex g(t), ~h(x), ~f(s)$
What are the different types of algebraic functions?
The following are the most important types of algebraic functions:
- Polynomial function
- Constant function
- Linear funtion
- Quadratic function
- Cubic function
- Identity function
- Rational function
- Inverse function
- Exponential function
- Logarithmic function
- Trigonometric functions
- Even and odd functions
- Piecewise functions
- Injective function
- Surjective function
- Bijective function
- Absolute value function
Types of functions and their graphs
Polynomial function
A polynomial function is a function that is a polynomial like
$latex f(x)=a{{x}^3}+b{{x}^2}+cx+d$
The domain of polynomial functions is all real numbers. These functions are continuous throughout their domain.
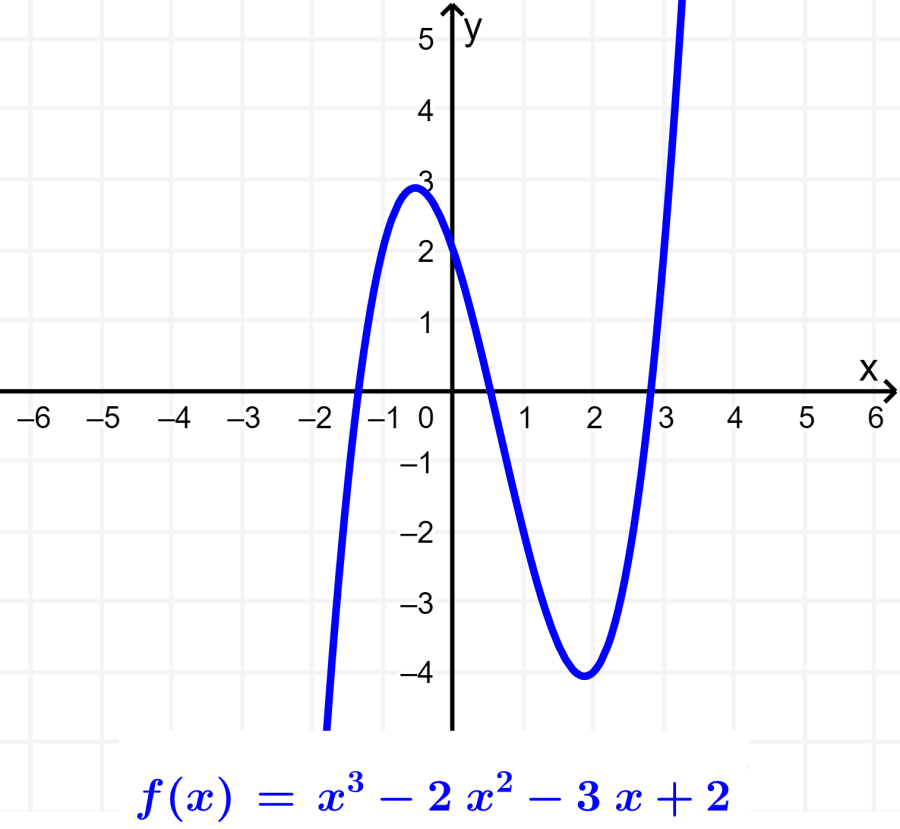
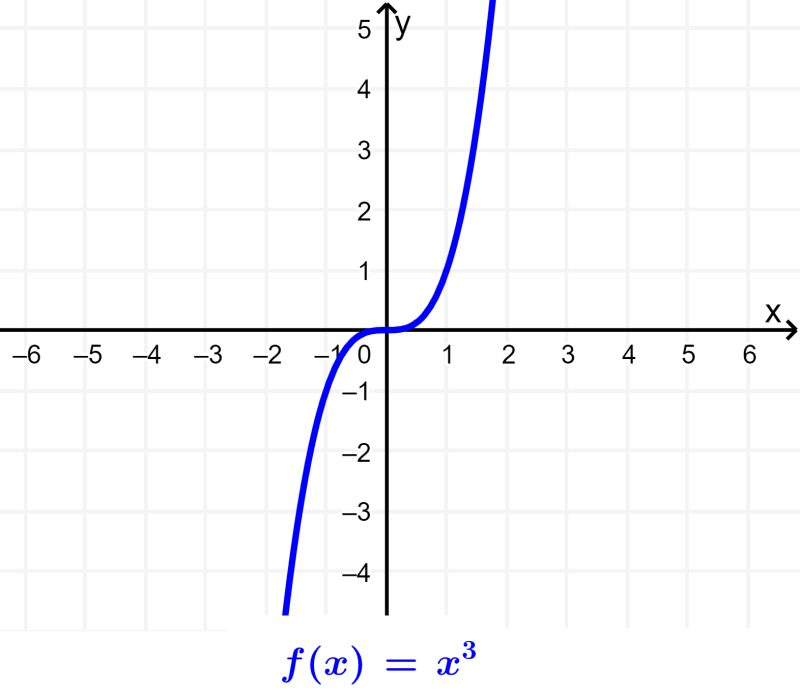
The highest power in the expression is known as the degree of the polynomial function. For example, the following graph represents a third-degree polynomial function:
Constant function
The constant function is a zero degree polynomial function, where we have $latex f(x)=f(0)=c$. No matter what the input value is, the function always returns the same constant value.
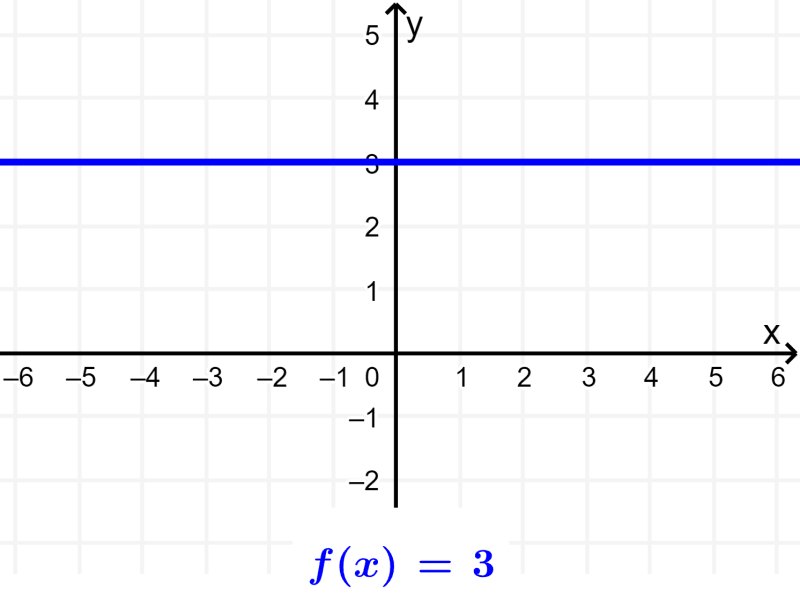
Linear function
All functions of the form $latex f(x)=ax+b$, where a and b are real numbers and a is nonzero, are linear functions. The graph of these functions will always be a straight line. This means that the linear function is a polynomial function of the first degree:
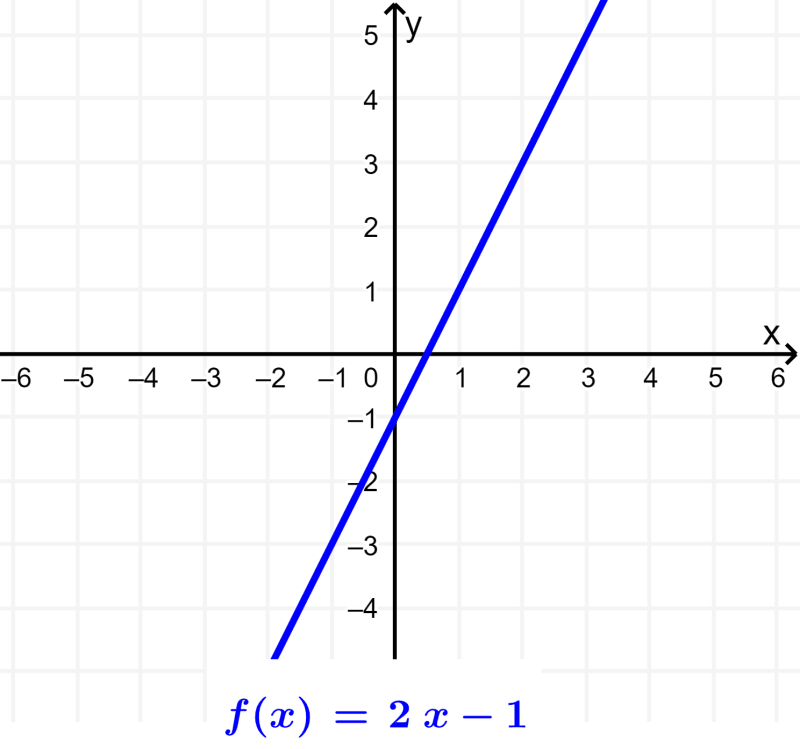
Quadratic function
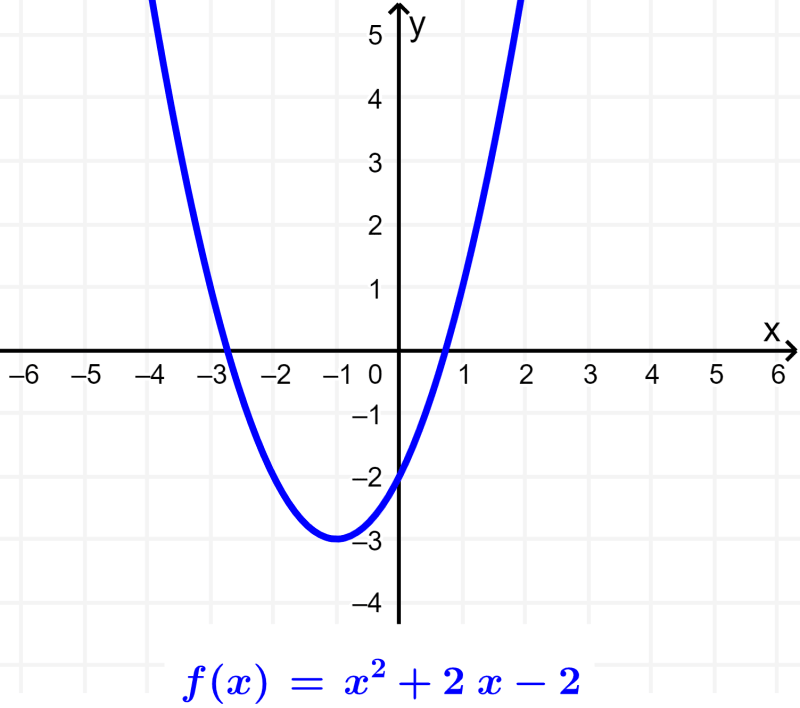
All functions that have the form $latex f(x)=a{{x}^2}+bx+c$, where a, b and c are real numbers and a is nonzero, are quadratic functions. A quadratic function is a second-degree polynomial function, so its graph is a parabola:
Cubic function
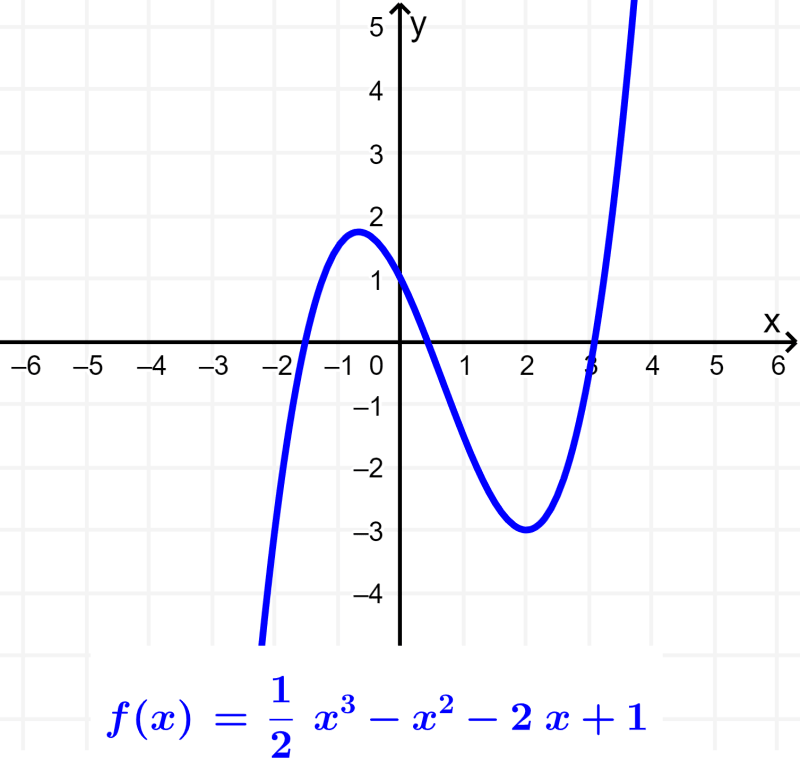
Similar to the previous polynomial functions, the cubic function has the form $latex f(x)=a{{x}^3}+b{{x}^2}+cx+d$, where a, b, c, and d are real numbers and a is different from zero. This function is a third-degree polynomial function:
Identity function
An identity function is a function in which the image of any element is that same element: $latex f(x)=x$.
The identity function is a linear function with slope $latex m=1$ that passes through the point (0, 0). This function divides the first and third quadrants into equal parts:
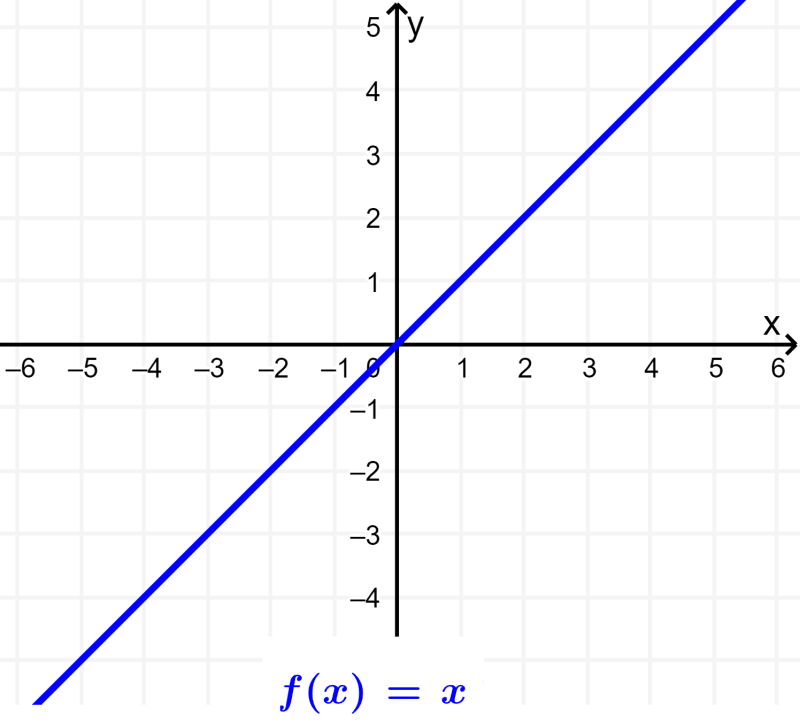
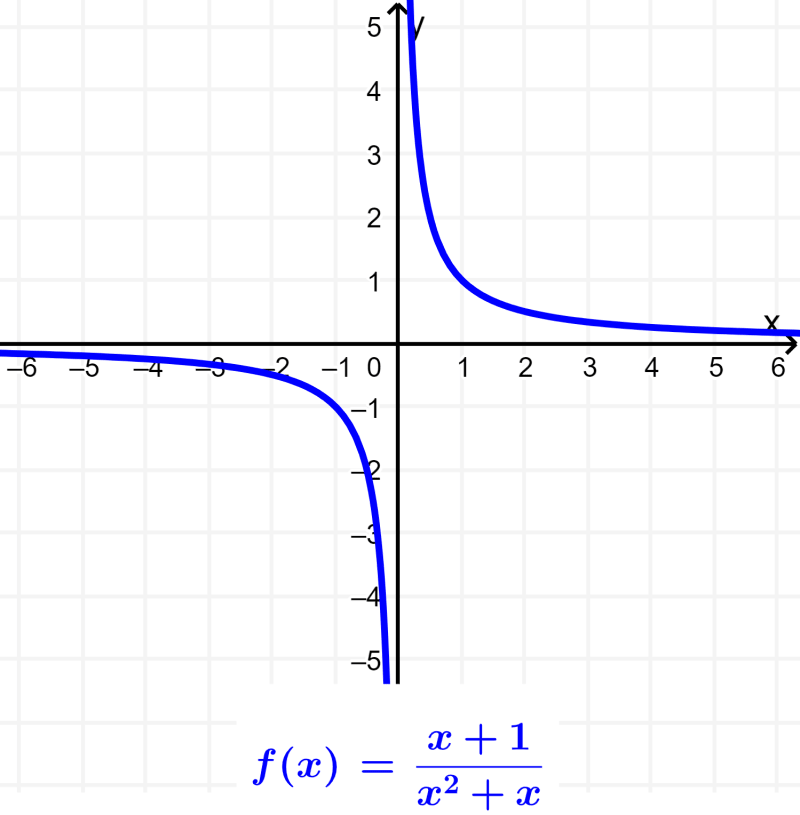
Rational function
Rational functions are functions that are represented as fractions of two polynomials, $latex f(x)=\frac{{P(x)}}{{Q(x)}}$, where the quotient is irreducible and $latex Q(x)$ is different from zero. The domain of a rational function is all real numbers except the numbers that make the denominator equal to zero.
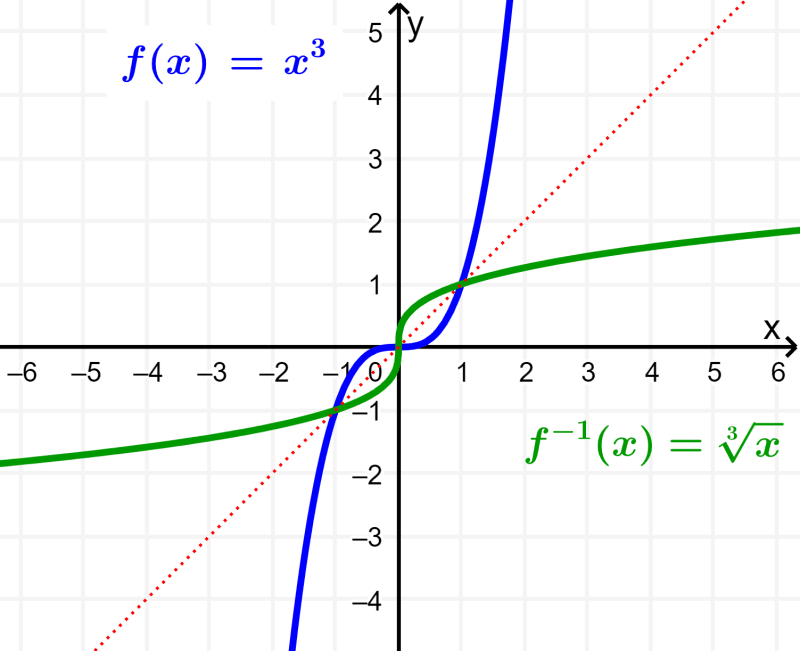
Inverse function
An inverse function is a function that reverses the effect of the original function. For example, if the original function multiplies by 3, the inverse function divides by 3, and if the original function multiplies by 3 and then adds 4, then the inverse function subtracts 4 and then divides by 3.
The following is the graph of the function $latex f(x)={{x}^3}$ and its inverse:
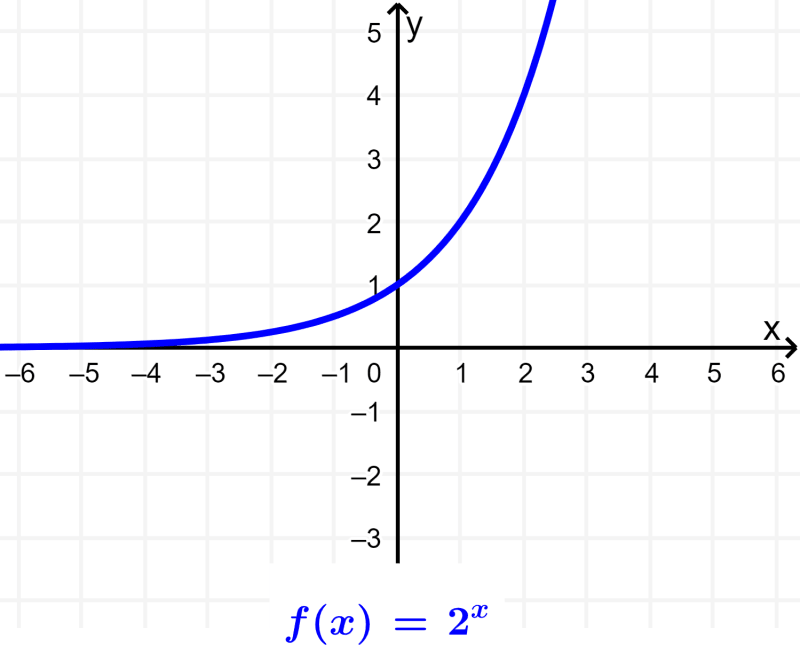
Exponential function
Exponential functions are functions that have the variable as the exponent of a base. These functions have the general form $latex f(x)={{b}^x}$, where b is the base of the exponential function.
Logarithmic function
A logarithmic function is made up of a logarithm with base b. In its simplest form, the logarithmic function has the form $latex f(x)=\log_{b}(x)$.
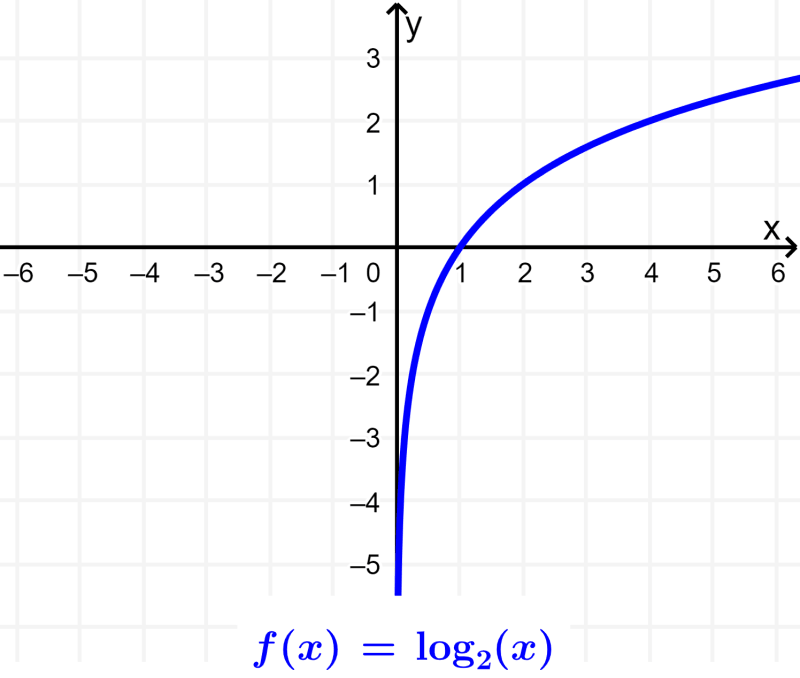
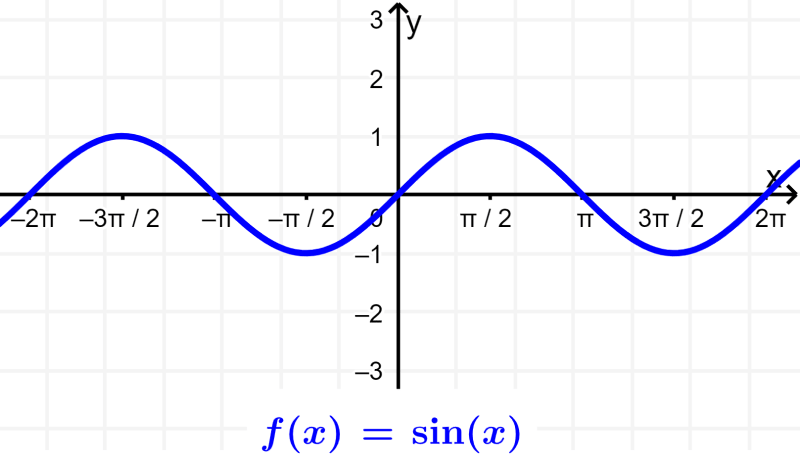
Trigonometric functions
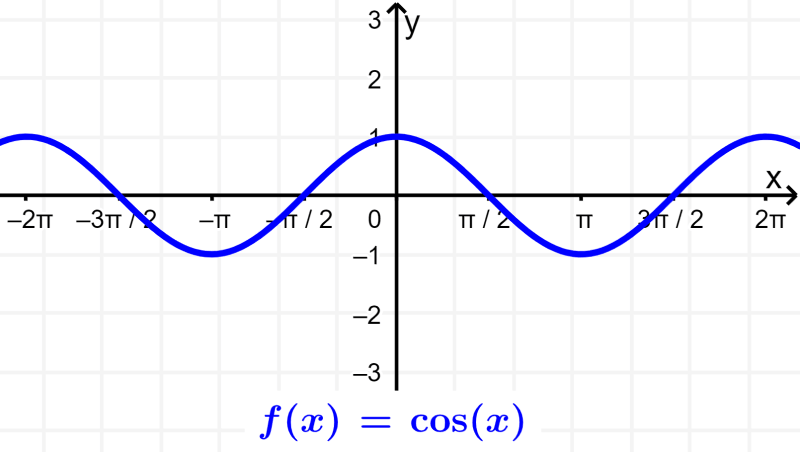
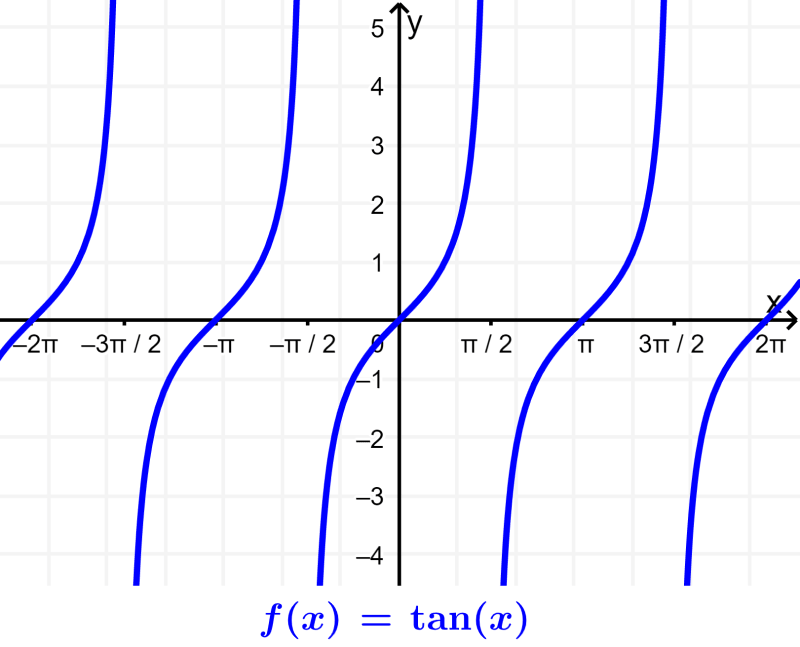
Trigonometric functions are functions that are obtained from different relationships of the three sides of a right triangle. The six main trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent.
Sine: The sine of an angle is defined as the ratio between the opposite side (O) and the hypotenuse (H). $latex \sin(\theta)=\frac{O}{H}$.
Cosine: The cosine of an angle is defined as the ratio between the adjacent side (O) and the hypotenuse (H). $latex \cos(\theta)=\frac{A}{H}$.
Tangent: The tangent of an angle is defined as the ratio between the opposite side (O) and the adjacent side (A). $latex \tan(\theta)=\frac{O}{A}$.
Cosecant: The cosecant is the reciprocal trigonometric ratio of the sine. The cosecant is defined as the ratio between the hypotenuse (H) and the opposite side (H). $latex \csc(\theta) =\frac{H}{O}$.
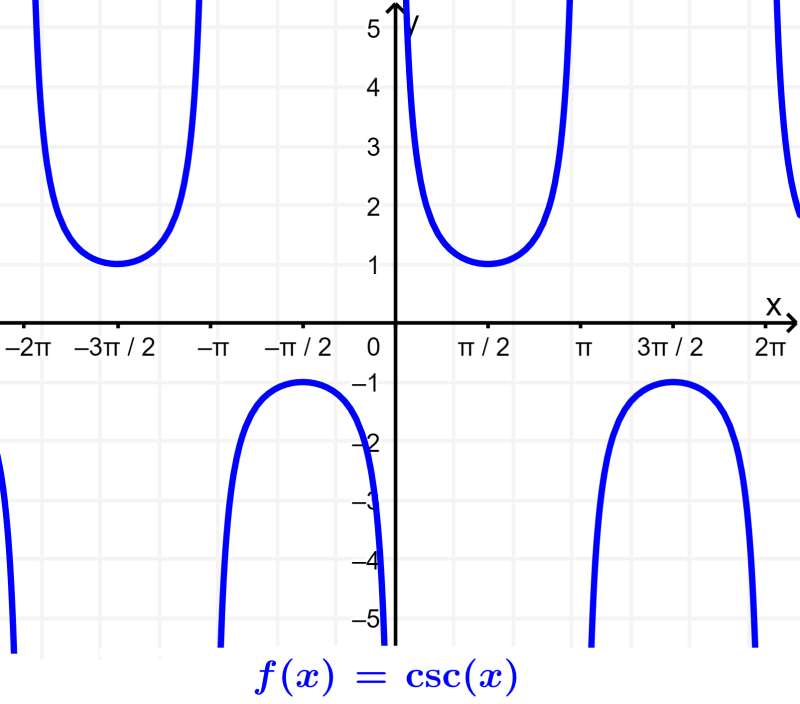
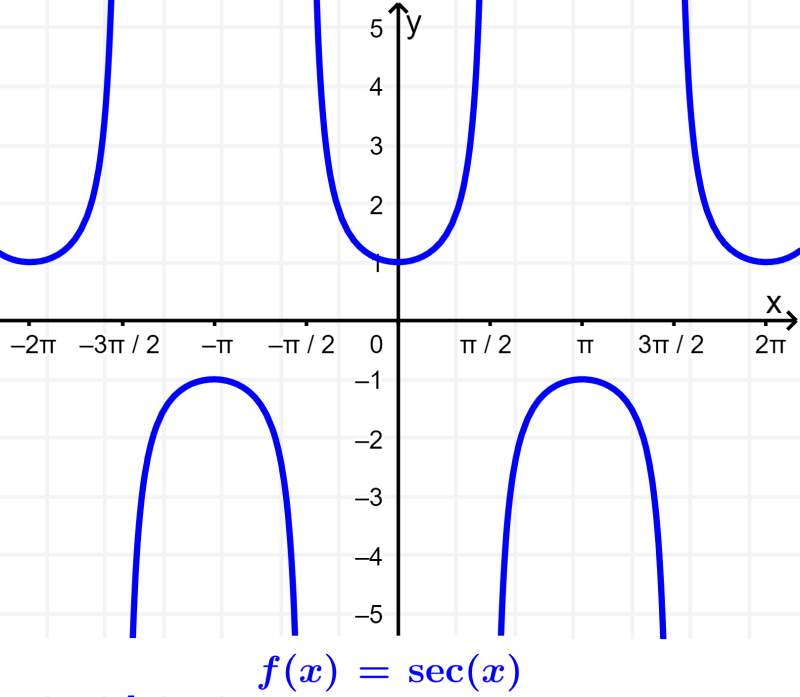
Secant: The secant is the reciprocal trigonometric ratio of the cosine. The secant is defined as the ratio between the hypotenuse (H) and the adjacent side (A). $latex \sec(\theta)=\frac{H}{A}$.
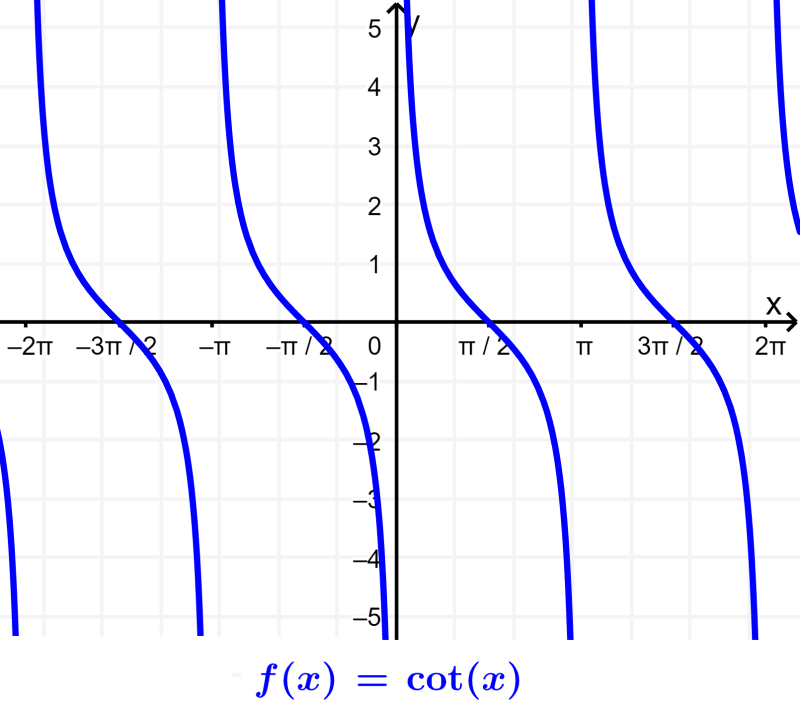
Cotangent: The cotangent is the reciprocal trigonometric ratio of the tangent. The cotangent is defined as the ratio between the adjacent side (A) and the opposite side (O). $latex \cot(\theta)=\frac{A}{O}$.
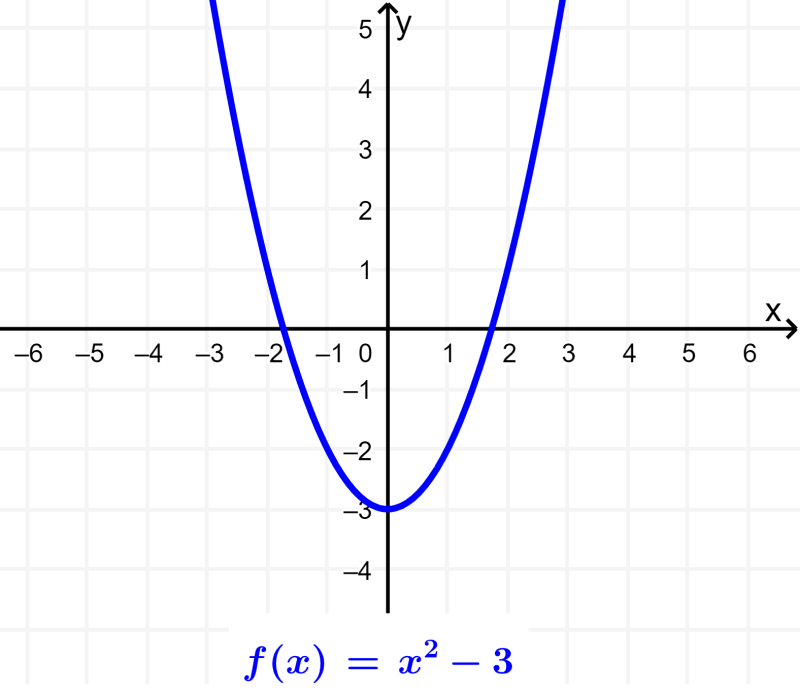
Odd and even functions
If we have that $latex f(x)=f(-x)$, then the function will be even. The even function is symmetric about the y-axis.
If we have that $latex -f(x)=f(x)$, then the function will be odd. The odd function is symmetric about the origin.
Piecewise function
Piecewise functions, also known as functions defined by parts, are functions that have different expressions depending on the interval in which the independent variable is found.
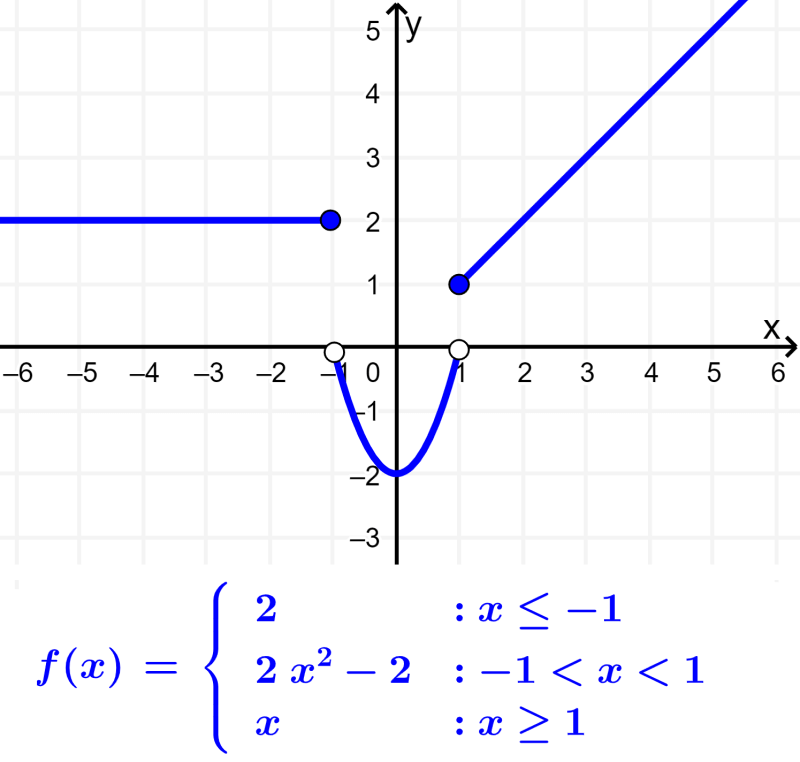
Absolute value function
The absolute value function causes the outputs of the function to always be positive. In its simplest form, the absolute value function has the form $latex f(x)=|x|$. This function forms a V-shaped graph.
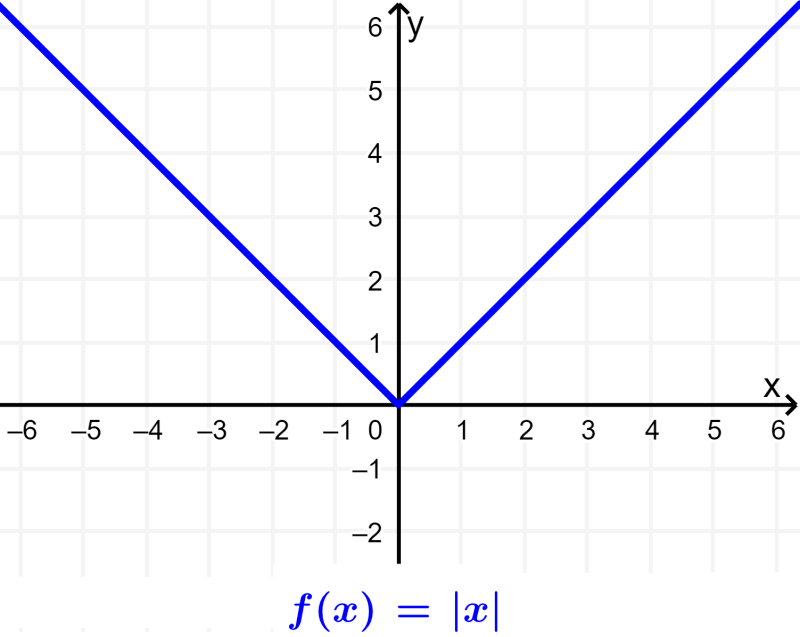
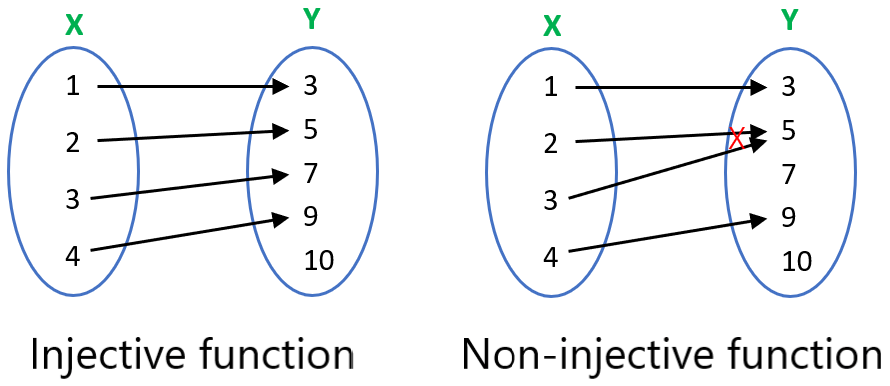
Injective function
The injective function is a function in which each element of the final set (Y) has a single element of the initial set (X). These functions are also known as one-to-one.
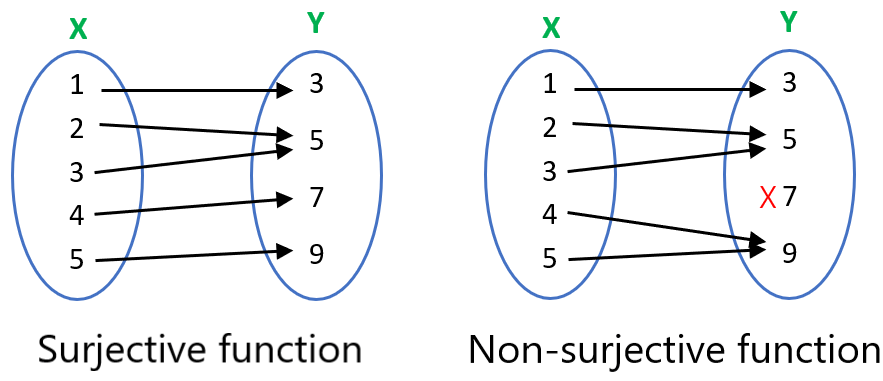
Surjective function
A surjective function is a function in which all the elements of the final set (Y) have at least one element of the initial set (X) corresponding to them.
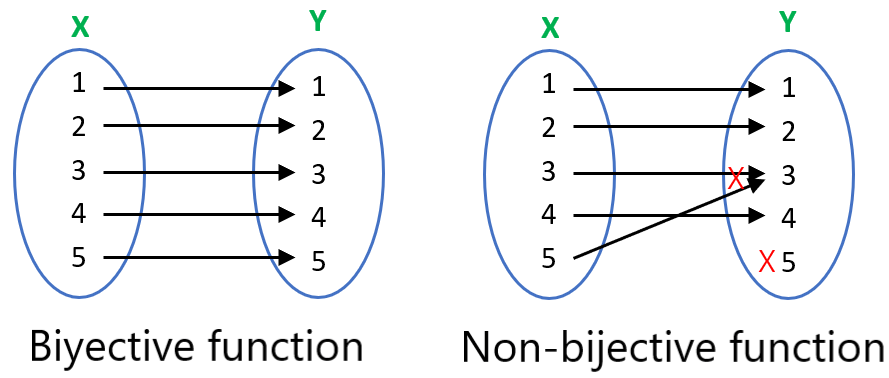
Bijective function
A bijective function is a function that is injective and surjective at the same time.
See also
Interested in learning more about functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
