The horizontal and vertical translation is a transformation that allows us to modify the graph of the original function. Given the function f(x), we can translate the function horizontally with the transformation f(x+a) and vertically with the transformation f+a where a is a value that can be positive or negative.
Here, we will learn everything related to the horizontal and vertical translation of a function. We will look at some examples to illustrate the concepts.
ALGEBRA
Relevant for…
Learning about the horizontal and vertical translation of functions.
ALGEBRA

Relevant for…
Learning about the horizontal and vertical translation of functions.
Determining the horizontal translation of a function
The horizontal translation in a function is a transformation that produces a shift to the left or to the right of the original function. That is, the translation occurs parallel to the x-axis.
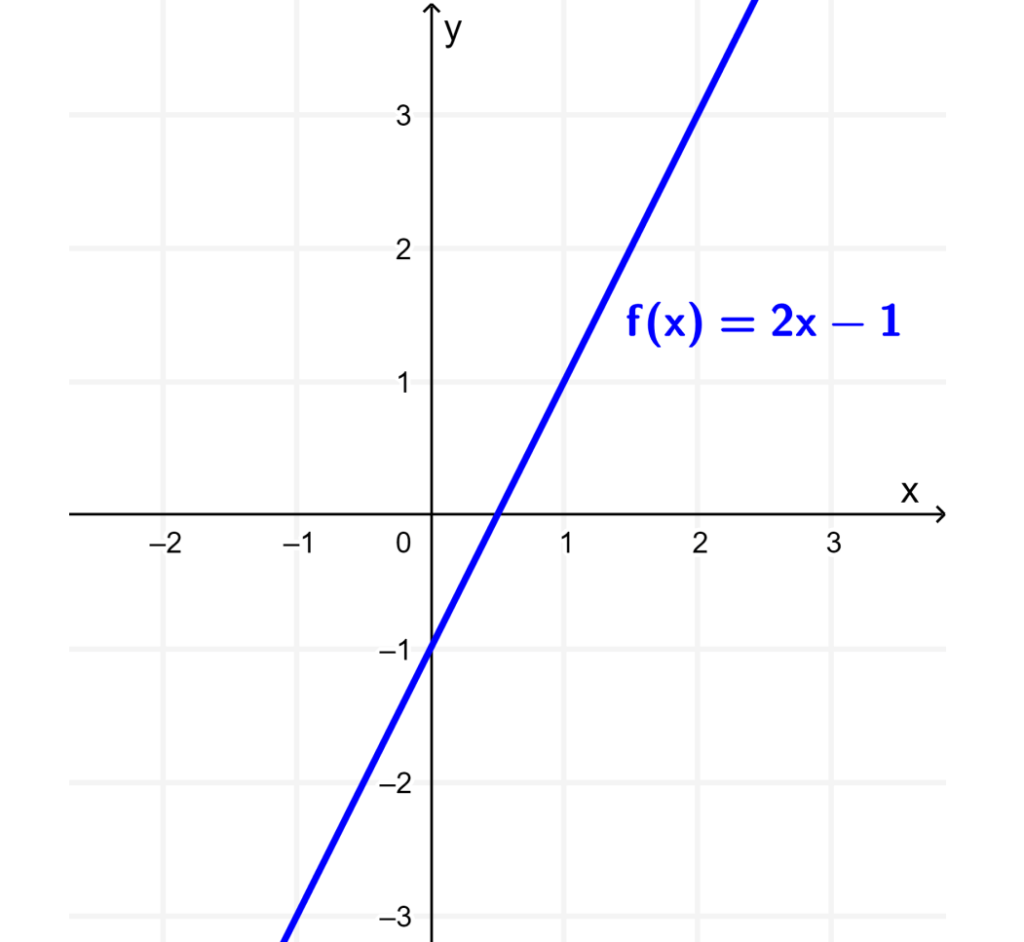
We can understand the horizontal translation of a function by taking the function $latex f(x)=2x-1$ as an example. When we graph this function, we get the following line:
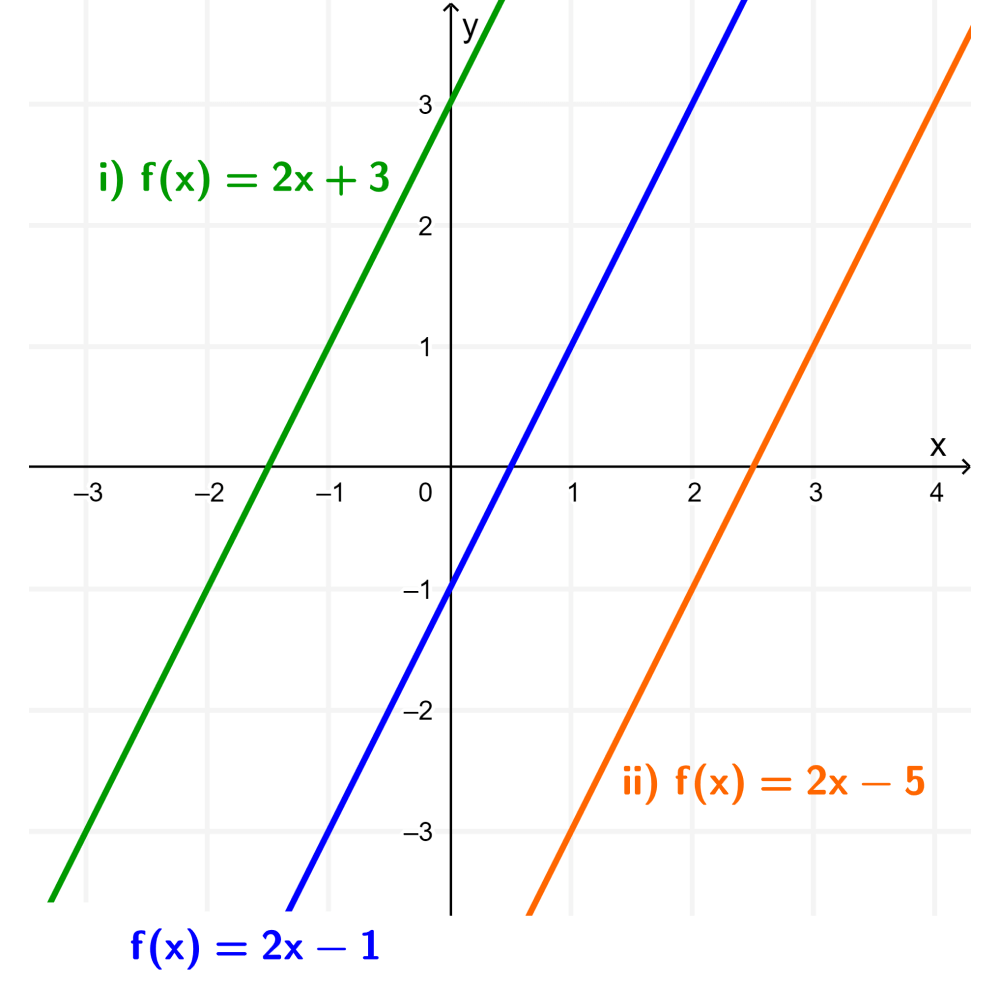
Now, we are going to apply the transformations (i) $latex f(x+2)$ and (ii) $latex f(x-2)$. Therefore, using the original function $latex f(x)=2x-1$ and simplifying the transformations, we have:
(i) $latex f(x+2)=2(x+2)-1~$ and (ii) $latex f(x-2)=2(x-2)-1$
(i) $latex f(x+2)=2x+3~$ and (ii) $latex f(x-2)=2x-5$
We can then graph functions (i) and (ii) using the same coordinate plane as the original function to compare their graphs. Therefore, we have:

In case (i), the transformation $latex f(x+2)$ produced a translation of 2 units to the left. That is, -2 units parallel to the x-axis.
In case (ii), the transformation $latex f(x-2)$ produced a translation of 2 units to the right. That is, 2 units parallel to the x axis.
In short, we have:
- The transformation $latex f(x+a)$ results in a shift in the original graph of f of $latex a$ units to the left.
- The transformation $latex f(x-a)$ results in a shift in the original graph of f of $latex a$ units to the right.
Determining the vertical translation of a function
The vertical translation of a function is a transformation that causes the graph of the original function to be moved up or down. That is, the translation occurs parallel to the y-axis.
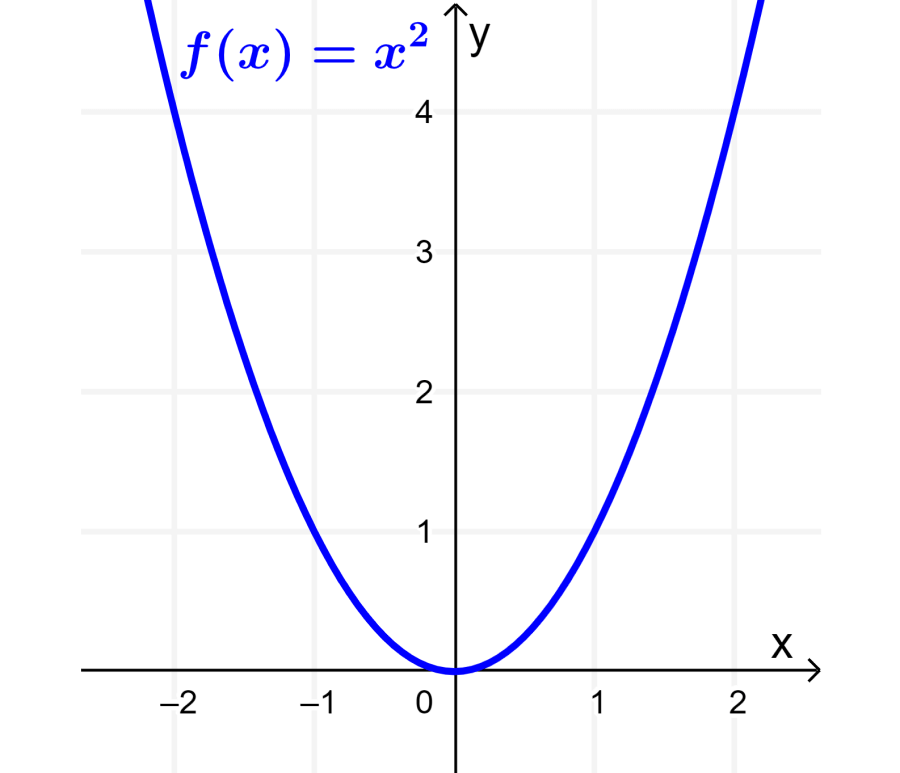
To understand the vertical translation of a function, we can consider the function $latex f(x)=x^2$ as an example. If we graph this function, we get the following curve:
If we now add and subtract 1 unit from the original function, we have the functions (i) $latex f(x)+1$ and (ii) $latex f(x)-1$. Simplifying, we have:
(i) $latex f(x)+1=x^2+1~$ and (ii) $latex f(x)-1=x^2-1$
Using the same Cartesian plane as the original function $latex f(x)$, we can graph functions (i) and (ii) to obtain the following:
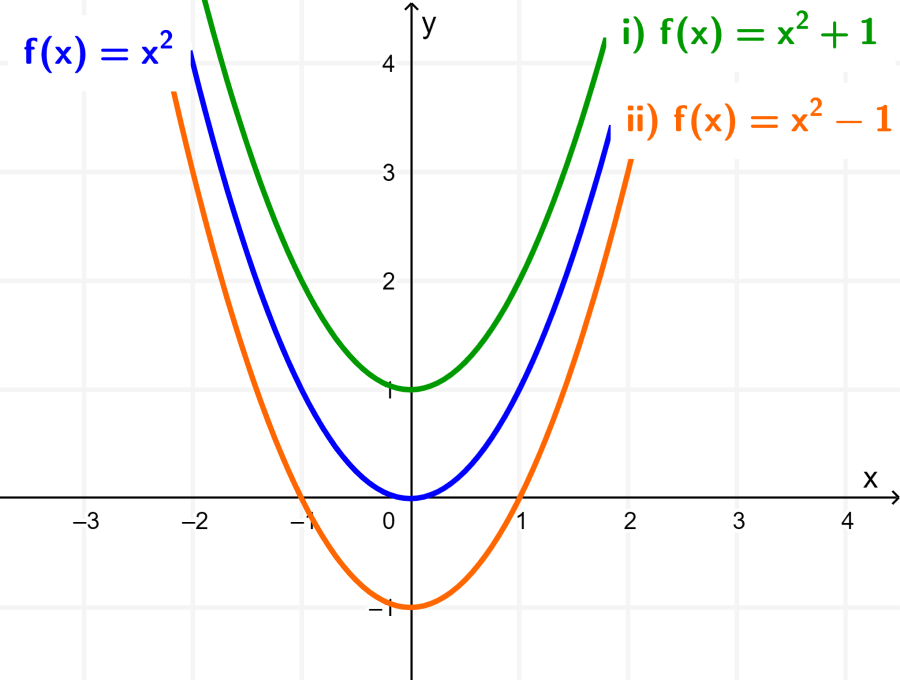
We can see that, in case (i), the graph of f has been moved up 1 unit. That is, 1 unit parallel to the y-axis.
On the other hand, the graph of the function (ii) is equal to the graph of f moved down 1 unit. That is, -1 unit parallel to the y-axis.
In short, we have the following:
- The transformation $latex f(x)+a$ produces a shift in the original graph of $latex f(x)$ of $latex a$ units up.
- The transformation $latex f(x)-a$ produces a shift in the original graph of $latex f(x)$ of $latex a$ units down.
Examples of horizontal and vertical translation in functions
EXAMPLE 1
Sketch the graph of $latex f(x)=x^2-1$. Then, find the equation of the transformation $latex g(x)=f(x+2)$ and graph it.
Solution
Starting with the graph of $latex f(x)$, we have:
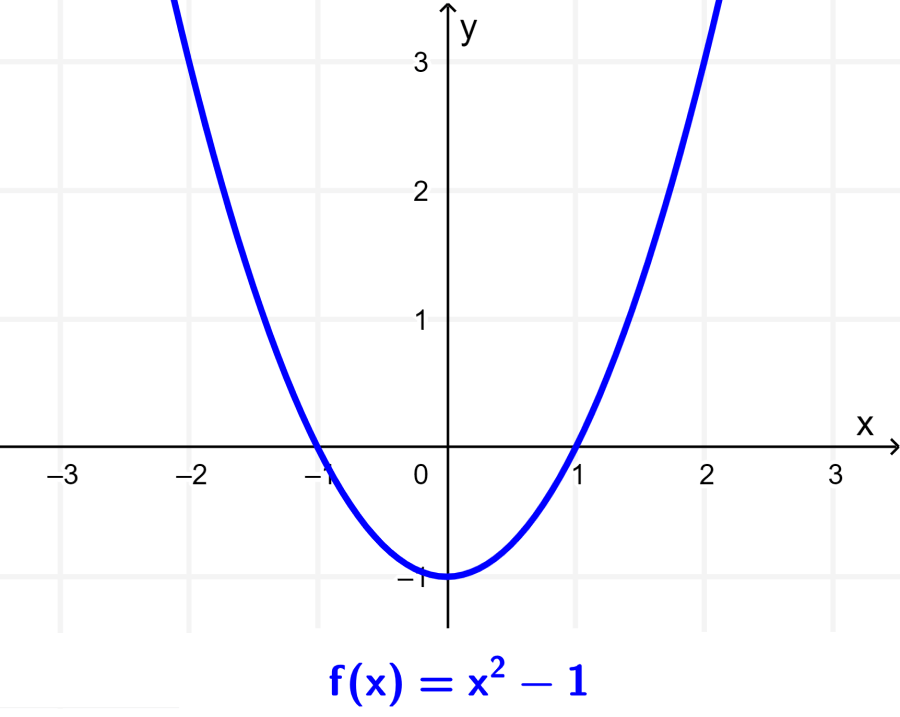
Now, we can find the equation of the function $latex g(x)$ by applying the transformation on the original function and simplifying:
$latex g(x)=f(x+2)$
$latex =(x+2)^2-1$
$latex =x^2+4x+4-1$
$latex =x^2+4x+3$
We can graph the function $latex g(x)$ by considering that the graph of g can be obtained by translating the graph of f by 2 units to the left, that is, -2 units on the x-axis.
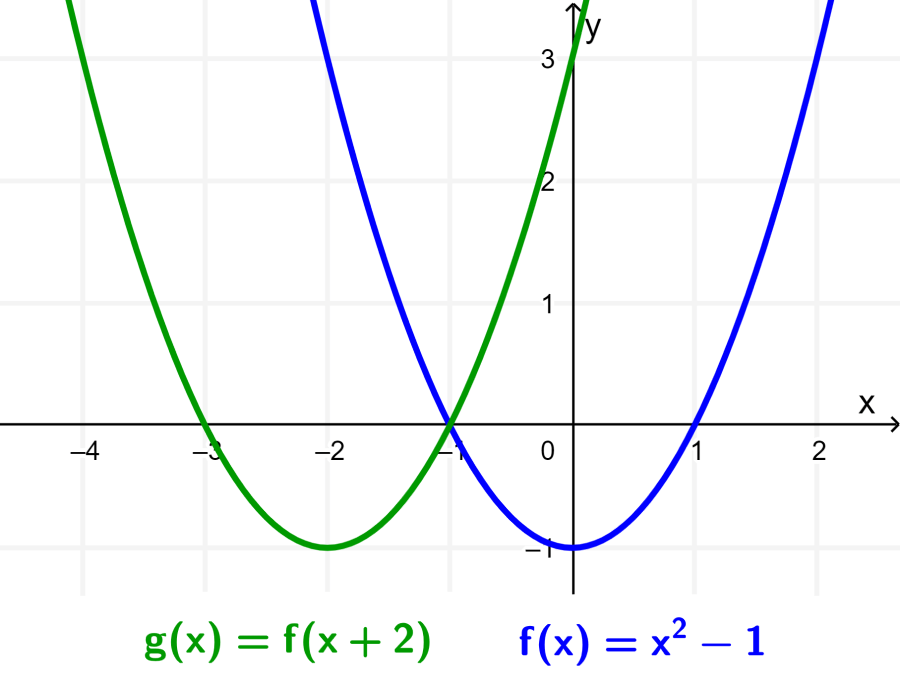
.
EXAMPLE 2
We have the function $latex f(x)=x^3$. If we have the function $latex g(x)=x^3-3$, get the graphs of g and f.
Solution
Function f is the base cubic function. This function is plotted on the left side of the following diagram.
In the case of function g, we can see that this function is equivalent to the function f with a vertical translation of -3 units, as we can see on the right-hand side of the graph in the following diagram.
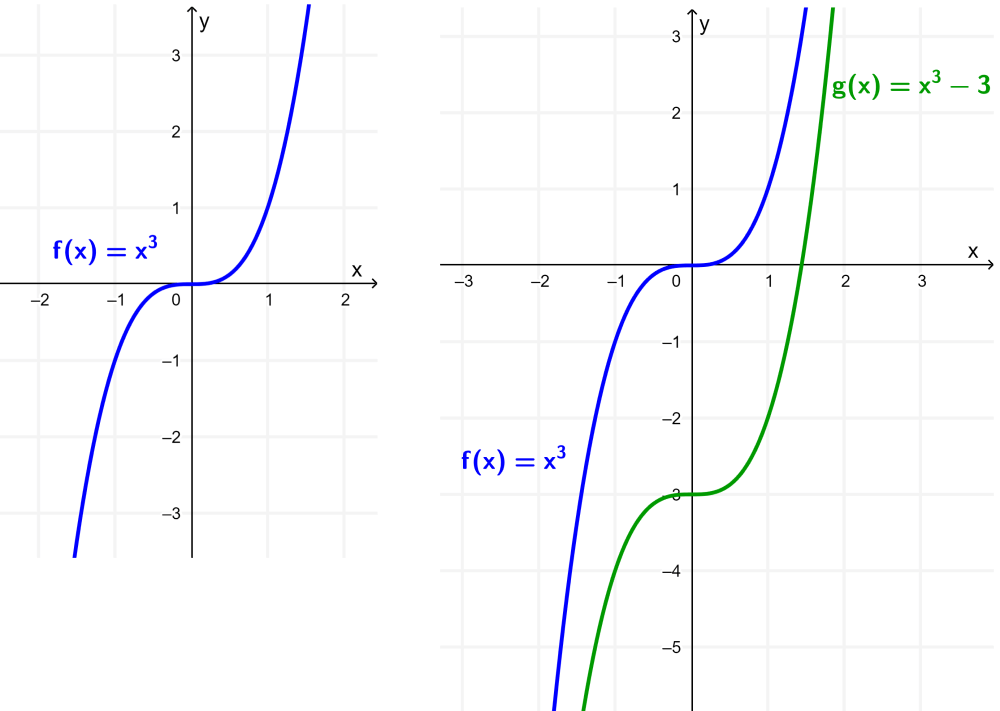
.
EXAMPLE 3
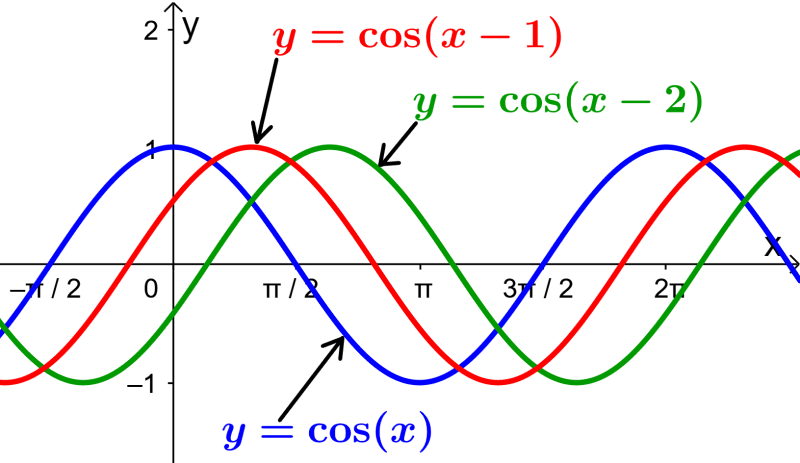
Graph the cosine function in its base form. Then graph two cosine functions that are shifted 1 unit and 2 units to the right from the base shape.
Solution
The base cosine function, $latex f(x)=cos(x)$, has a value of 1 when x equals 0. Also, it passes through the point (π/2, 0) and has a period of π.
To apply a horizontal translation of 1 unit and 2 units to the right, we have to apply the transformations $latex g(x)=f(x-1)$ and $latex h(x)=f(x-2)$ respectively.
When we graph the three functions, we have:
EXAMPLE 4
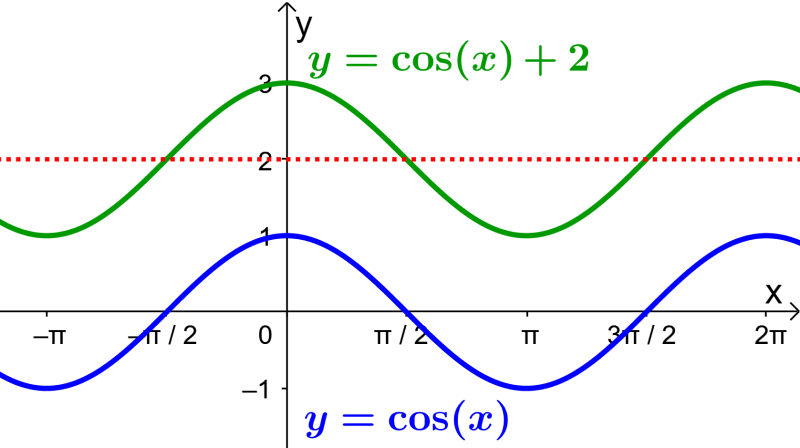
Graph the function $latex f(x)=\cos(x)+2$.
Solution
By comparing the given function to the standard cosine function $latex f(x)=\cos(x)$, we can deduce that a vertical translation of 2 units up was applied.
Therefore, we can graph the function $latex f(x)=\cos(x)+2$ by graphing a basic cosine function and moving it 2 units up:
EXAMPLE 5
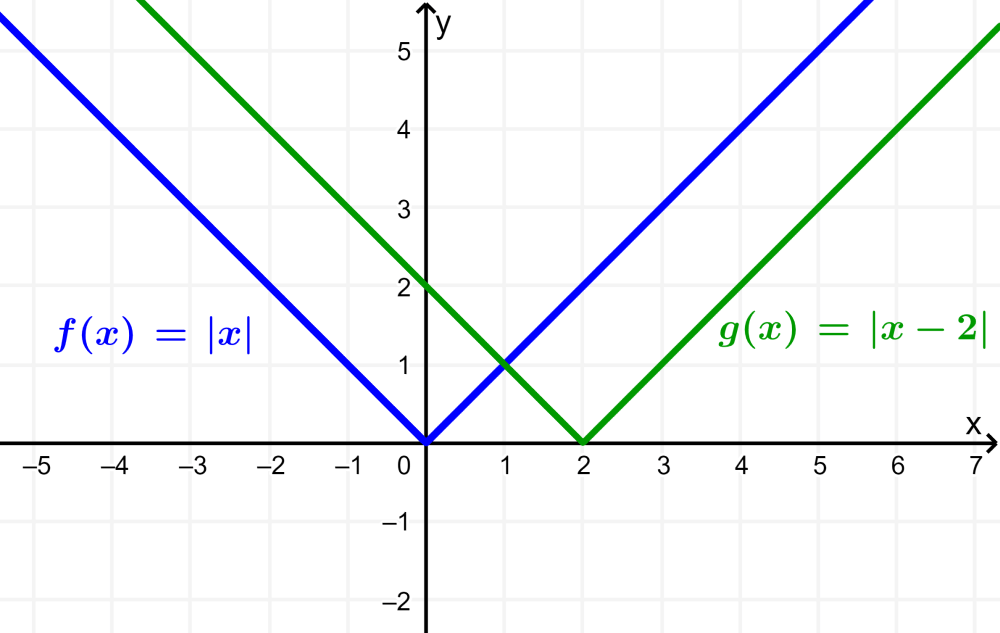
Obtain the graph of $latex g(x)=|x-2|$.
Solution
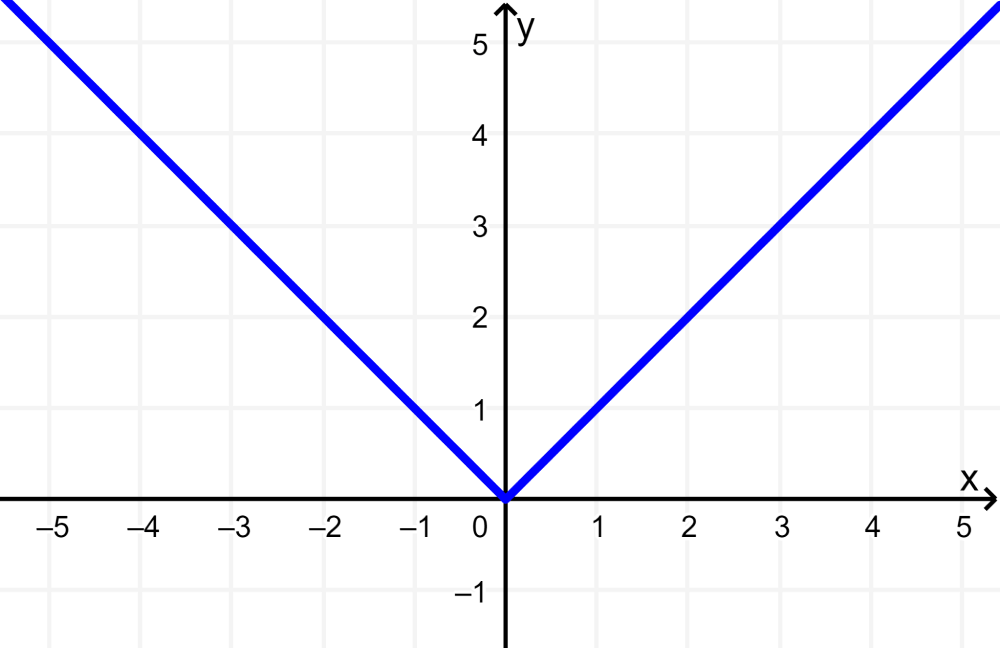
In this example, we have the absolute value function. In its base form, $latex f(x)=|x|$, the graph of the absolute value function is:
Therefore, the graph of $latex g(x)=|x-2|$ can be obtained by shifting the graph of the absolute value function 2 units to the right when compared to the base form:
.
EXAMPLE 6
What is the graph of $latex g(x)=|x|-2$?
Solution
Here, we have the absolute value function. In its base form, $latex f(x)=|x|$, the graph of the absolute value function is as follows:

Therefore, we can get the graph of $latex g(x)=|x|-2$ if we move the graph of the base absolute value function down 2 units:

.
EXAMPLE 7
What transformation do we need to apply to shift the function $latex f(x)=\tan(5x-2)$, -4 units parallel to the x-axis?
Solution
A shift of -4 units parallel to the x-axis is equivalent to applying a horizontal translation of 4 units to the left.
We can accomplish this translation by applying the $latex f(x-4)$ transformation. In this case, we have the function $latex f(x)=\tan(5x-2)$. Therefore, we have:
$latex f(x-4)=\tan(5(x-4)-2)$
$latex f(x-4)=\tan(5x-20-2)$
$latex f(x-4)=\tan(5x-22)$
EXAMPLE 8
What transformation do we need to apply to the function $latex f(x)=\tan(5x-2)$ if we want to shift it -5 units parallel to the y-axis?
Solution
A shift of -5 units parallel to the y-axis is the same as applying a shift of 5 units down on the original function.
To perform this shift, we apply the transformation $latex f(x)-5$. In this case, we have the function $latex f(x)=\tan(5x-2)$. Therefore, we have:
$latex f(x)-5=\tan(5x-2)-5$
Horizontal and vertical translation of functions – Practice problems


Which function has a translation of 6 units up with respect to the function $latex f(x)=-2x-3$?
Write the answer in the input box.
See also
Interested in learning more about function transformations? Take a look at these pages:



