The transformation of a function allows us to make modifications to its graph. One of these transformations is the stretching and compression of functions. We can compress or stretch the function on the x-axis when we have f(ax) and we can compress or stretch the function on the y-axis when we have af(x) where a is a constant.
In this article, we will learn how to stretch or compress a function both with respect to the x-axis and with respect to the y-axis.
Stretches and compressions of a function with respect to the x-axis and the y-axis
Stretches and compressions are transformations that are produced when the x or y values of the original function are multiplied by a constant value.
To understand the stretches and compressions with respect to the x-axis and the y-axis, we are going to use the function $latex f(x)=x+1$. By graphing this function, we get the following line:
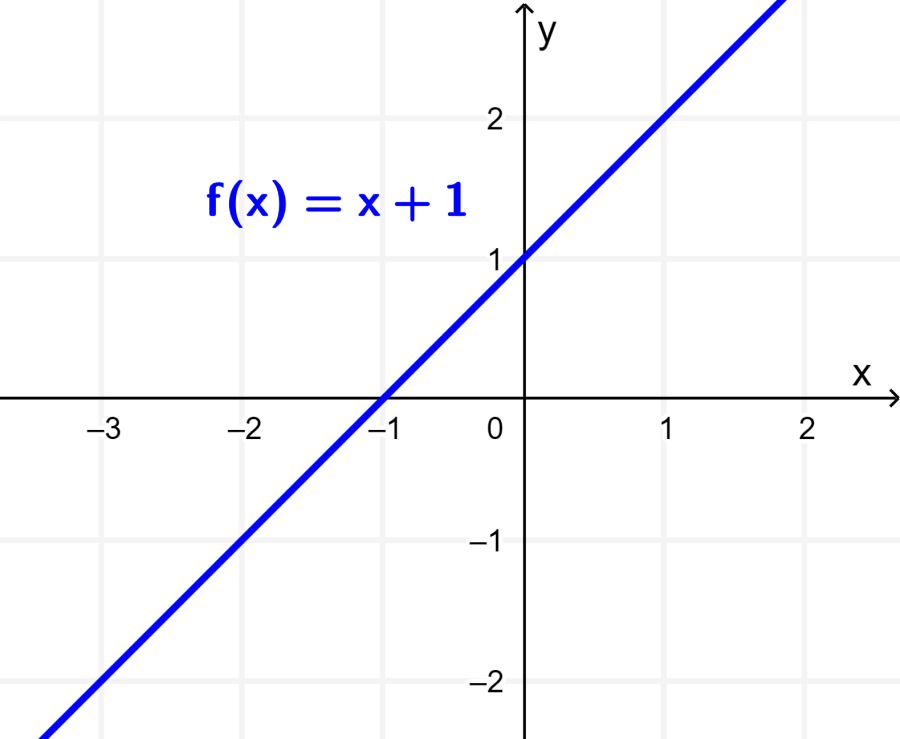
To produce stretches and compressions, we are going to multiply by a constant either the x-values or y-values of the function $latex f(x)$. Therefore, we have (i) $latex f(2x)$ and (ii) $latex 2f(x)$. Simplifying, we have:
(i) $latex f(2x)=(2x)+1~$ and (ii) $latex 2f(x)=2(x+1)$
(i) $latex f(2x)=2x+1~$ and (ii) $latex 2f(x)=2x+2$
When we plot functions (i) and (ii) together with the original function $latex f(x)$, we have:
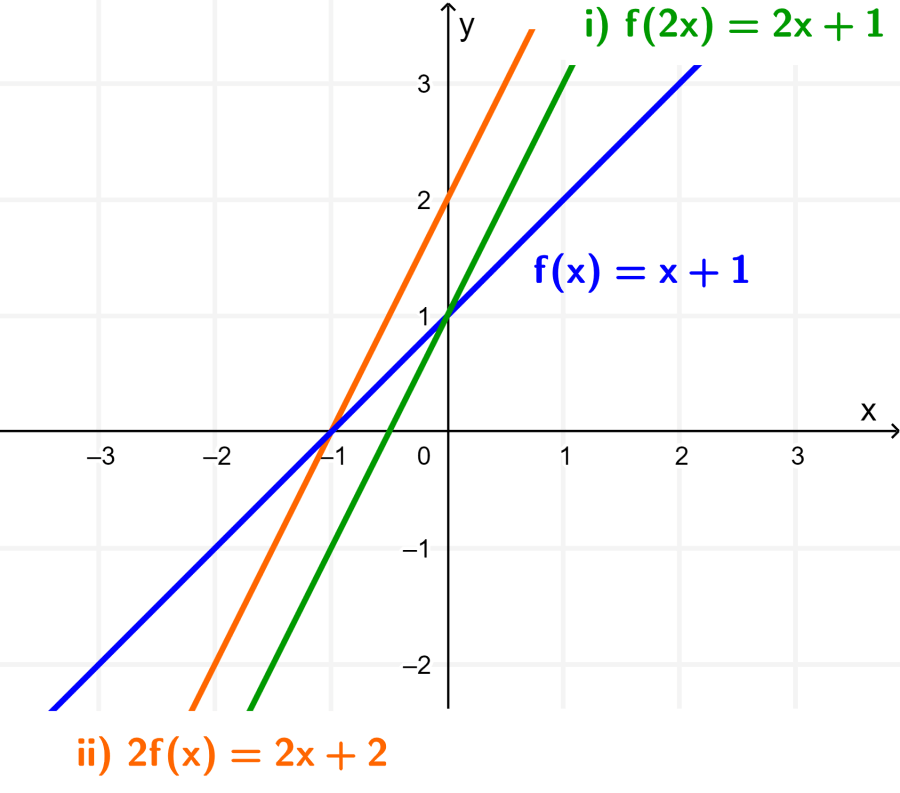
In transformation (i), the graph of $latex f(x)$ has been stretched about the x-axis by a factor of $latex \frac{1}{2}$ (the function was halved)
In transformation (ii), the graph of $latex f(x)$ has been stretched about the y-axis by a factor of 2.
In short, we have:
- The transformation $latex f(ax)$ results in a stretch about the x-axis by a factor of $latex \frac{1}{a}$.
- The transformation $latex af(x)$ results in a stretch about the y-axis by a factor of $latex a$.
- If the stretch factor is between 0 and 1, the transformation is a compression of the graph.
Examples of stretching and compressing functions
The following examples use the function stretch and compress transformations. Each example has a detailed solution, but try to solve the problems yourself first.
EXAMPLE 1
Obtain the graph of the function $latex f(x)=x+2$, and then graph the function $latex g(x)=3f(x)$.
Solution
The graph of the function $latex f(x)=x+2$ is a line that intersects the y-axis at (0, 2) and the x-axis at (-2, 0):
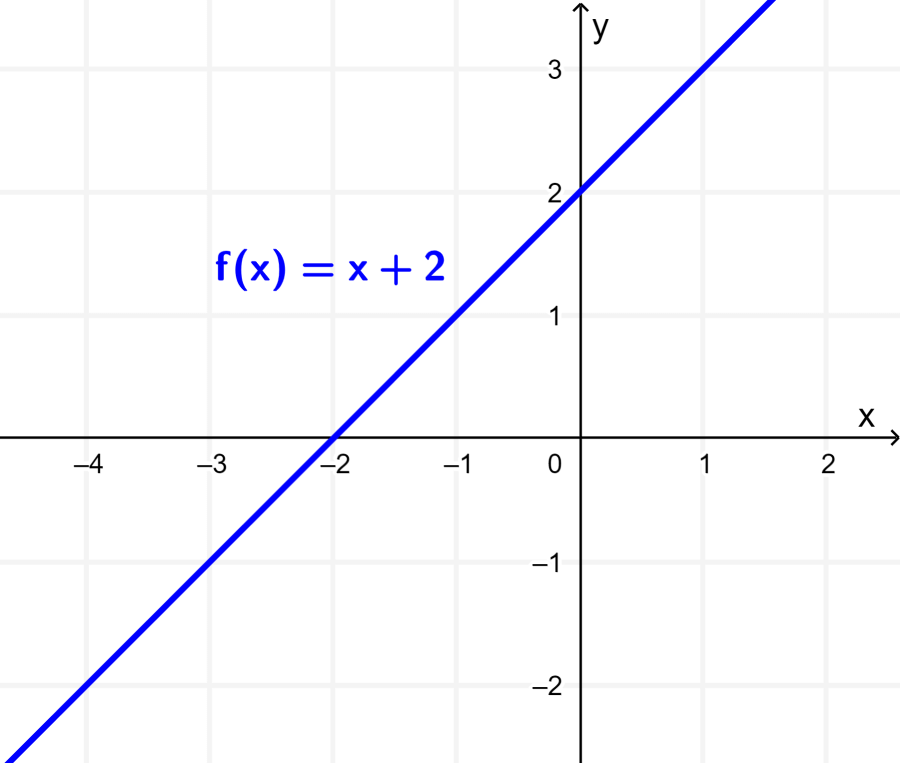
The function g is given by $latex g(x)=3f(x)=3x+6$. The graph of this function is equal to the graph of f stretched by a factor of 3 about the y-axis.
.
EXAMPLE 2
What is the difference between the graphs of $latex f(x)=\cos(x)$ and the graphs of $latex g(x)=\cos(2x)$ and $latex h(x)=\cos( \frac{1}{2}x)$?
Solution
When we apply the transformation $latex g(x)=f(ax)$, where a is a constant, we produce a stretch or compression about the x-axis.
Therefore, we can look at the graph of the standard cosine function $latex f(x)=\cos(x)$ along with the other two functions:
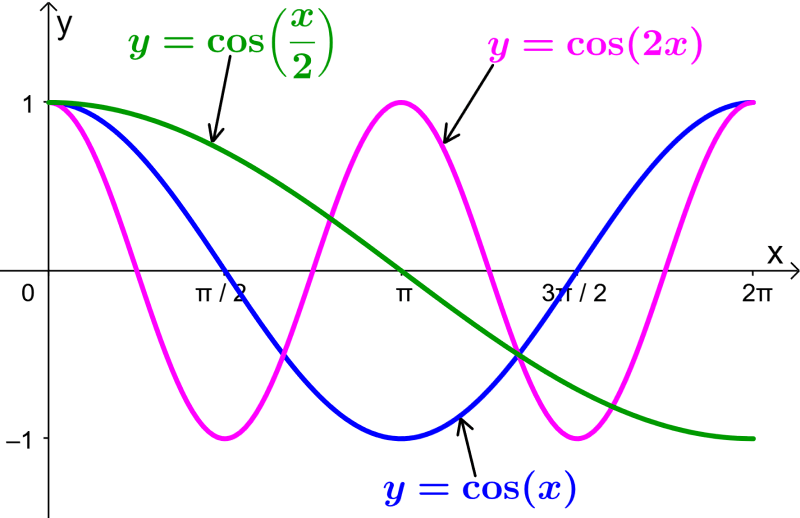
We see that the graph of $latex g(x)=\cos(2x)$ is halved, i.e. the stretch factor is $latex \frac{1}{a}=\frac{1}{2 }$.
In the case of the graph of $latex h(x)=\cos(\frac{1}{2}x)$, the function is stretched. The stretch factor is $latex \frac{1}{a}=\frac{1}{\frac{1}{2}}=2$.
EXAMPLE 3
Graph the functions $latex g(x)=2|x|$ and $latex h(x)=0.5|x|$.
Solution
In this case, we have the absolute value function, which in its base form, $latex f(x)=|x|$, has the following graph:
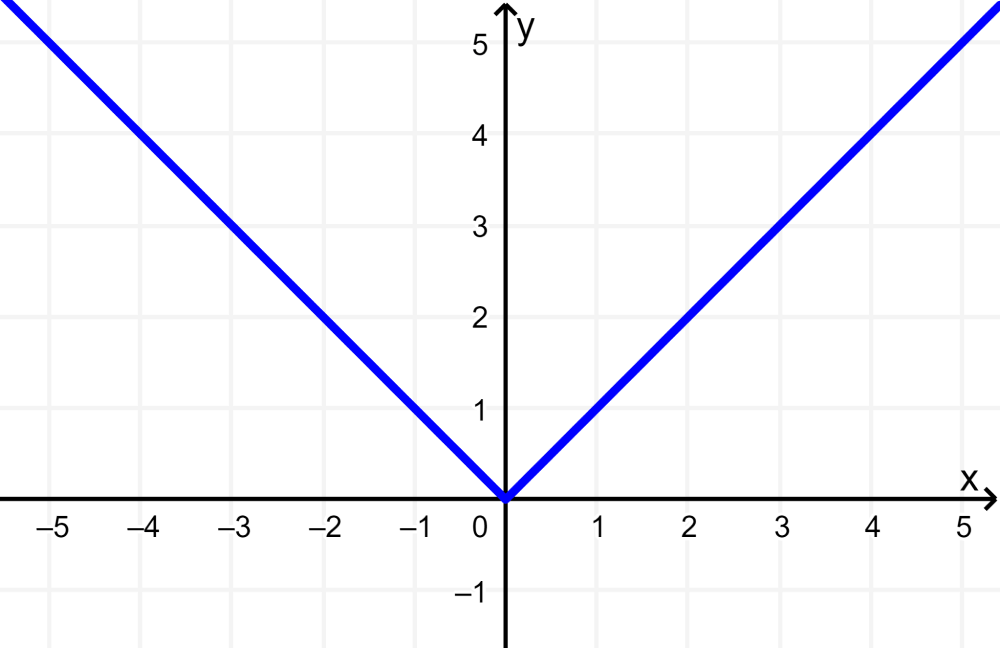
Now, the functions g and h are obtained by applying stretches with respect to the y-axis. That is, we have $latex g(x)=2f(x)$ and $latex h(x)=0.5f(x)$.
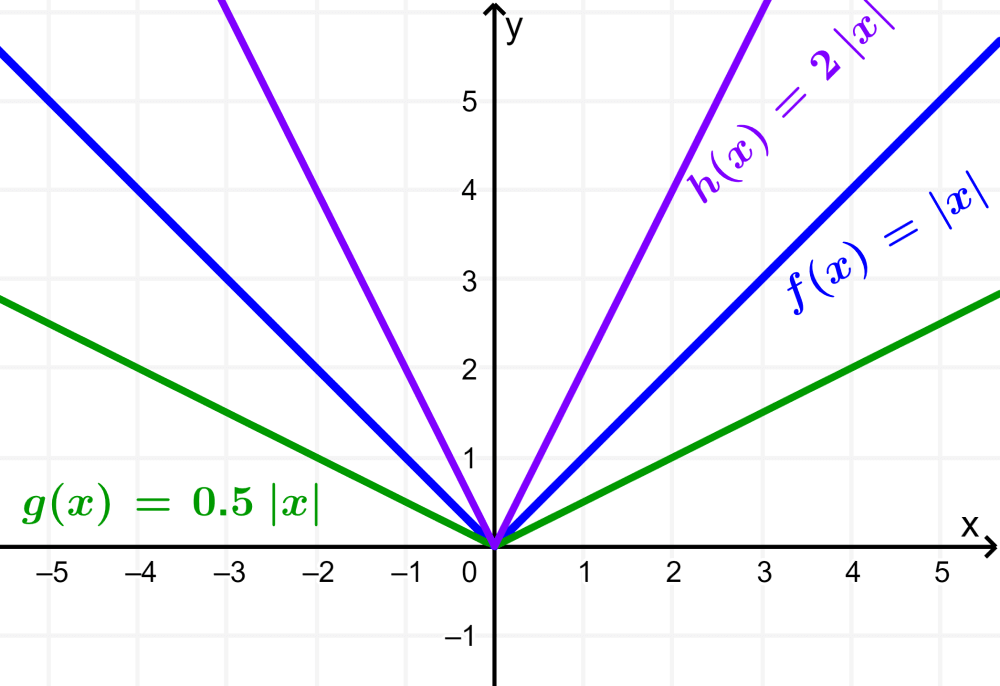
We see that the function h is stretched by a factor of 2 and the function g by a factor of 0.5 (equals a compression by half).
EXAMPLE 4
What changes do we need to make to the function $latex f(x)=3x^2+6x$ if we want to stretch it by a factor of 3 about the x-axis?
Solution
To stretch a function by a factor of 3 about the x-axis, we have to apply the transformation $latex g(x)=f(\frac{1}{3}x)$.
This means that we have to replace the variable x in f with $latex \frac{1}{3}x$. Therefore, we have:
$latex g(x)=f(\frac{1}{3}x)$
$latex g(x)=3(\frac{1}{3}x)^2+6(\frac{1}{3}x)$
$latex g(x)=3(\frac{1}{9})x^2+2x$
$latex g(x)=\frac{1}{3}x^2+2x$
Stretching and compression of functions – Practice problems
Apply everything you have learned about stretching and compressing functions to solve the following practice problems.
See also
Interested in learning more about function transformations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
