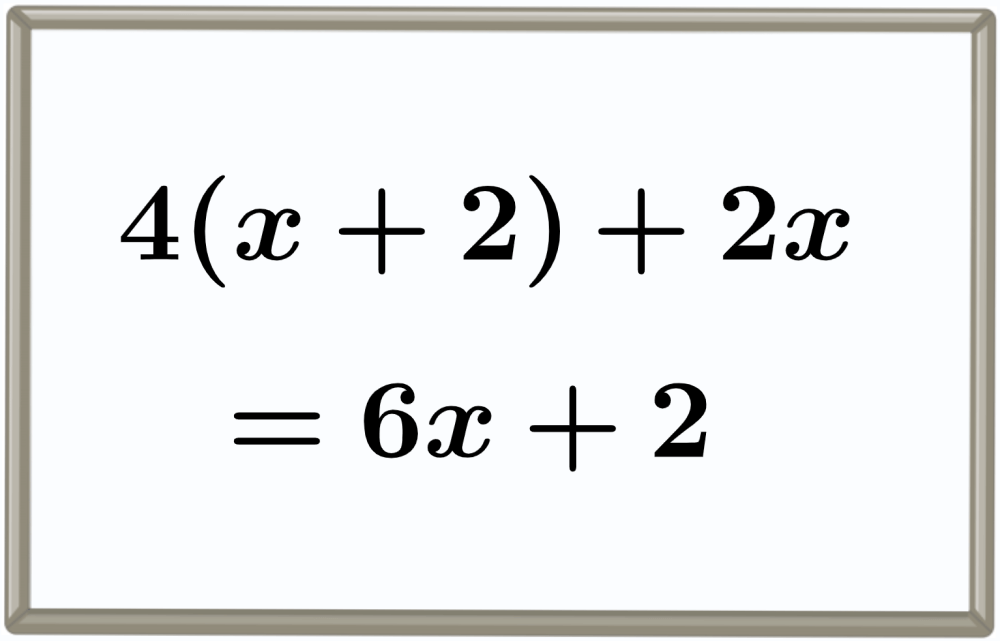Algebraic expressions can be simplified by using the distributive property to remove parentheses. Then, we combine like terms, that is, terms with the same variables and the same exponents. Finally, we add the constant terms.
In this article, we will look at a summary of simplifying algebraic expressions. In addition, we will explore several simplification examples with answers to fully master this topic.
Summary of simplification of algebraic expressions
The simplification of algebraic expressions allows us to obtain simpler expressions that can be manipulated with ease.
To simplify algebraic expressions, we can apply the distributive property to remove parentheses and other grouping signs, and we can combine like terms.
Distributive property
The distributive property tells us how to eliminate grouping signs by distributing the multiplication of a number to all the internal terms of the parentheses:
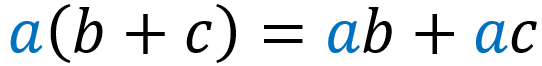
Combine like terms
Like terms are algebraic terms that have the same variables raised to the same power. For example, $latex 2{{x}^2}$ and $latex 3{{x}^2}$ are like terms since they have the same variable (x) raised to the same power (2). Similarly, the terms $latex 3x{{y}^3}$ and $latex 2x{{y}^3}$ are also like terms since they have the same variables raised to the same power.
10 Examples of simplification of algebraic expressions with answers
EXAMPLE 1
Simplify the algebraic expression:
$latex 2x+4+3x-5$
Solution
We have the variable x and we have constant terms. Therefore, we combine with terms with variables and combine the constant terms:
$latex 2x+4+3x-5$
$latex =(2x+3x)+(4-5)$
$latex =5x-1$
EXAMPLE 2
Simplify the algebraic expression:
$latex 3x+2(3x-2)+10$
Solution
We have a parenthesis so we start by using the distributive property to distribute the 2 and remove the parentheses:
$latex 3x+2(3x-2)+10$
$latex =3x+6x-4+10$
Now we combine like terms. We combine the variables and the constant terms:
$latex =(3x+6x)+(-4+10)$
$latex =9x+6$
EXAMPLE 3
Simplify the algebraic expression:
$latex 4x+2{{x}^2}+5-3x+4{{x}^2}+4$
Solution
In this case, we have the variable x with a power of 1 and with a power of 2, so we combine like terms separately for the power of 1 and for the power of 2. We also combine the constant terms separately:
$$4x+2{{x}^2}+5-3x+4{{x}^2}+4$$
$$=(2{{x}^2}+4{{x}^2})+(4x-3x)+(5+4)$$
$latex =6{{x}^2}+x+9$
EXAMPLE 4
Simplify the algebraic expression:
$latex 3x(2x+5)+10x-6+5{{x}^2}$
Solution
We start by applying the distributive property to remove the parentheses:
$$3x(2x+5)+10x-6+5{{x}^2}$$
$$=6{{x}^2}+15x+10x-6+5{{x}^2}$$
Now combine like terms. We combine terms with the variable x with different powers separately:
$$=(6{{x}^2}+5{{x}^2})+(15x+10x)-6$$
$latex =11{{x}^2}+25x-6$
EXAMPLE 5
Simplify the algebraic expression:
$latex 4x(y+3x)-3xy+5{{x}^2}+10-6x$
Solution
We start by removing the parentheses using the distributive property:
$latex 4x(y+3x)-3xy+5{{x}^2}+10-6x$
$$=4xy+12{{x}^2}-3xy+5{{x}^2}+10-6x$$
In this case, we have terms with both the x variable and the y variable. We have to combine terms that have the same variables raised to the same powers:
$$=(4xy-3xy)+(12{{x}^2}+5{{x}^2})+10-6x$$
$latex =xy+17{{x}^2}-6x+10$
EXAMPLE 6
Simplify the algebraic expression:
$$5(2x^2y+4x)+3x-2x(4xy-5)+12$$
Solution
We start by removing both parentheses using the distributive property:
$$5(2x^2y+4x)+3x-2x(4xy-5)+12$$
$$=10{{x}^2}y+20x+3x-8{{x}^2}y-10x+12$$
We have to combine the terms that have the same variables raised to the same power:
$$=(10{{x}^2}y-8{{x}^2}y)+(20x+3x-10x)+12$$
$latex =2{{x}^2}y+13x+12$
EXAMPLE 7
Simplify the algebraic expression:
$$-2x(3{{x}^2}+2x-1)+4x+2{{x}^2}+6-4{{x}^3}-10x+5$$
Solution
We start by removing the parentheses using the distributive property:
$$-2x(3{{x}^2}+2x-1)+4x+2{{x}^2}+6-4{{x}^3}-10x+5$$
$$=-6{{x}^3}-4{{x}^2}+2x+4x+2{{x}^2}+6-4{{x}^3}-10x+5$$
Here we have several terms with the variable x with different powers. We have to make sure to combine only the terms that have the same power:
$$=(-6{{x}^3}-4{{x}^3})+(-4{{x}^2}+2{{x}^2})+(2x+4x-10x)+(5+6)$$
$$=-10{{x}^3}-2{{x}^2}-4x+11$$
EXAMPLE 8
Simplify the algebraic expression:
$$-2a(3a+b)+4ab+2(a-2ab)+5a^2-10ab$$
Solution
Using the distributive property, we can remove the parentheses:
$$-2a(3a+b)+4ab+2(a-2ab)+5a^2-10ab$$
$$=-6a^2-2ab+4ab+2a-4ab+5a^2-10ab$$
Now, we combine like terms:
$$=-6a^2-2ab+4ab+2a-4ab+5a^2-10ab$$
$$=(-6a^2+5a^2)+(-2ab+4ab-4ab-10ab)+2a$$
$latex =-a^2-12ab+2a$
EXAMPLE 9
Find the simplest version of the expression:
$$ 5x(x-4)+4(2x-5)-10x^2+5x+17$$
Solution
Using the distributive property, we have the following:
$$ 5x(x-4)+4(2x-5)-10x^2+5x+17$$
$$ =5x^2-20x+8x-20-10x^2+5x+17$$
Combining like terms, we have:
$$ =5x^2-20x+8x-20-10x^2+5x+17$$
$$ =(5x^2-10x^2)+(20x+8x+5x)+(-20+17)$$
$$ =-5x^2+33x-3$$
EXAMPLE 10
Simplify the expression:
$$ 2x(x-2y)+5y(2x+5)+5x^2-10y+6(x^2-2xy)$$
Solution
We start by removing the parentheses using the distributive property:
$$ 2x(x-2y)+5y(2x+5)+5x^2-10y+6(x^2-2xy)$$
$$ =2x^2-4xy+10xy+25y+5x^2-10y+6x^2-12xy$$
Now, we combine like terms:
$$ =2x^2-4xy+10xy+25y+5x^2-10y+6x^2-12xy$$
$$ =(2x^2+5x^2+6x^2)+(-4xy+10xy-12xy)+(25y-10y)$$
$$ =13x^2-6xy+15y$$
→ Simplify Algebraic Expressions Calculator
Simplifying algebraic expressions – Practice problems
What is the simplified version of the following expression? $$y^2+2y(-y+2)+6x+y(y-3)-2x+2$$
Write the expression in the input box.
See also
Interested in learning more about algebraic expressions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
