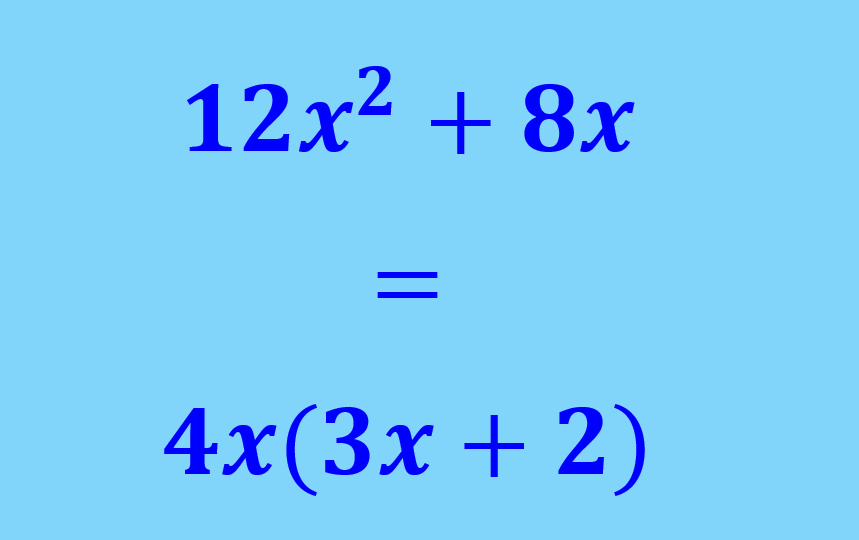Algebraic expressions can be factored by finding the common factor of all terms. After we find the common factor, we simply have to write the common factor followed by parentheses. Inside those parentheses, we write each term after it has been divided by the common factor.
In this article, we will look at a summary of the common factor and the reasoning used to extract factors from algebraic expressions. We will also explore several common factor examples with answers to master this concept.
Summary of common factors
Factoring an expression or a number means writing that expression or that number as a multiplication of factors. Therefore, factoring is the inverse of multiplication. When we multiply, we write:
$latex 5(x+y)=5x+5y$
But, if we factor, we write:
$latex 5x+5y=5(x+y)$
Here we factor $latex 5x+5y$ since we write it as the product $latex 5(x+y)$.
In the sum $latex 5x+5y$, 5 is a common factor of each term. The 5 is a factor of $latex 5x$ and also a factor of $latex 5y$.
Common factors – Examples with answers
The following common factor examples have their respective solution. You can try to solve the examples yourself before looking at the solution.
EXAMPLE 1
Factor the expression $latex 5x+5y$.
Solution
We can easily see that 5 is a factor in both the $latex 5x$ term and the $latex 5y$ term. Therefore, extracting the 5, we have:
$latex 5x+5y=5(x+y)$
EXAMPLE 2
Factor the expression $latex 8x-4y+12z$.
Solution
In this case, 4 is a common factor of all the terms. Therefore, we write the 4 to the left of the parentheses:
$$8x-4y+12z=4(2x-x+3z)$$
To verify the factorization, we can multiply and expand the parentheses. By doing this, we should get the original expression.
Note that the expression inside the parentheses should not have other common factors.
EXAMPLE 3
Factor the expression $latex -6a-9b-3c$.
Solution
In this expression, the common factor of all terms is -3. Therefore, we extract it from all the terms:
$$-6a-9b-3c=-3(2a+3b+c)$$
EXAMPLE 4
Extract the common factor of the expression $latex 6{{x}^2}+9x$.
Solution
In this case, we can see that the common factor of both terms is $latex 3x$:
$$6{{x}^2}+9x=3x(2x+3)$$
We can verify this by multiplying and expanding the expression on the right:
$$3x(2x+3)=6{{x}^2}+9x$$
EXAMPLE 5
Factor the polynomial $latex {{x}^6}+{{x}^5}+{{x}^4}+{{x}^3}$.
Solution
This polynomial is made up of terms that have the variable x raised to different powers. Thus, we find the smallest power in the terms and extract it. In this case, the smallest power is 3:
$${{x}^6}+{{x}^5}+{{x}^4}+{{x}^3}={{x}^3}({{x}^3}+{{x}^2}+{{x}^1}+1)$$
EXAMPLE 6
Factor the expression $latex 3{{x}^3}+6{{x}^2}+12x$.
Solution
In this case, we have common factors in both the variable and the coefficient. In the coefficients, the common factor is 3 and in the variables, the common factor is x:
$$3{{x}^3}+6{{x}^2}+12x=3x({{x}^2}+2x+4)$$
EXAMPLE 7
Factor the expression $latex 16{{x}^4}+32{{x}^3}-24{{x}^2}$.
Solution
The common factor of the variables is $latex {{x}^2}$ and the common factor of the coefficients is 8. Thus, we have:
$$16{{x}^4}+32{{x}^3}-24{{x}^2}=8{{x}^2}(2{{x}^2}+4x-3)$$
EXAMPLE 8
Factor the expression $latex {{x}^2}{{y}^3}{{z}^4}+{{x}^4}y{{z}^3}$.
Solution
Here we have three different variables. The common factor will contain the smallest power of each variable. Thus, the common factor is $latex {{x}^2}y{{z}^3}$. We write the expression extracting that common factor:
$${{x}^2}{{y}^3}{{z}^4}+{{x}^4}y{{z}^3}={{x}^2}y{{z}^3}({{y}^2}z+{{x}^2})$$
Common factor – Practice problems
The following common factor problems can be used to practice this concept. Factor the expressions given and select the correct answer. You will be able to verify your answer by clicking “Check”. If you have problems with these exercises, you can study the examples solved above.
See also
Interested in learning more about algebraic expressions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
