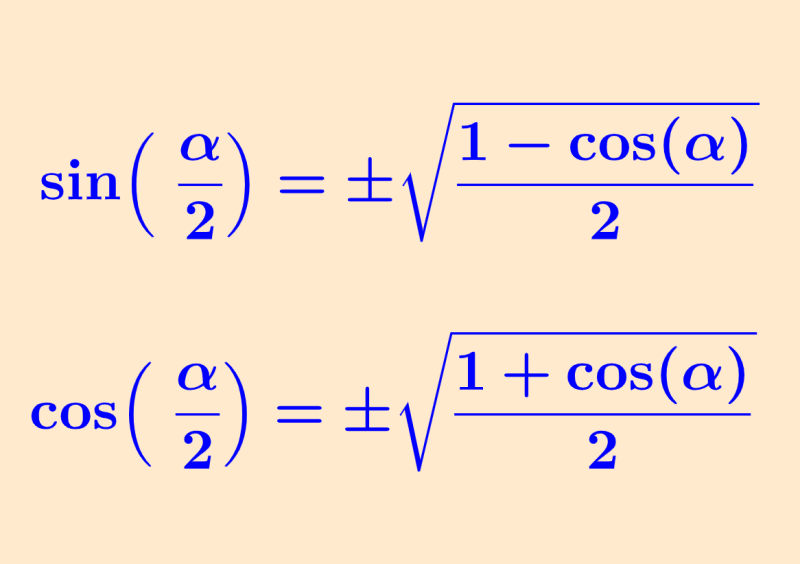Half-angle identities are trigonometric identities used to simplify trigonometric expressions and calculate the sine, cosine, or tangent of half-angles when we know the values of a given angle. These identities are obtained by using the double angle identities and performing a substitution.
Here, we will learn to derive the half-angle identities and apply them to solve some practice exercises.
What are the half-angle identities?
Half-angle identities are trigonometric identities that are used to calculate or simplify half-angle expressions, such as $latex \sin(\frac{\theta}{2})$. These identities can also be used to transform trigonometric expressions with exponents to one without exponents.
The half-angle identity of the sine is:
| $latex \sin(\frac{\theta}{2})=\pm \sqrt{\frac{1-\cos(\theta)}{2}}$ |
The half-angle identity of the cosine is:
| $latex \cos(\frac{\theta}{2})=\pm \sqrt{\frac{1+\cos(\theta)}{2}}$ |
The half-angle identity of the tangent is:
| $latex \tan(\frac{\theta}{2})=\frac{\sin(\theta)}{1+\cos(\theta)}$ $latex =\frac{1-\cos(\theta)}{\sin(\theta)}$ |
Proof of the half-angle identities
The mean angle identities can be derived using the double angle identities.
To derive the formula for the identity of half-angle of sines, we start with the double angle identity of cosines:
$latex \cos(2\theta)=1-2{{\sin}^2}(\theta)$
If we use the relation $latex \theta=\frac{\alpha}{2}$, we have $latex 2\theta=\alpha$. Substituting these expressions in the identity above, we have:
$latex \cos(\alpha)=1-2{{\sin}^2}(\frac{\alpha}{2})$
Now, we solve this expression for $latex \sin(\frac{\alpha}{2})$:
$latex \cos(\alpha)=1-2{{\sin}^2}(\frac{\alpha}{2})$
$latex 2{{\sin}^2}(\frac{\alpha}{2})=1-\cos(\alpha)$
$latex {{\sin}^2}(\frac{\alpha}{2})=\frac{1-\cos(\alpha)}{2}$
$latex \sin(\frac{\alpha}{2})=\pm\sqrt{\frac{1-\cos(\alpha)}{2}}$
The sign of $latex \sin(\frac{\alpha}{2})$ depends on the quadrant in which $latex \frac{\alpha}{2}$ is located. If $latex \frac{\alpha}{2}$ is in the first or second quadrant, the formula uses the positive sign, and if $latex \frac{\alpha}{2}$ is in the third or fourth quadrant, the formula uses the negative sign.
We use a similar process to find the half-cosine angle identity. Therefore, we start with the double-angle identity of the cosine in the following form:
$latex \cos(2\theta)=2{{\cos}^2}(\theta)-1$
After making the substitutions, we get:
$latex \cos(\alpha)=2{{\cos}^2}(\frac{\alpha}{2})-1$
Now, we solve for $latex \cos(\frac{\alpha}{2})$:
$latex \cos(\alpha)=2{{\cos}^2}(\frac{\alpha}{2})-1$
$latex 2{{\cos}^2}(\frac{\alpha}{2})=1+\cos(\alpha)$
$latex {{\cos}^2}(\frac{\alpha}{2})=\frac{1+\cos(\alpha)}{2}$
$latex \cos(\frac{\alpha}{2})=\pm\sqrt{\frac{1+\cos(\alpha)}{2}}$
In this case, if $latex \frac{\alpha}{2}$ is in the first or fourth quadrant, the formula uses the positive sign and if $latex \frac{\alpha}{2}$ is in the second or third quadrant, the formula uses the negative sign.
Half-angle identities – Example with answers
The following examples are solved using what you have learned about half-angle identities. Study and analyze these examples to understand the process used.
EXAMPLE 1
Use the half-angle identity of the sine to find the sine value of 15°.
Solution
We use the formula for the half-angle identity of the sine with the given value. Therefore, we have:
$latex \sin(\frac{\theta}{2})=\pm\sqrt{\frac{1-\cos(\theta)}{2}}$
$latex \sin(15^{\circ})=\pm\sqrt{\frac{1-\cos(30^{\circ} )}{2}}$
$latex =\pm\sqrt{\frac{1-0.866}{2}}$
$latex =0.259$
We use the positive value since 15° is in the first quadrant.
EXAMPLE 2
Determine the value of the cosine of 165° using the half-angle identity of the cosine.
Solution
To use the half-angle identity of cosine, we use the angle $latex \frac{\theta}{2} = 165$°. This means that we have $latex \theta = 330$°. Therefore, we use the formula with these values:
$latex \cos(\theta)=\pm\sqrt{\frac{1+\cos(\theta)}{2}}$
$latex \cos(165^{\circ})=\pm\sqrt{\frac{1+\cos(330^{\circ})}{2}}$
$latex =\pm\sqrt{\frac{1+0.866}{2}}$
$latex =-0.966$
We chose the negative value since the angle 165° is in the second quadrant.
EXAMPLE 3
Check that the identity $latex 2{{\sin}^2}(\frac{x}{2})+\cos(x)= 1$.
Solution
We can use the identity of the half-angle of sine to substitute and simplify the expression. By doing this, we have:
$latex 2{{\sin}^2}(\frac{x}{2})+\cos(x)$
$latex =2{{(\sqrt{\frac{1-\cos(x)}{2}})}^2}+\cos(x)$
$latex =2(\frac{1-\cos(x)}{2})+\cos(x)$
$latex =1-\cos(x)+\cos(x)$
$latex =1$
After simplifying, we see that the left side of the identity is equal to the right side, so the identity is true.
Half-angle identities – Practice problems
Solve the following practice problems using what you have learned about the half-angle identities of sine, cosine, and tangent. Select an answer and check it to see if you got the correct answer.
See also
Interested in learning more about trigonometric identities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
