A circle is the set of points that are equidistant from a fixed point. The fixed point is called the center and the distance from the center to a point on the circumference is called the radius. The equation of the circumference with center at the origin is found using the Pythagorean theorem on the Cartesian plane.
Here, we will derive this equation and apply it to solve some practice problems.
PRECALCULUS
Relevant for…
Finding the equation of the circumference centered at the origin.
PRECALCULUS
Relevant for…
Finding the equation of the circumference centered at the origin.
Determining the equation of a circumference with center at the origin
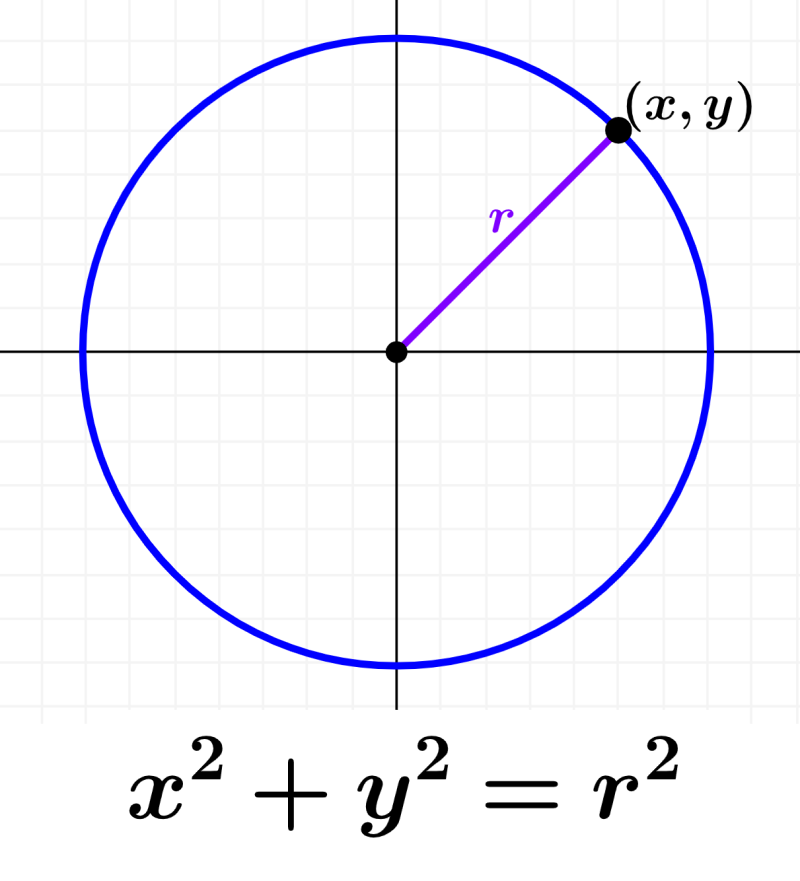
To find the equation of a circle centered at the origin, we can use the Cartesian plane in conjunction with the Pythagorean theorem. We draw a circumference as in the following diagram:
We see that the circumference has its center at the point (0, 0). We plot the point (x, y) that is located on the circumference. In addition, we also plot a right triangle that connects the center with the point (x, y).
The base of the triangle is equal to the x-coordinate of the point and the height is equal to the y-coordinate. We also note that the hypotenuse of the triangle is equal to the radius. Therefore, we can form the following equation:
| $latex {{x}^2}+{{y}^2}={{r}^2}$ |
This is the equation of the circumference centered at the origin, where r is the radius and (x, y) is any point that is located on the circumference.
Circumference center at the origin – Examples with answers
The following examples put into practice the use of the equation of the circumference centered at the origin. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Find the radius of the circumference represented by the equation $latex {{x}^2}+{{y}^2}=4$.
Solution
The following is the graph of this equation:
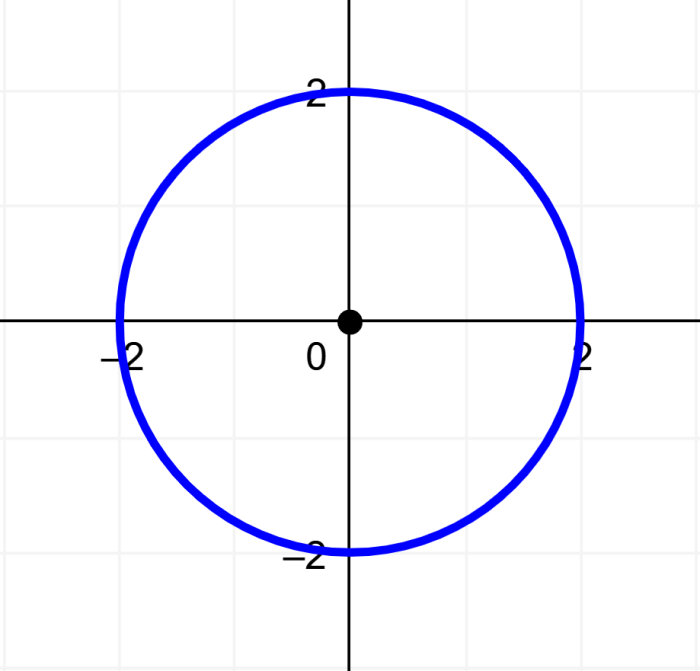
We know that a circle has the general equation $latex {{x}^2}+{{y}^2}={{r}^2}$. Comparing the general equation with the equation of the given circumference, we know that we have:
$latex {{r}^2}=4$
$latex r=2$
Therefore, the radius of the circumference is 2.
EXAMPLE 2
Find the equation of the circumference that has a radius of 5 and is centered at the origin.
Solution
We use the general equation for the circumference and plug in the value $latex r = 5$. Therefore, we have:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{x}^2}+{{y}^2}={{5}^2}$
$latex {{x}^2}+{{y}^2}=25$
EXAMPLE 3
Find the equation of the circumference that passes through the point (3, 5).
Solution
The point (3, 5) is located on the circumference. This means that we have the coordinates $latex x=3$ and $latex y=5$. Therefore, we use the equation of the circle with these coordinates to find the radius of the circle:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{3}^2}+{{5}^2}={{r}^2}$
$latex 9+25={{r}^2}$
$latex {{r}^2}=34$
Now, we plug this value into the general equation to obtain the equation for this circumference:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{x}^2}+{{y}^2}=34$
EXAMPLE 4
Determine whether the point (5, 6) is on the circumference $latex {{x}^2}+{{y}^2} = 61$.
Solution
We use the given equation with the coordinates of the point (5, 6). Therefore, we plug in the values $latex x=5$ and $latex y=6$ and check if the equation is true:
$latex {{x}^2}+{{y}^2}=61$
$latex {{5}^2}+{{6}^2}=61$
$latex 25+36=61$
$latex 61=61$
The equation is true. This means that the point (5, 6) is on the given circumference.
EXAMPLE 5
Determine if the point (7, 8) is on the circumference $latex {{x}^2}+{{y}^2}= 94$.
Solution
We plug the values $latex x=7$ and $latex y=8$ into the equation of the given circumference and check that the equation is true:
$latex {{x}^2}+{{y}^2}=94$
$latex {{7}^2}+{{8}^2}=94$
$latex 49+64=94$
$latex 113=94$
The equation is not true. This means that the point (7, 8) is not part of the given circumference.
Circumference with center at the origin – Practice problems
Use what you have learned about the equation for a circle with center at the origin to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about equations of a circumference? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
