The circumference is defined as the set of points that are equidistant from a fixed point called the center. The constant distance from the center to any point on the circumference is called the radius. It is possible to find the equation of the circumference if we know three points through which it passes. This requires plugging the known values into the general equation for the circumference and forming a system of three equations. The values of the missing constants can be found by solving the system of equations.
Here, we will look at some examples of the process used.
PRECALCULUS
Relevant for…
Finding the equation of the circumference using three points.
PRECALCULUS
Relevant for…
Finding the equation of the circumference using three points.
Determining the equation of a circumference using three points
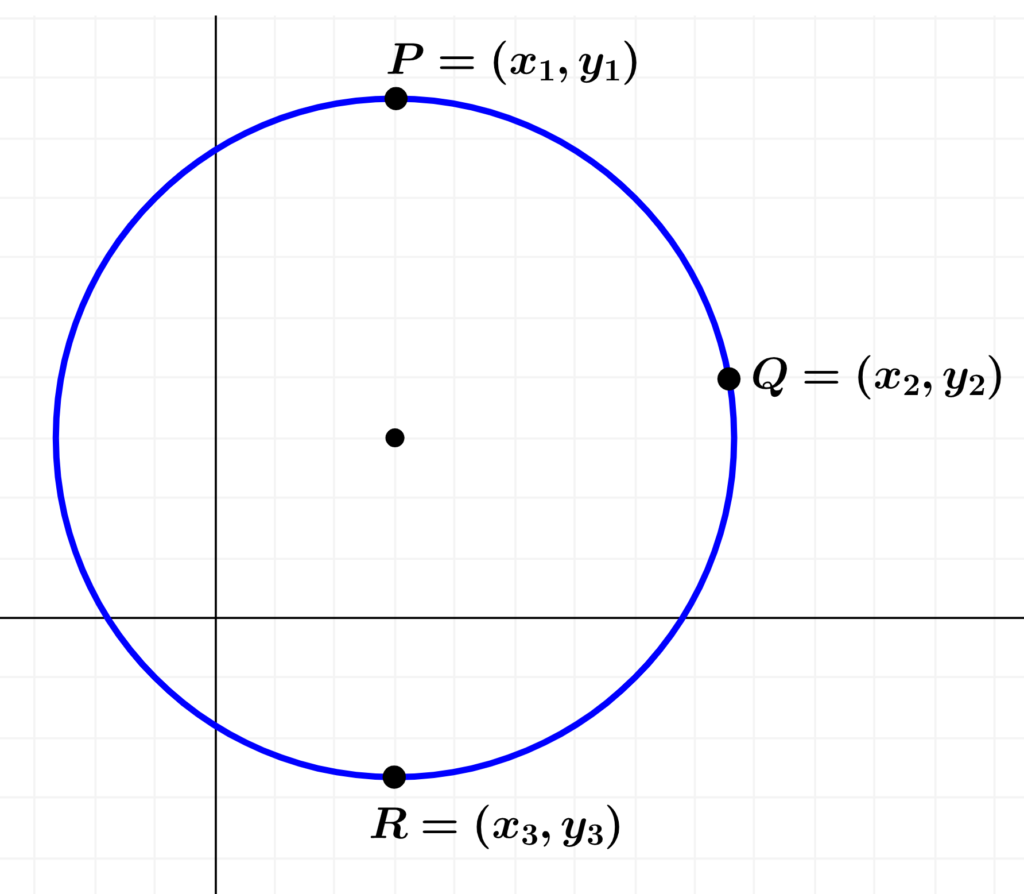
The equation of a circle can be found using the coordinates of three points that lie on the circle.
Suppose we have the points $latex P=(x_{1}, ~y_{1})$, $latex Q=(x_{2}, ~y_{2})$ and $latex R=(x_{3}, ~y_{3})$. We can observe this in the following diagram:
We can write the equation of a circle in the following general form:
$latex {{x}^2}+{{y}^2}+2ax+2by+c=0$ (1)
We can substitute the points $latex P=(x_{1}, ~y_{1})$, $latex Q=(x_{2}, ~y_{2})$ and $latex R=(x_{3}, ~y_{3})$ in the given equation to form different equations, one for each pair of coordinates. Therefore, we have:
$latex {{x_{1}}^2}+{{y_{1}}^2}+2ax_{1}+2by_{1}+c=0$ (2)
$latex {{x_{2}}^2}+{{y_{2}}^2}+2ax_{2}+2by_{2}+c=0$ (3)
$latex {{x_{3}}^2}+{{y_{3}}^2}+2ax_{3}+2by_{3}+c=0$ (4)
With equations (2), (3), and (4) we form a system of equations and find the values of the constants a, b and c. Then, we plug these values into equation (1) to find the equation for the required circumference.
Examples with answers of equation of a circumference using three points
The following exercises can be used to understand the process used to find the equation of a circle if we know the coordinates of three different points that are part of the circle.
EXAMPLE 1
Find the equation of the circle that passes through the points (1, 0), (-1, 0), and (0, 1).
Solution:
The equation of the circumference in its general form is $latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$. Using the coordinates of the given points, we can form the following equations:
$latex 1+2a+c=0$ (1)
$latex 1-2a+c=0$ (2)
$latex 1+2b+c=0$ (3)
We can subtract equation (2) from equation (1) to get $latex 4a = 0 $. This means that $latex a=0$.
We substitute the value $latex a=0$ in the equation (1), and we get $latex c=-1$. Finally, if we substitute the value $latex c = -1$ in equation (3), we have $latex b=0$.
If we substitute the values of a, b and c in the general equation, we have:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
$latex {{x}^2}+{{y}^2}+2(0)x+2(0)y+-1=0$
$latex {{x}^2}+{{y}^2}-1=0$
$latex {{x}^2}+{{y}^2}=1$
EXAMPLE 2
What is the equation of the circle that passes through the points (1, -6), (2, 1), and (5, 2)? Determine the length of its radius and the coordinates of its center.
Solution
The following is the equation of a circle in its general form:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
We use this equation with the coordinates of the given points to form a system of three equations.
Using the point (1, -6), we have:
$latex 1+36+2a-12b+c=0$
$latex 2a-12b+c=-37$ (1)
Using the point (2, 1), we have:
$latex 4+1+4a+2b+c=0$
$latex 4a+2b+c=-5$ (2)
Using the point (5, 2), we have:
$latex 25+4+10a+4b+c=0$
$latex 10a+4b+c=-29$ (3)
If we subtract equation (1) from (2), we have:
$latex 2a+14b=32$
⇒ $latex a+7b=16$ (4)
Now, if we subtract equation (1) from (3), we get:
$latex 8a+16b=8$
⇒ $latex a+2b=1$ (5)
Solving equations (4) and (5), we get $latex a=-5$ and $latex b=3$. Finally, using the values of a and b in equation (2), we obtain $latex c=9$.
If we substitute the values of a, b and c in the general equation, we have:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
$latex {{x}^2}+{{y}^2}+2(-5)x+2(3)y+9=0$
$latex {{x}^2}+{{y}^2}-10x+6x+9=0$
The coordinates of its center are $latex (-a, -b) = (5, -3)$ and the radius is $latex \sqrt{{{a}^2}+{{b}^2}-c}=\sqrt{25+9-9}=5$.
See also
Interested in learning more about equations of a circumference? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
