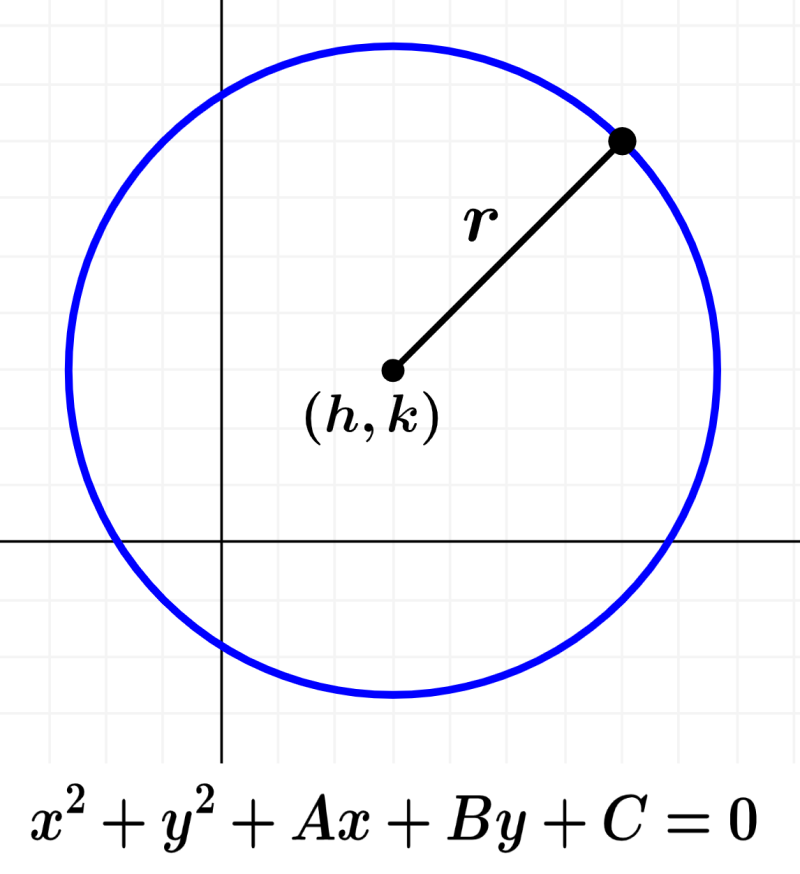
The circumference is formed by a set of points that are located at a constant distance from a fixed point. The constant distance is called the radius of the circumference and the fixed point is called the center. The equation of the circumference in its general form is obtained by expanding the equation used when the circumference has a center outside the origin.
Here, we will learn about the equation of the circumference in its general form and use it in some practice problems.
Determining the equation of a circumference in general form
Recall that a circumference with center at the point $latex (h, k)$ and with radius r can be written as the following equation:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
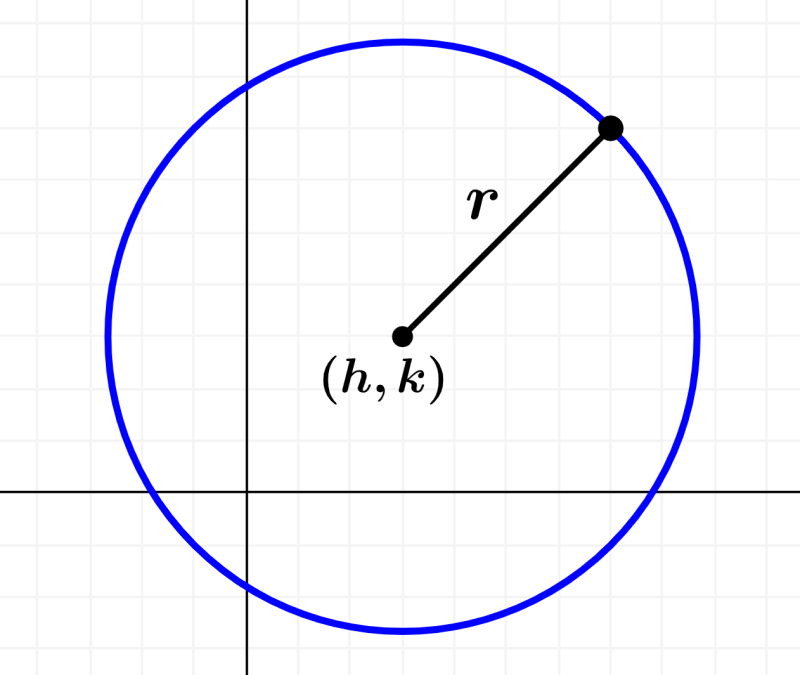
If we expand the squared parentheses, we have:
$${{x}^2}+{{y}^2}-2hx-2ky+{{h}^2}+{{k}^2}-{{r}^2}=0$$
If we make the substitutions $latex A=-2h$, $latex B=-2k$, $latex C={{h}^2}+{{k}^2}-{{r}^2}$ in the expanded equation, we have:
| $latex {{x}^2}+{{y}^2}+Ax+Bx+C=0$ |
This is the equation of the circumference in its general form. If we have an equation of a circle in this form, we can obtain the center and radius of the circle by using the following substitutions:
$latex A=-2h$ $latex B=-2k$ $latex C={{h}^2}+{{k}^2}-{{r}^2}$
Solving these expressions in terms of h, k and r, we have:
$latex h=-\frac{A}{2}$
$latex k=-\frac{B}{2}$
$latex {{r}^2}={{h}^2}+{{k}^2}-C$
$latex {{r}^2}={{(-\frac{A}{2})}^2}+{{(-\frac{B}{2})}^2}-C$
$latex {{r}^2}=\frac{{{A}^2}+{{B}^2}-4C}{4}$
In the original equation, we know that the center of the circumference is the point $latex (h, k)$. This means that the center of the circumference in its general form is $latex (-\frac{A}{2}, -\frac{B}{2})$ and the radius is $latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
Circumference in general form – Examples with answers
The following examples show the process used to solve the equation of the circumference problems in general form. It is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
If we have the circumference $latex {{x}^2}+{{y}^2} -2x + 4y-4 = 0$, what is its center and its radius?
Solution
The following is the graph of this equation:
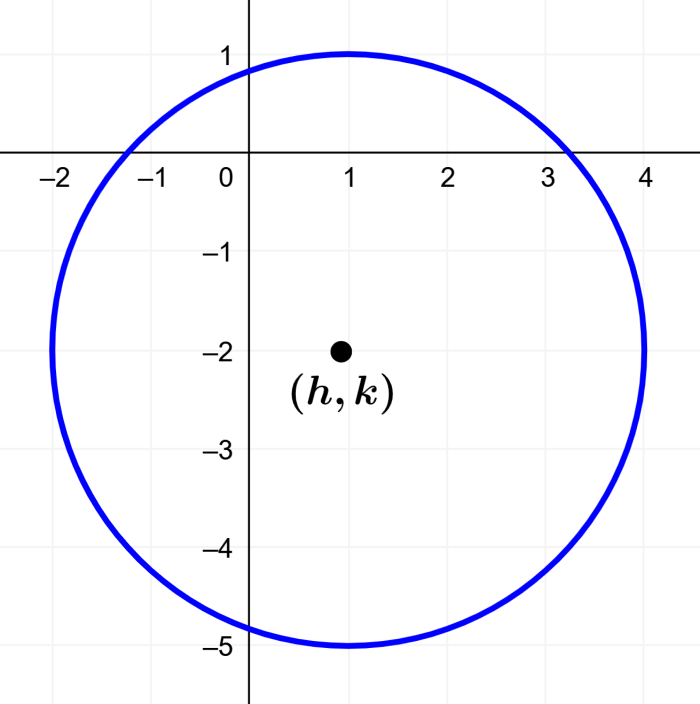
Using the derived expressions above, we know that the center of a circle in its general form is given by:
$latex (-\frac{A}{2}, -\frac{B}{2})=(-\frac{-2}{2}, -\frac{4}{2})=(1, -2)$
and the radius is given by:
$latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
$latex =\sqrt{\frac{{{(-2)}^2}+{{4}^2}-4(-4)}{4}}$
$latex =\sqrt{\frac{4+16+16}{4}}$
$latex =\sqrt{\frac{36}{4}}$
$latex =\frac{6}{2}=3$
Therefore, the radius of the circumference is 3 and the center is the point (1, -2).
EXAMPLE 2
Find the center and radius of the circumference $latex {{x}^2} + {{y}^2} + 6x-2y + 3 = 0$.
Solution
We use the given expressions and identify the respective parameters. Therefore, the center of a circle in its general form is given by:
$latex (-\frac{A}{2}, -\frac{B}{2})=(-\frac{6}{2}, -\frac{-2}{2})=(-3, 1)$
and the radius is given by:
$latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
$latex =\sqrt{\frac{{{6}^2}+{{(-2)}^2}-4(3)}{4}}$
$latex =\sqrt{\frac{36+4-12}{4}}$
$latex =\sqrt{\frac{28}{4}}$
$latex =\sqrt{7}$
Therefore, the radius of the circle is $latex \sqrt {7}$ and the center is the point (-3, 1).
EXAMPLE 3
Find the equation of the circumference in its general form that has a radius of 2 and a center at (2, 2).
Solution
To find the equation of the circumference in its general form, we have to find the value of the constants A, B and C. Therefore, we are going to use the expressions given above remembering that the center of the circumference is (h, k):
$latex A=-2h=-2(2)=-4$
$latex B=-2k=-2(2)=-4$
$latex C={{h}^2}+{{k}^2}-{{r}^2}$
$latex C={{2}^2}+{{2}^2}-{{2}^2}$
$latex C=4+4-4=4$
Now, we form the equation of the circumference with the found values:
$latex {{x}^2}+{{y}^2}+Ax+By+C=0$
$latex {{x}^2}+{{y}^2}-4x-4y+4=0$
EXAMPLE 4
What is the equation of the circle that has a radius of 4 and a center at (3, -2)?
Solution
We find the values of the constants A, B and C using the expressions given above:
$latex A=-2h=-2(3)=-6$
$latex B=-2k=-2(-2)=4$
$latex C={{h}^2}+{{k}^2}-{{r}^2}$
$latex C={{3}^2}+{{(-2)}^2}-{{4}^2}$
$latex C=9+4-16=-3$
Now, we form the equation of the circumference with the found values:
$latex {{x}^2}+{{y}^2}+Ax+By+C=0$
$latex {{x}^2}+{{y}^2}-6x+4y-3=0$
Circumference in general form – Practice problems
Solve the following problems using what you have learned about equations of the circumference in general form. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about equations of a circumference? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
