Velocity and speed are concepts that allow us to study the motion of objects in physics. The main difference between these two concepts is that speed is a scalar quantity and velocity is a vector quantity.
In this article, we will look at detailed descriptions of speed and velocity. Then, we will learn about their main differences along with a few examples of each.
What is speed in physics?
In the most fundamental sense, speed refers to how fast an object moves. In physics, it is defined as the rate at which an object travels a distance.
Speed is a scalar quantity, which means that it has only magnitude and no specific direction.
Factors affecting speed
Two key components determine speed: distance and time.
Time: Speed is inversely proportional to time. The longer the time taken, the slower the speed, and vice versa, assuming that the distance traveled is constant.
Distance: Speed is directly proportional to distance. The greater the distance traveled in a given time, the greater the speed, and vice versa.
EXAMPLES OF SPEED
Travel by car
If a car travels 100 km in 2 hours, the average speed of the car is 50 km per hour. This is calculated by dividing the total distance (160 km) by the total time (2 hours).
However, this tells us nothing about the direction of motion or any change in its speed during travel.
An athlete
A sprinter running 100 meters is concerned about how fast he can run. He wants to cover the set distance in the shortest possible time.
Calculating speed
The basic formula for speed is $latex v = \frac{s}{t}$, where “$latex s$” represents distance and “$latex t$” represents time. This formula gives us the average speed because, in the real world, speed can change often.
What is velocity in physics?
Velocity, like speed, is a measure of the rate of change of an object’s position. However, it is a vector quantity, meaning that it has both magnitude (speed) and direction.
Velocity can be thought of as the speed with which an object moves in a given direction.
Factors affecting velocity
The two main factors influencing velocity are displacement and time, along with consideration of direction.
Time: Velocity is inversely proportional to time. The longer the time required for a given displacement, the slower the velocity, and vice versa.
Displacement: Displacement is different from distance. It is the shortest path between the initial and final positions of an object, and depends on the direction. The greater the displacement in a given time, the greater the velocity, and vice versa.
Direction: Direction affects velocity. A change in direction, even with constant speed, will cause a change in velocity.
EXAMPLES OF VELOCITY
Travel by car
If a car travels 100 kilometers eastward in 2 hours, the average speed of the car is 50 kilometers per hour eastward. This tells us not only how fast the car is traveling, but also the direction in which it is moving.
An athlete
Sprinters may have a high speed, but if they complete a lap and return to the starting point, their velocity is zero. This is because their overall displacement is zero, they finished where they started, and the velocity takes direction into account.
Calculating velocity
The basic formula for velocity is $latex v = \frac{\Delta d}{\delta t}$, where “$latex d$” represents displacement and “$latex t$” represents the change in time. Note that the displacement implies both the change in position and the direction of motion.
Differences between speed and velocity
Although both speed and velocity refer to how fast an object changes position, there are crucial differences between the two concepts:
Scalar vs vector: Speed is a scalar quantity, that is, it has only magnitude and no direction. On the other hand, velocity is a vector quantity that has magnitude and direction.
Distance vs displacement: Speed is based on the total distance an object travels, regardless of direction. Velocity, on the other hand, is based on displacement, which is the shortest path from the starting point to the final point in a specific direction.
Change of direction: A change of direction does not affect speed. However, a change of direction, even without a change of speed, causes a change of velocity because the velocity depends on the direction.
| Speed | Velocity | |
|---|---|---|
| Definition | The rate at which an object covers distance, regardless of direction. | The rate at which an object changes its position in a specific direction. |
| Quantity | Scalar | Vector |
| Formula | $latex v=\frac{\text{distance}}{\text{time}}$ | $latex v=\frac{\text{displacement}}{\text{time}}$ |
| Direction | Direction does not affect speed. | Changes in direction result in changes in speed. |
| Zero | The speed is zero only when the object is stationary. | It can be zero even when there is motion when the net displacement is zero. |
| Units | Meters per second (m/s), kilometers per hour (km/h), miles per hour (mph), etc. | Same as speed, but with direction: 60 km/h north. |
Examples demonstrating the differences
Consider a cyclist who goes for a ride around the city and returns to his starting point. The cyclist’s speed represents the total distance he has traveled during the entire ride, while his velocity would be zero because the total displacement (from the final point to the starting point) is zero.
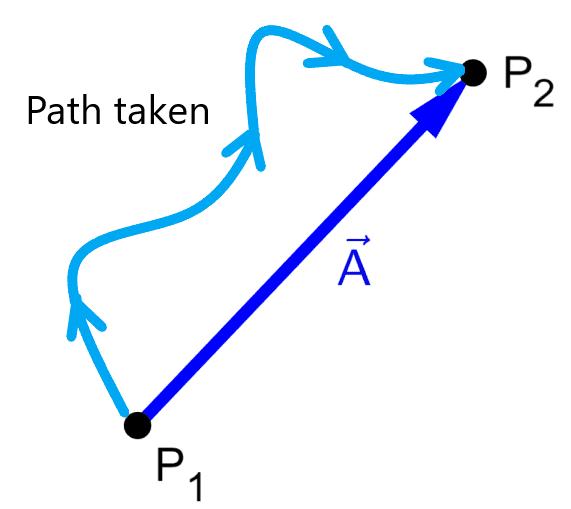
Now, let’s consider a car taking the path shown in the following diagram. The speed is calculated by considering the distance of the path taken, while the velocity is calculated using the displacement vector $latex \vec{A}$:
Practical applications of speed and velocity
Both speed and velocity have various applications in our daily lives. For example, understanding speed is crucial when driving: respecting speed limits, calculating travel time, and ensuring safety on the road.
Sports
In sports, athletes, especially runners or swimmers, often focus on their speed to improve their performance.
Navigation
Velocity is critical when steering is important. Pilots and boat captains need to know the speed to sail correctly, taking into account both speed and direction.
Space exploration
Understanding speed is essential for launching, navigating, and landing spacecraft. When scientists calculate the trajectory of a spacecraft, they must take into account both its speed and its direction, i.e., its velocity.
Mechanical and civil engineering
In engineering, knowing the speed of a machine’s moving parts can help predict their performance and wear. Understanding the velocity of fluids in pipes can help design efficient and safe plumbing and sewage systems.
Computer science
In computer graphics and game design, speed is used to create realistic movements of characters and objects.
Drones
In the growing field of drone technology, understanding speed is crucial for programming drones that fly accurately and efficiently.
Transportation technologies
The principles of speed and velocity have been central to the development of transportation technologies, from the design of high-speed trains to the development of autonomous vehicles.
Telecommunications
Speed and velocity are crucial in telecommunications, especially in data transmission, where speed and direction of signal propagation are key to efficient and effective communication systems.
See also
Interested in learning more about motion? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
