Both distance and displacement are fundamental concepts in the study of motion in physics. The main difference between these two concepts is that distance is a scalar quantity and displacement is a vector quantity.
In this article, we will learn about displacement and distance in detail. Then, we will look at some examples of these concepts.
PHYSICS
Relevant for…
Learning about the differences between distance and displacement.
PHYSICS
Relevant for…
Learning about the differences between distance and displacement.
What is distance in physics?
In physics, distance is a scalar quantity representing the total path length between two points. In simpler terms, it is the total motion of an object, regardless of its direction.
In everyday language, distance represents how far an object has traveled, regardless of the path it took to reach its endpoint.
Since distance is a scalar quantity, it has only magnitude and no direction. For example, if you walk 5 kilometers east and then 5 kilometers back west, the total distance traveled will be 10 kilometers.
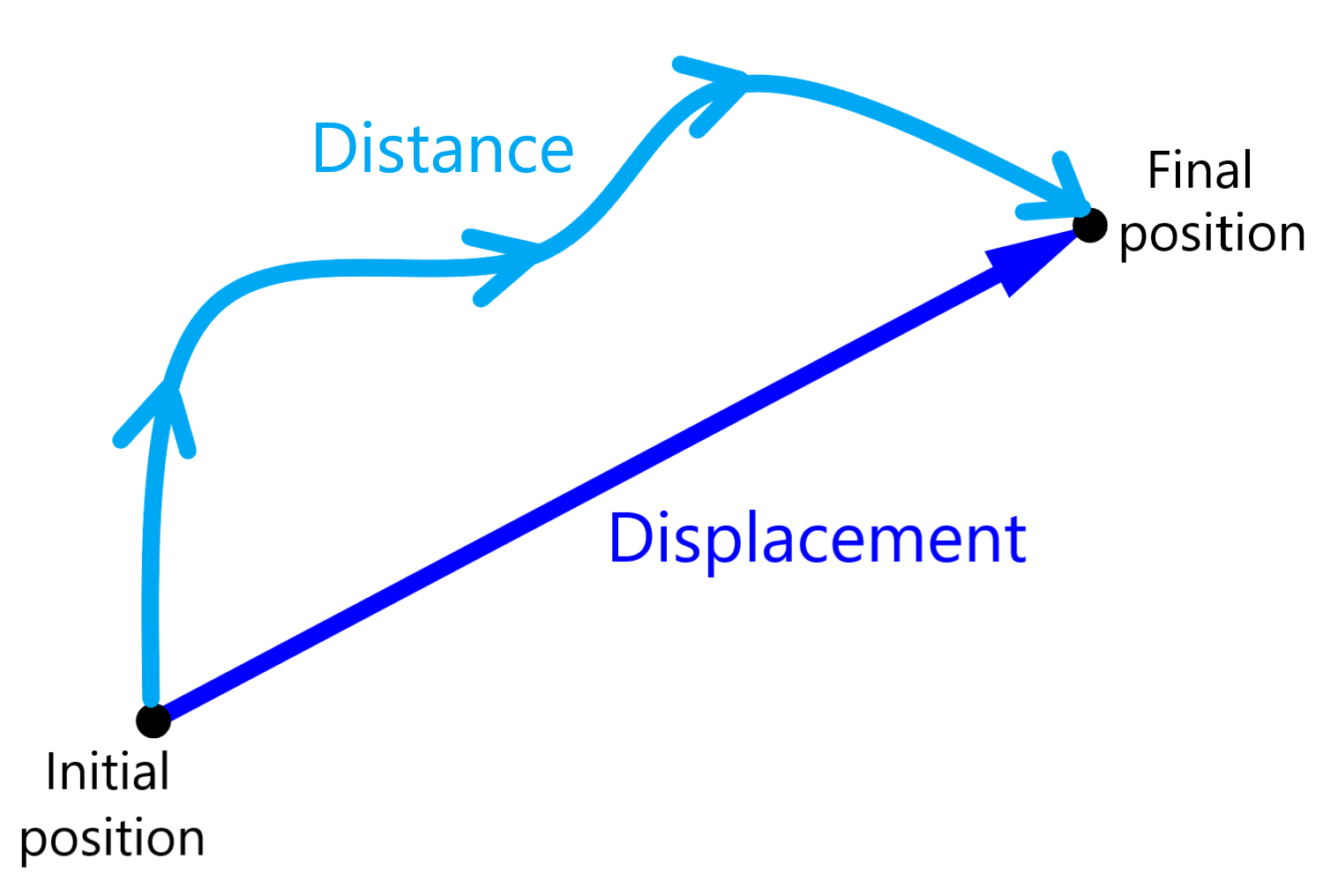
In the following diagram, although the starting point and the arrival point are the same, the distance is a positive quantity, since the object moved:
Distance is measured in standard units of length, such as meters in the International System of Units (SI). Other units, such as kilometers, centimeters, miles and feet, are also commonly used, depending on the context.
EXAMPLES OF DISTANCE
A walk through the city
Imagine you start at your hotel, walk 2 kilometers to a museum, then 3 kilometers to a restaurant, and finally 1 kilometer to a park. The total distance is the sum of all these individual distances, which is 6 kilometers. This is regardless of the direction in which you walked.
Track runner
If a runner completes four laps on a 400-meter track, the total distance he has run is 1,600 meters or 1.6 kilometers, regardless of the direction of his run.
Distance calculation
Calculating the distance is simple when the path of motion is a straight line. It is simply the length of the path traveled. However, when the path is not straight, the distance is calculated by adding up all the individual distances.
In the case of constant velocity or speed, the distance can be calculated by the formula $latex \text{distance} = \text{speed} \times \text{time}$. For example, if a car travels at a constant speed of 60 kilometers per hour for 2 hours, the distance traveled by the car would be 120 kilometers.
Note that this formula assumes a constant speed, which is not always the case in the real world due to factors such as traffic, acceleration, and deceleration. When speed varies, more complex models and calculations may be necessary to accurately calculate distance.
What is displacement in physics?
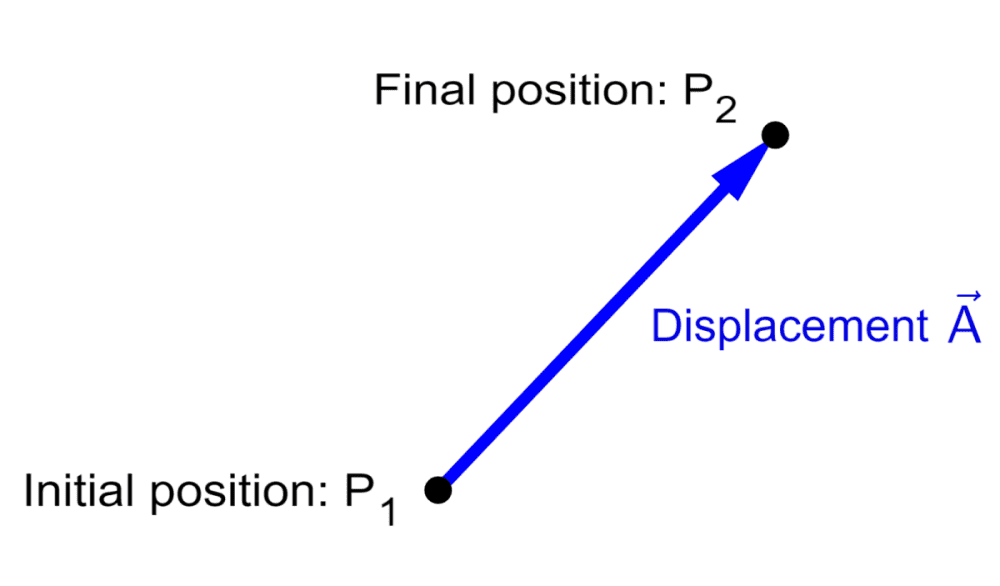
Displacement is a vector quantity that measures the interval between two points. Displacement defines the shortest distance from the initial to the final position of a point, often referred to as the “straight line distance”, and specifies the direction of that line.
If you walk 5 kilometers east and then 5 kilometers west, your displacement is zero, because your initial and final positions coincide. In physics, displacement is represented as a vector with an arrow.
Like distance, displacement is also measured in standard units of length such as meters in the International System of Units (SI), although other units such as kilometers, centimeters, miles or feet may be used.
The displacement is represented by an arrow that goes from the initial position to the final position of the object:
EXAMPLES OF DISPLACEMENT
A walk through the city
If you start at your hotel, walk 2 kilometers to a museum, then 3 kilometers to a restaurant, and finally 1 kilometer to a park, your total distance traveled is 6 kilometers.
However, your displacement would be the straight line distance from your hotel (starting point) to the park (ending point), taking into account the direction. If the park is 4 kilometers east of the hotel, then your displacement is 4 kilometers east.
Track runner
In the case of the runner on a track, if the runner completes four laps on a 400-meter track and stops where he started, his displacement is zero because his starting and ending points are the same.
Displacement calculation
Displacement is calculated as the vector difference between the initial and final positions of the point. When the motion is in a straight line, it can be calculated by subtracting the initial position from the final position.
In the case of a straight-line motion with constant velocity, the displacement can be calculated by the formula $latex \text{displacement} = \text{velocity} \times \text{time}$. In this formula, velocity is a vector quantity that incorporates both speed and direction.
For example, if a car moves at a constant speed of 50 kilometers per hour eastward for 3 hours, the displacement of the car would be 150 kilometers eastward.
When the velocity varies, this is more complex and often requires calculus or graphical methods to find the displacement accurately.
Differences between distance and displacement
Distance and displacement are fundamentally different in several respects:
Scalar vs Vector: Distance is a scalar quantity, that is, it has only magnitude and no direction. Displacement, on the other hand, is a vector magnitude, that is, it has magnitude and direction.
Total Path vs Direct Path: Distance is the total length of the path traveled by an object, regardless of direction. In contrast, displacement is the shortest straight-line distance between the start and end positions of an object, with the specified direction.
Always positive vs positive/negative: Distance is always a positive quantity (or zero if there is no motion), reflecting the total path traveled. Displacement, however, can be positive, negative, or zero, depending on the direction of motion.
We can observe the main differences between distance and displacement in the following table:
| Distance | Displacement | |
|---|---|---|
| Scalar or vector | Scalar | Vector |
| Direction | No | Yes |
| Finds | Total length of the journey | Direct length from the start point to the end |
| Can be negative | No | Yes |
In the following diagram, the “Path taken” represents the distance traveled by an object, while the vector $latex \vec{A}$ represents the displacement:
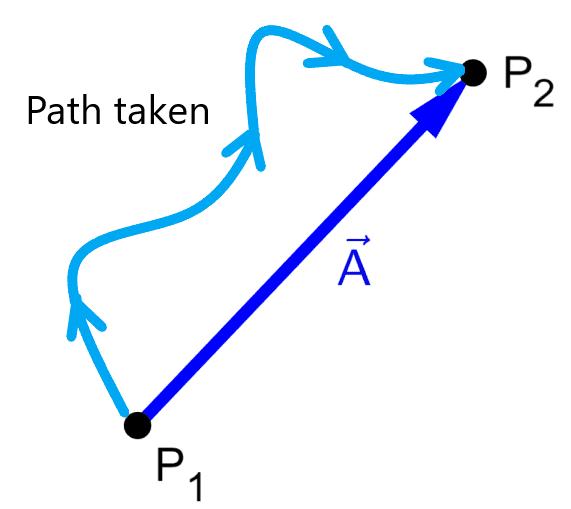
In the following diagram, the final point of the object is equal to the starting point, so the displacement is equal to zero.
Practical applications of distance and displacement
Navigation and transportation
Distance is used to measure the duration of a trip or other useful measures. For example, the distance traveled by a car can be used to calculate fuel consumption. On the other hand, displacement is essential for determining the most direct route from one place to another, which is important in air and sea navigation.
Sports and games
In sports, distance and displacement are crucial for measuring performance and scoring. For example, the distance traveled by a player during a football match or the displacement of a golf ball from the tee to the hole.
Physics and Engineering
Distance and displacement are fundamental concepts in physics, influencing many subfields such as mechanics, waves, and field theory. They are also crucial in engineering disciplines, such as mechanical engineering, for analyzing the motion of machine parts.
Computational modeling and simulation
In computer graphics and game development, displacement is essential to create the realistic movement of characters and objects. In scientific simulations, such as predicting the path of a hurricane, both distance and displacement are critical.
Geology and seismology
Displacement is a vital concept in the study of plate tectonics and earthquake prediction. Soil displacement can indicate the magnitude of an earthquake and help design structures capable of withstanding such natural catastrophes.
Astronomy and Space Sciences
Distance and displacement are essential for tracking the motion of celestial bodies and navigating space missions. For example, astronomers use light-years as a unit of distance to describe the vast expanses of space.
See also
Interested in learning more about motion? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
