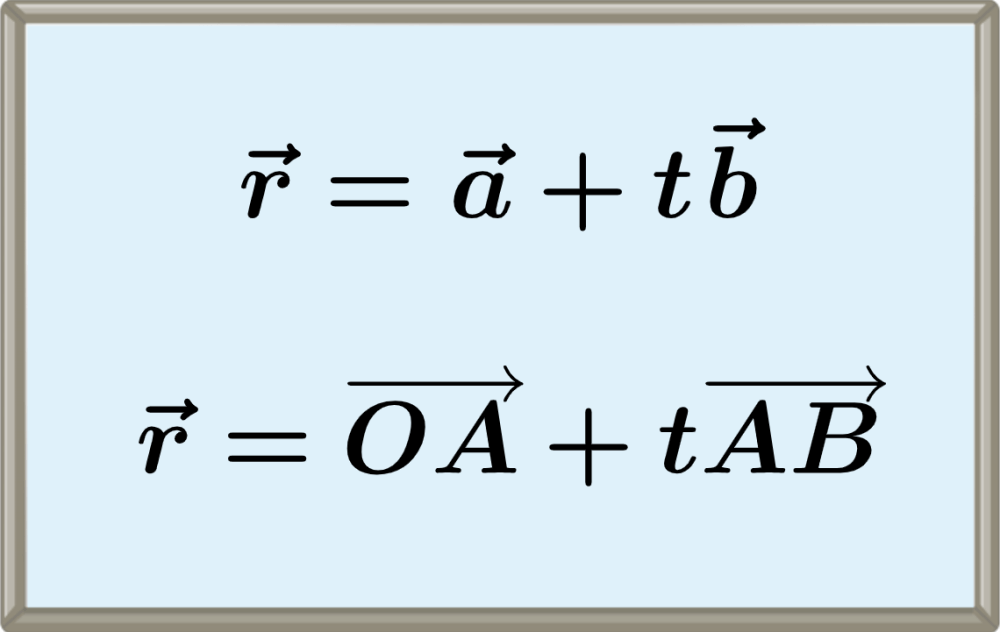The vector equation of a line is used to describe the position of each point on a line in terms of a single parameter, usually denoted t. We can find the vector equation of a line if we know two points on the line, or a point and a direction.
In this article, we will learn how to find the vector equation of a line using both cases mentioned above. Then, we will look some examples where we will apply these cases.
How to find the vector equation of a line?
There are two main methods we can use to find the vector equation of a line depending on the information we have available:
- A point on a line and the direction of the line
- Two points on the line
First case
Given a point $latex A $ and a direction $latex \vec{u}$, we can find the position vector $latex \vec{r}=\overrightarrow{OP}$ of a general point $latex P$ on the line:
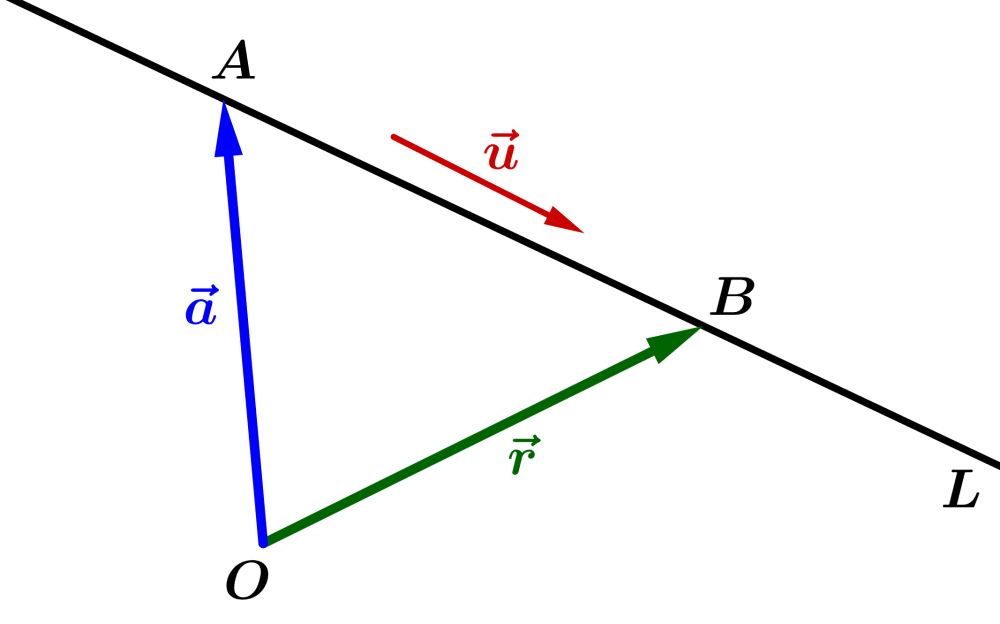
Using vector addition, we can see that:
$latex \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}$
Here we have $latex \vec{a}=\overrightarrow{OA}$ and since $latex \overrightarrow{AP}$ is parallel to $latex =\vec{u}$, we can write:
$latex \vec{r}=\vec{a}+t~\vec{u}$
where $latex t$ is a parameter or scalar quantity. In this equation, different values of $latex t$ give us all the points on the line.
Second case
When we know two points $latex A$ and $latex B$ on the line, we can express the vector equation of the line in terms of the position vectors of the points.
Similar to the previous case, we have $latex \vec{a}=\overrightarrow{OA}$. Also, in this case, $latex \overrightarrow{AB}$ is parallel to the line, so $latex \vec{u}=\overrightarrow{AB}$ and we have:
$latex \vec{r}=\overrightarrow{OA}+t~\overrightarrow{AB}$
Solved examples of vector equation of a line
EXAMPLE 1
Given two points A(1, 2, 3) and B(4, 6, 9), find the vector equation of the line through these points.
Solution
To find the vector equation of a line, we have to start by finding the position vector of a point on the line ($latex \overrightarrow{OA}$) and the direction vector ($latex \overrightarrow{AB}$) of the line.
Since point $latex A$ has coordinates $latex (1,~ 2,~ 3)$, and point $latex B$ has coordinates $latex (4, ~6, ~9)$, its position vector will be :
$$\overrightarrow{OA} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$
$$\overrightarrow{OB} = \begin{pmatrix} 4 \\ 6 \\ 9 \end{pmatrix}$$
Now we have to find the direction vector ($latex \vec{AB}$) of the line. This can be found by taking the difference between the position vectors of points A and B:
$$\overrightarrow{AB} = \overrightarrow{OB}~ – ~\overrightarrow{OA}$$
$$\overrightarrow{AB} = \begin{pmatrix} 4 \\ 6 \\ 9 \end{pmatrix} – \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 3 \\ 4 \\ 6 \end{pmatrix}$$
Now, we can write the vector equation of the line:
$latex \vec{r} = \overrightarrow{OA} + t~\overrightarrow{AB}$
$$\vec{r} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \begin{pmatrix} 3 \\ 4 \\ 6 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 1+3t \\ 2+4t \\ 3+6t \end{pmatrix}$$
EXAMPLE 2
Given a point $latex C(2,~ -1,~ 4)$ on the line and the direction vector of the line $latex \vec{d} = 4\hat{i}, ~5\hat{j}, ~-2\hat{k}$, find the vector equation of the line.
Solution
In this case, we know the position vector of point C on the line and the direction vector ($latex \vec{d}$) of the line.
The position vector of point C with coordinates $latex (2,~ -1, ~4)$ is:
$$\overrightarrow{OC} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix}$$
The direction vector of the line is given by:
$$\vec{d} = \begin{pmatrix} 4 \\ 5 \\ -2 \end{pmatrix}$$
Now, we can write the vector equation of the line:
$latex \vec{r} = \overrightarrow{OC}+ t~\vec{d}$
$$\vec{r} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + t \begin{pmatrix} 4 \\ 5 \\ -2 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 2+4t \\ -1+5t \\ 4-2t \end{pmatrix}$$
EXAMPLE 3
Given a point $latex A(5,~ -2,~ 3)$ on the line and the direction vector of the line $latex \vec{e} = 2\hat{i} -3\hat{j} +1 \hat{k}$, find the vector equation of the line.
Solution
Similar to the previous example, we know the position vector of point R on the line and the direction vector ($latex \vec{e}$) of the line.
The position vector of point A with coordinates $latex (5,~ -2, ~3)$ is:
$$\overrightarrow{OA} = \begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix}$$
In addition, we have that the direction vector of the line is:
$$\vec{e} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
Then, we can write the vector equation of the line using this information:
$latex \vec{r} = \overrightarrow{OA}+ t~\vec{e}$
$$\vec{r} = \begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix} + t \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 5+2t \\ -2-3t \\ 3+t \end{pmatrix}$$
EXAMPLE 4
Find the vector equation of the line through the two points P(-1, 3, 2) and Q(3, 7, -1).
Solution
We need to start by finding the position vectors ($latex \overrightarrow{OP}$) and ($latex \overrightarrow{OQ}$).
Since point $latex P$ has coordinates $latex (-1,~ 3,~ 2)$, and point $latex Q$ has coordinates $latex (3, ~7, ~-1)$, we have:
$$\overrightarrow{OP} = \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}$$
$$\overrightarrow{OQ} = \begin{pmatrix} 3 \\ 7 \\ -1 \end{pmatrix}$$
Now, we are going to find the direction vector ($latex \vec{PQ}$) of the line. This vector is equal to the difference between the position vectors of points P and Q:
$$\overrightarrow{PQ} = \overrightarrow{OQ} ~-~ \overrightarrow{OP}$$
$$\overrightarrow{PQ} = \begin{pmatrix} 3 \\ 7 \\ -1 \end{pmatrix} – \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 4 \\ 4 \\ -3 \end{pmatrix}$$
Now, we can write the vector equation of the line:
$latex \vec{r} = \overrightarrow{OP} + t~\overrightarrow{PQ}$
$$\vec{r} = \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix} + t \begin{pmatrix} 4 \\ 4 \\ -3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -1+4t \\ 3+4t \\ 2-3t \end{pmatrix}$$
EXAMPLE 5
Given a point U(-3, 5, 2) on the line and the direction vector of the line $latex \vec{f} = -1\hat{i}+ 4\hat{j} +3\hat{k }$, find the vector equation of the line.
Solution
We start by finding the position vector of point U with coordinates $latex (-3,~ 5, ~2)$ is:
$$\overrightarrow{OU} = \begin{pmatrix} -3 \\ 5 \\ 2 \end{pmatrix}$$
In this case, the direction vector of the line is:
$$\vec{f} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix}$$
Now, we write the vector equation of the line using this information:
$latex \vec{r} = \overrightarrow{OU}+ t~\vec{f}$
$$\vec{r} = \begin{pmatrix} -3 \\ 5 \\ 2 \end{pmatrix} + t \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -3-t \\ 5+4t \\ 2+3t \end{pmatrix}$$
EXAMPLE 6
Given two points $latex S(6,~ 4,~ -1)$ and $latex T(0,~ -2, ~3)$, what is the vector equation of the line that passes through these points?
Solution
The position vectors ($latex \overrightarrow{OS}$) and ($latex \overrightarrow{OT}$) are:
$$\overrightarrow{OS} = \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix}$$
$$\overrightarrow{OT} = \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix}$$
Now, we are going to find the direction vector ($latex \vec{ST}$) of the line:
$$\overrightarrow{ST} = \overrightarrow{OT} ~-~ \overrightarrow{OS}$$
$$\overrightarrow{ST} = \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix} – \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} -6 \\ -6 \\ 4 \end{pmatrix}$$
Then, the vector equation of the line is:
$latex \vec{r} = \overrightarrow{OS} + t~\overrightarrow{ST}$
$$\vec{r} = \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix} + t \begin{pmatrix} -6 \\ -6 \\ 4 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 6+-6t \\ 4-6t \\ -1+4t \end{pmatrix}$$
EXAMPLE 7
Find the vector equation of the line that passes through the two points A(1, 2, -1) and B(1, 1, 2) and determine whether the point P(1, 3, 1) lies on the line.
Solution
The position vectors of the given points are:
$$\overrightarrow{OA} = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}$$
$$\overrightarrow{OB} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$$
The direction vector ($latex \vec{AB}$) of the line is:
$$\overrightarrow{AB} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} – \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix}$$
Then, the vector equation of the line is:
$latex \vec{r} = \overrightarrow{OA} + t~\overrightarrow{AB}$
$$\vec{r} = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + t \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix}$$
To determine if P lies on the line, we need to find the value of $latex t$. Comparing the components of the vector equation and the position of the point, we have:
$latex 1=1$
$latex 2-t=3~~(t=-1)$
$latex -1+3t=1~~(t=\frac{2}{3})$
The last two equations are not compatible, so the point P is not on the line.
EXAMPLE 8
Find the vector equations of the lines $latex \overrightarrow{AB}~$ and $latex ~\overrightarrow{CD}$, with the points $latex A(1, ~2,~ -1)$, $latex B(1 , ~1,~ 2)$, $latex C(0, ~1, ~2)~$ and $latex ~D(-1,~ 3,~ -4)$.
Find the point of intersection of the lines.
Solution
The vector equation for ($latex \overrightarrow{AB}$) was found in the previous example. Then, we have:
$$\vec{r} = \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix}$$
The line $latex \overrightarrow{CD}$ is given by $latex \vec{r}=\overrightarrow{OC}+s~\overrightarrow{CD}$. Therefore, we have:
$$\vec{r} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + s \begin{pmatrix} -1 \\ 2 \\ -6 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -s\\ 1+2s \\ 2-6s \end{pmatrix}$$
The lines $latex \overrightarrow{AB}~$ and $latex ~\overrightarrow{CD}$ intersect if the parameters $latex s$ and $latex t$ satisfy the following:
$$ \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix} = \begin{pmatrix} -s\\ 1+2s \\ 2-6s \end{pmatrix}$$
From the first row, we have $latex 1=-s$. Then, for the lines to intersect, we must have $latex s=-1$.
From the second row:
$latex 2 − t = 1 + 2s$
$latex 2 − t = −1$
$latex t = 3$
Substituting $latex s=-1$ and $latex t=3$ in the third row $latex −1 + 3t = 2 − 6s$, we get $latex 8 = 8$. Then, the values of $latex s$ and $latex t$ satisfy all three equations.
The point of intersection is found by substituting $latex s=-1$ or $latex t=3$ into $latex \overrightarrow{AB}~$ or $latex ~\overrightarrow{CD}$ respectively.
The point of intersection is $latex (1,~ −1, ~8)$.
Vector equation of the line – Practice problems
See also
Interested in learning more about vectors? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
