Two or more vectors can be added using both graphical and algebraic methods. The three main methods for adding vectors are the polygon method, the parallelogram method and vector addition using its components.
Here, we will look at some examples with answers and practice problems for the topic of vector addition. We will use the three methods mentioned.
10 Vector addition examples with answers
If you need a revision of the methods for vector addition, you can visit this article.
EXAMPLE 1
Find the addition of the following vectors using the polygon method:
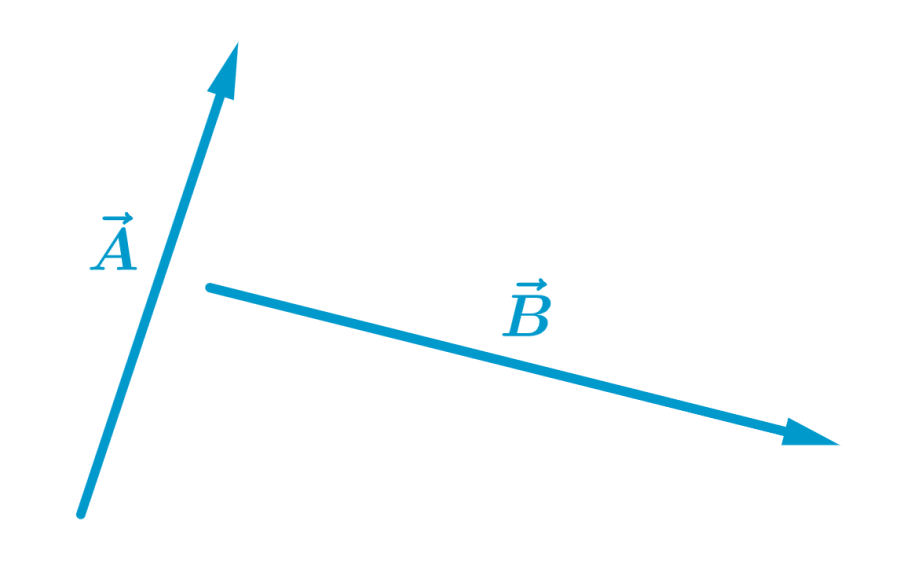
Solution
To find the addition of the vectors by the polygon method, we have to place the base of one of the vectors at the tip or head of the other vector.
Then, we place the base of vector $latex \vec{B}$ at the head of vector $latex \vec{A}$:
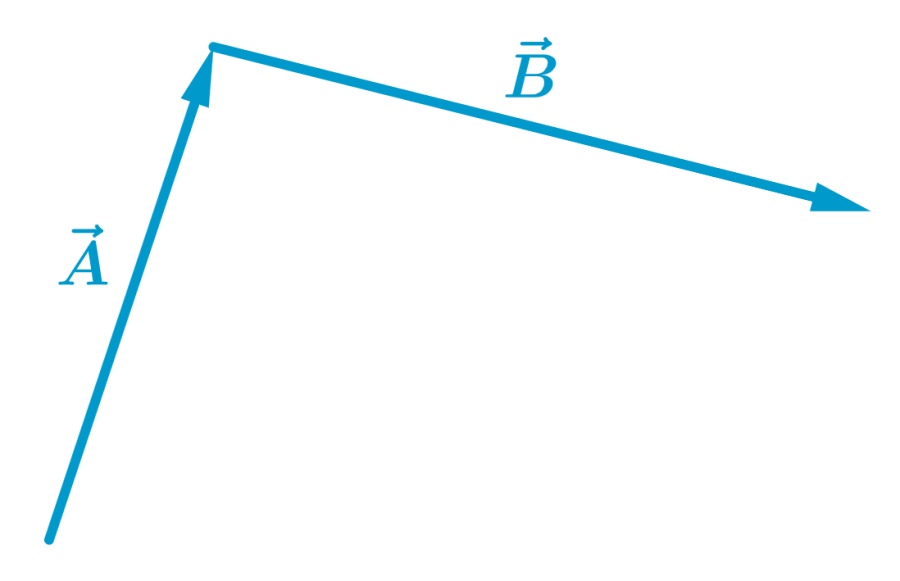
The resulting vector, $latex \vec{R}$, is the vector that joins the base or tail of the first vector to the head of the second vector:
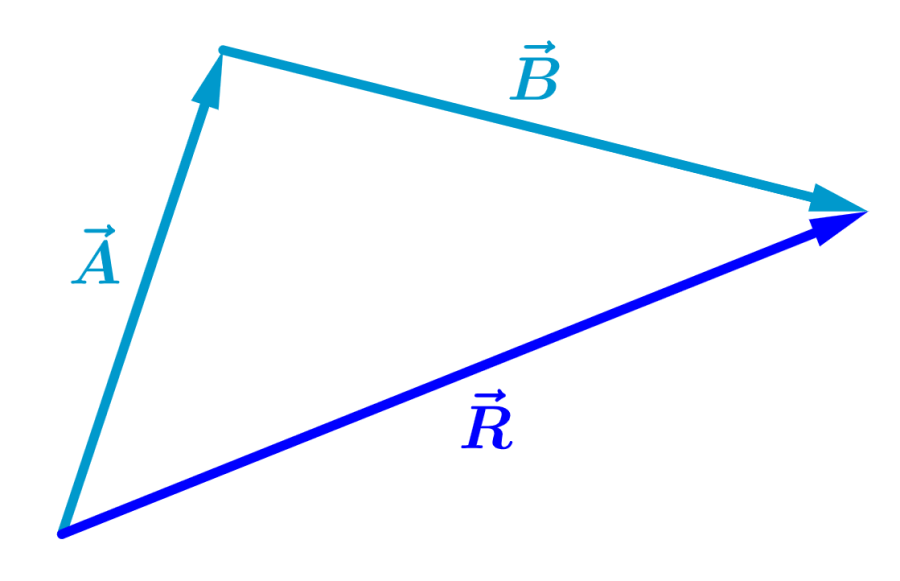
The order in which we add vectors doesn’t matter. That is, we can add the vectors in the opposite order, and get the same result:
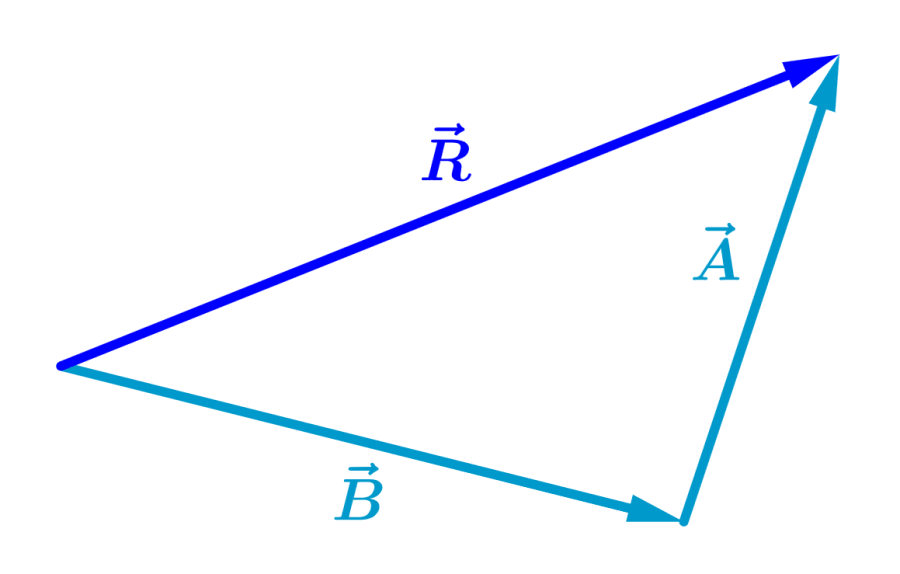
.
EXAMPLE 2
Find the addition of the following three vectors using the polygon method:
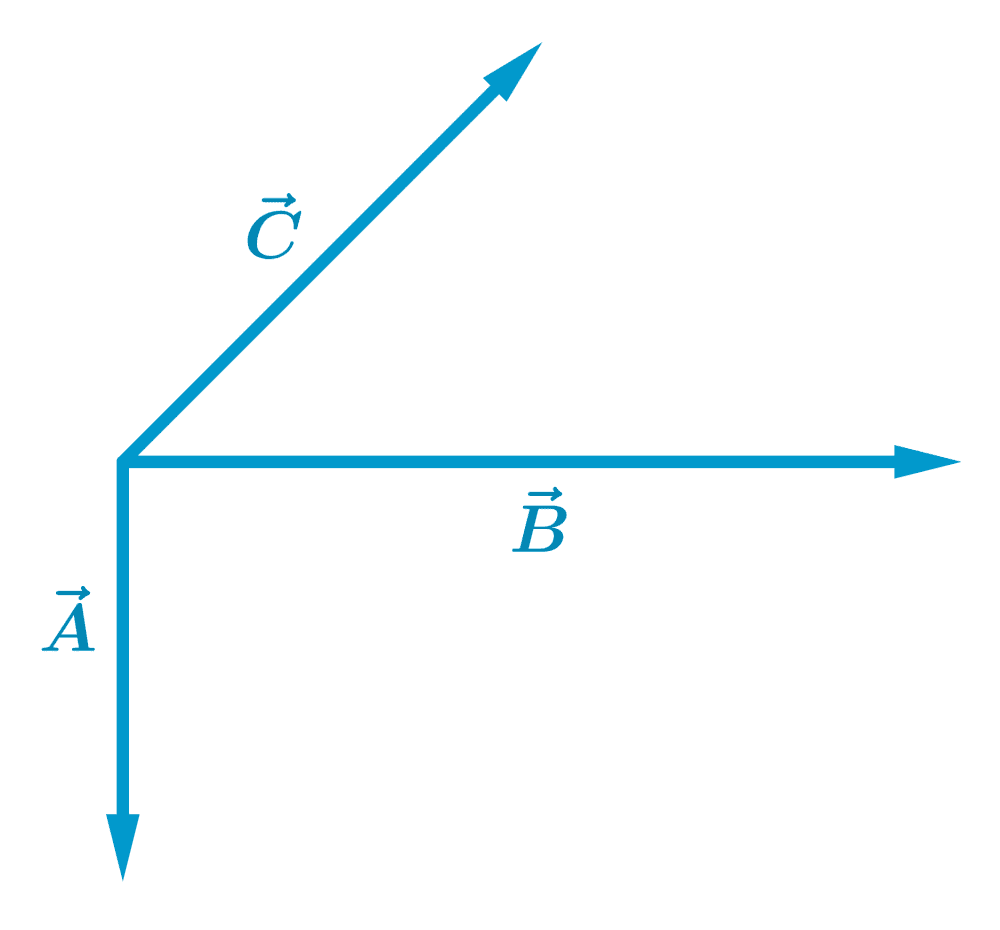
Solution
Let’s start by adding two of the vectors, and then add the resulting vector to the third vector.
Then, we start by adding the vectors $latex \vec{A}$ and $latex \vec{B}$ to obtain the vector $latex \vec{D}$:
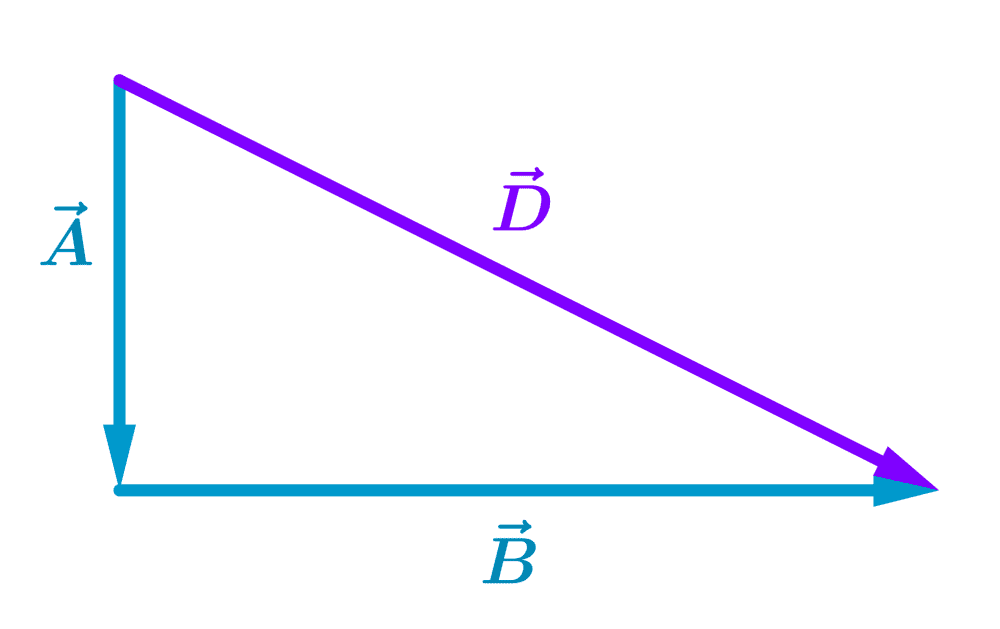
Now, we add the vector $latex \vec{C}$ to the vector $latex \vec{D}$ to obtain the final result $latex \vec{R}$:
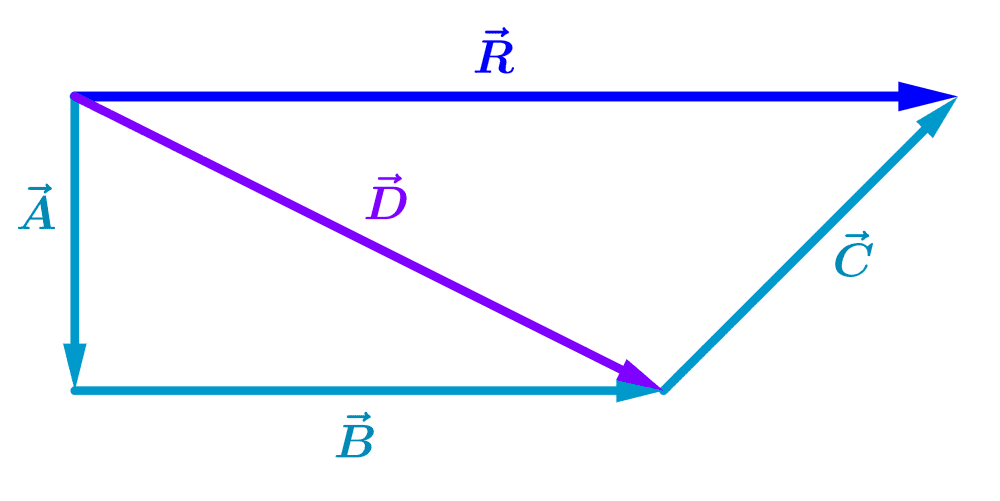
Similar to the previous example, the addition can be performed in any other order.
EXAMPLE 3
Charles goes for a ride on his bicycle. He decides to travel 10 km to the North and then 20 km to the East. Find the distance and direction of his final position.
Solution
We can use a diagram to represent the addition of the vectors showing the travel of 10 km to the North and 20 km to the East:
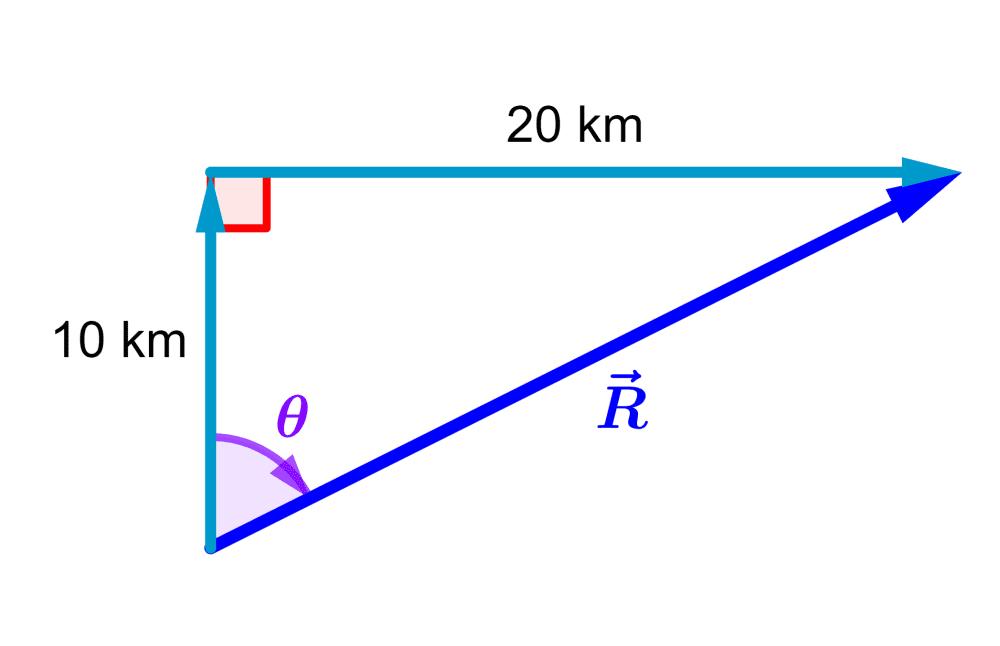
Then, the distance and direction of its final position are found by determining the magnitude (length) and angle of the vector $latex \vec{R}$.
The vectors form a right angle with each other, so the triangle formed is a right triangle and we can use the Pythagorean theorem.
The distance from the starting point to the final point is equal to the hypotenuse of the triangle, and we have:
$$\sqrt{(10\text{ km})^2+(20\text{ km})^2}=22.36\text{ km}$$
To find the angle θ, we use the tangent function:
$$\tan(\theta)=\frac{\text{opuesto}}{\text{adyacente}}=\frac{20\text{ km}}{10\text{ km}}=2$$
$$\theta=\tan^{-1}(2)=63.4^{\circ}$$
Then, Charles is 22.36 km away in a direction of 63.4° from north to east (positive x-axis).
EXAMPLE 4
Use the parallelogram method to add the following vectors:
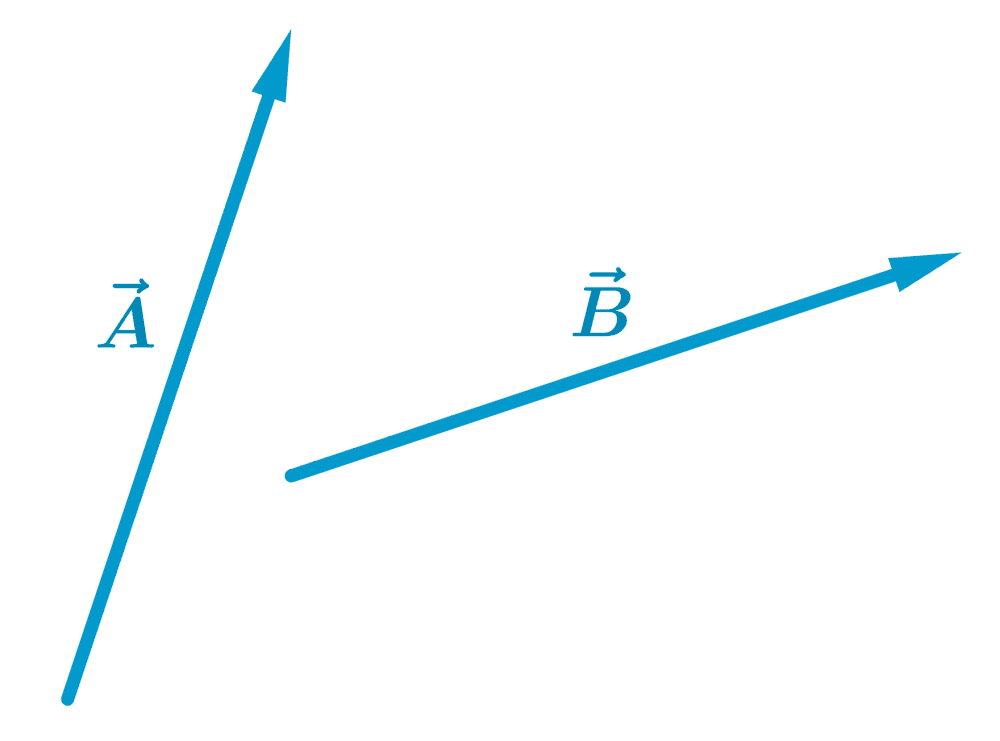
Solution
The parallelogram method consists of placing the vectors with their bases at the same point, as follows:
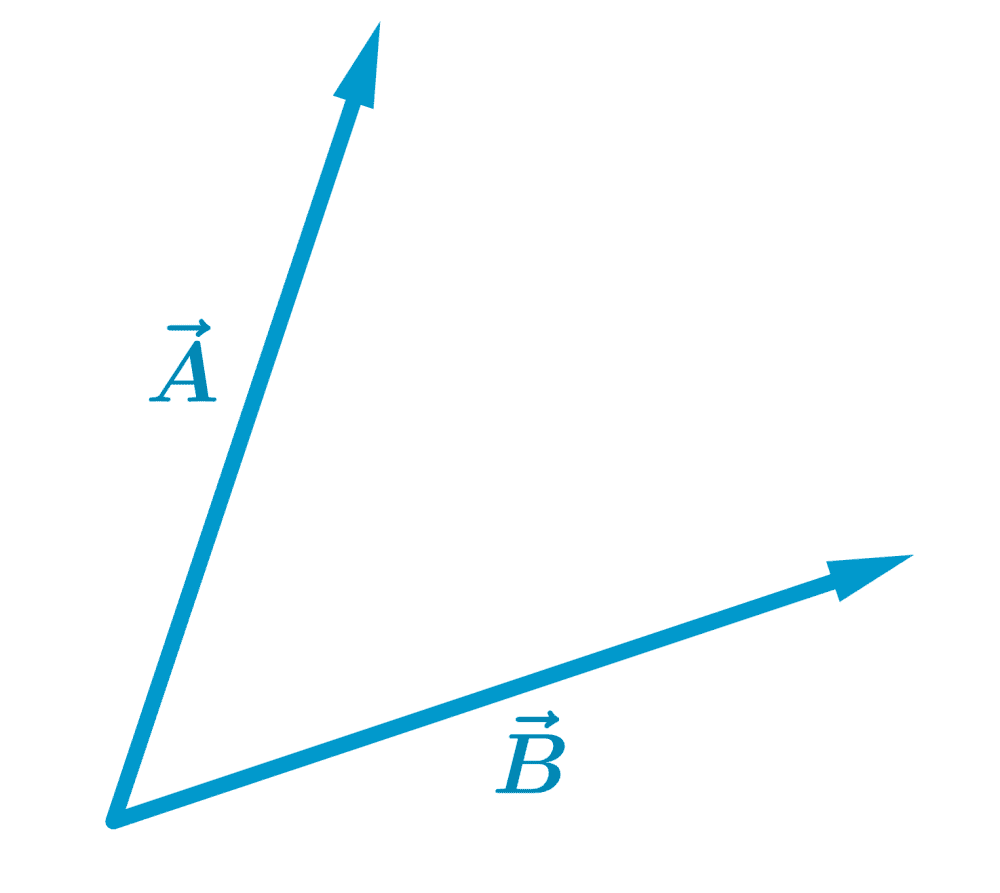
Then, we draw a parallelogram using the initial vectors as adjacent sides:
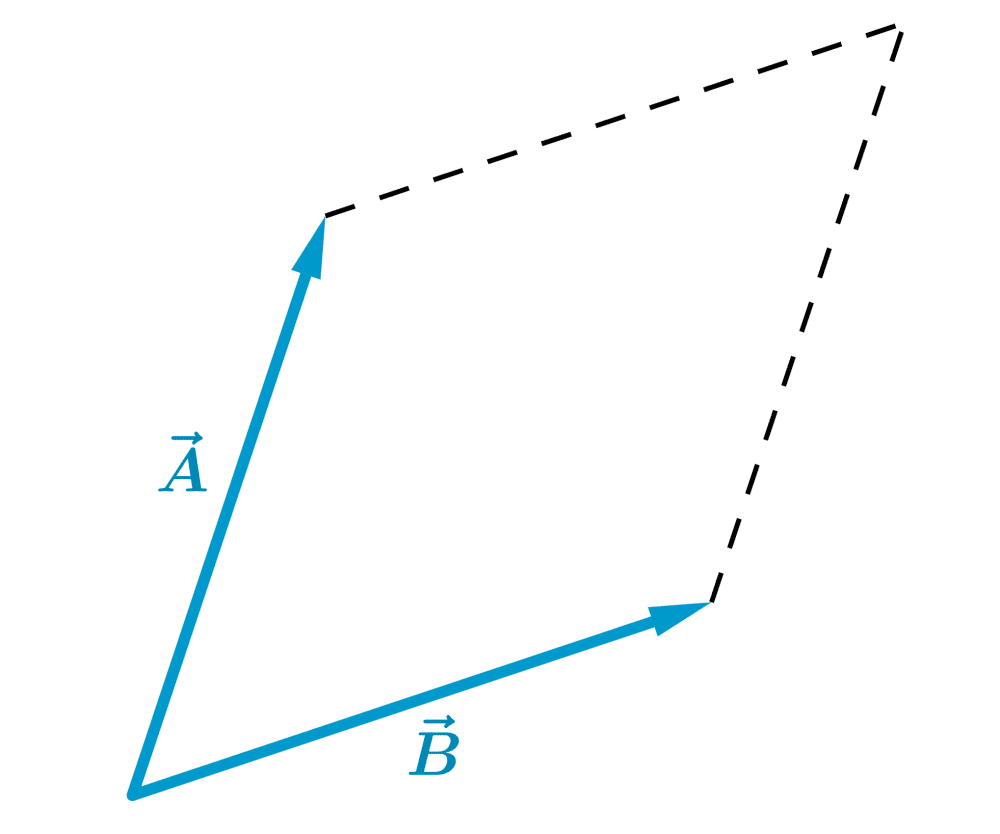
The diagonal of the parallelogram formed represents the addition of the vectors:
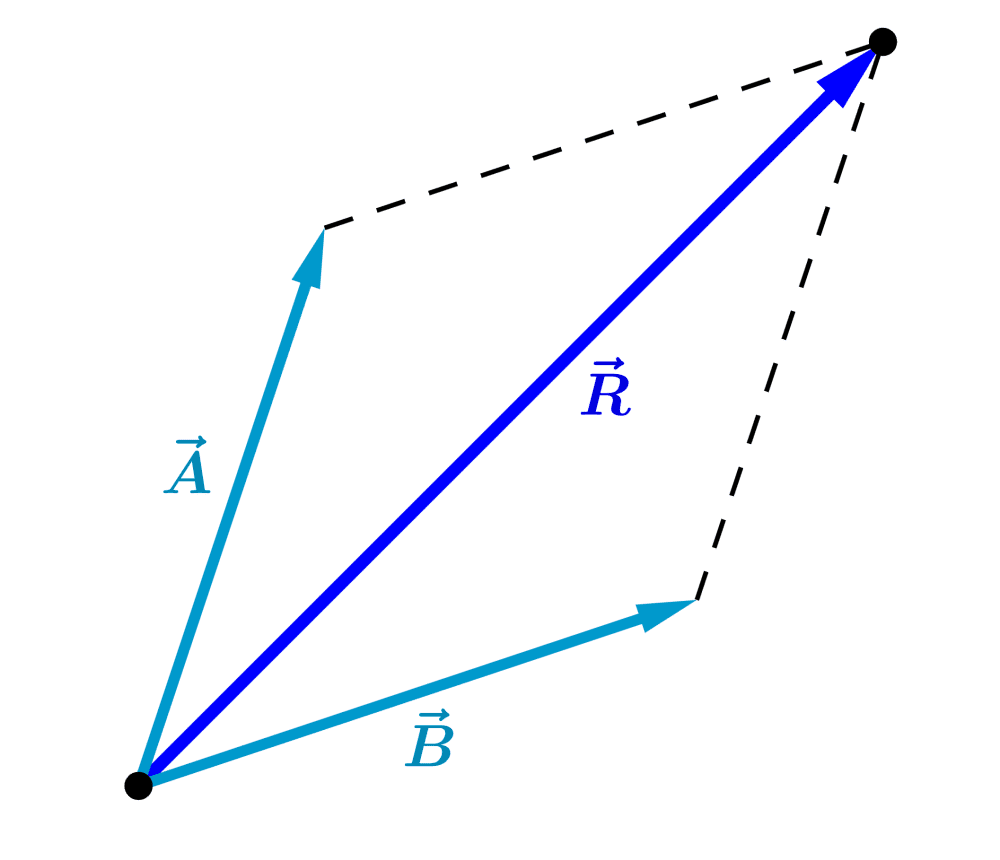
.
EXAMPLE 5
Find the addition of the vectors using the parallelogram method:
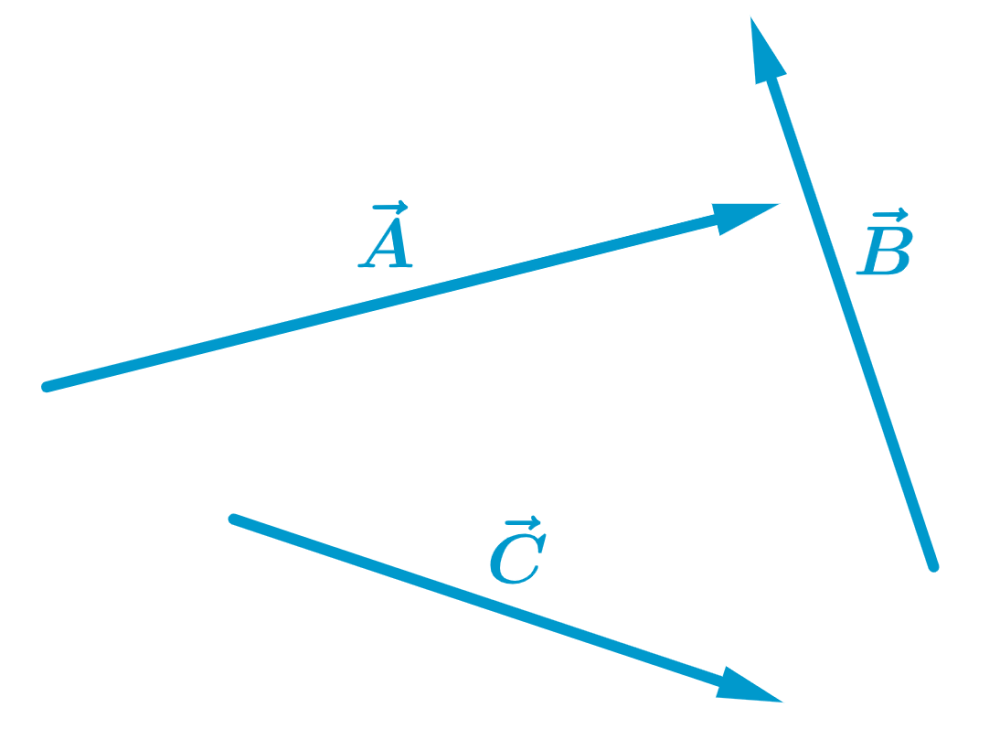
Solution
We start by adding two of the vectors to obtain the following result:
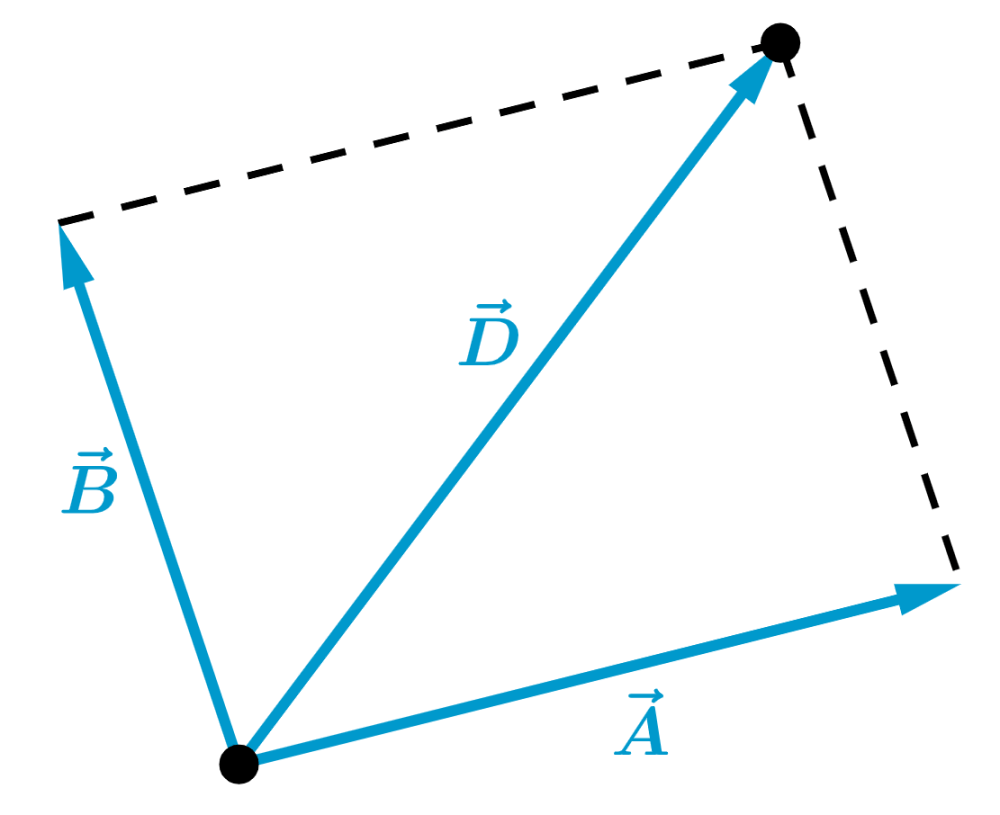
Now, we add the resultant vector with the third vector and we have:
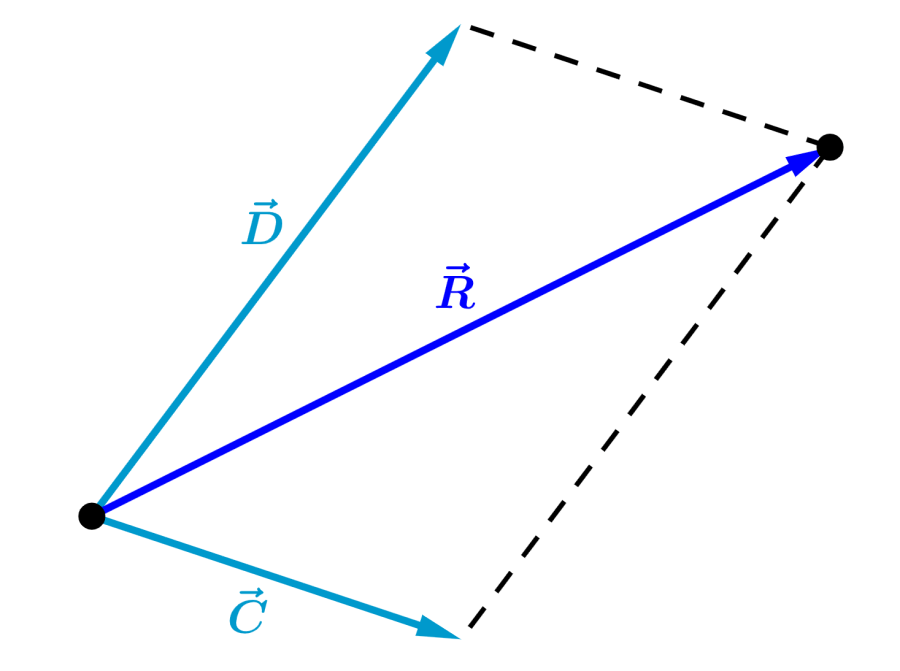
.
EXAMPLE 6
Add the vectors $latex \vec{u}=2i+4j+5k$ and $latex \vec{v}=3i+j+2k$.
Solution
In this case, we have the components of the vectors. In this notation, the letters $latex i,~j,~ k$ represent the components in $latex x,~ y$, and $latex z$ respectively.
To add two or more vectors, we simply add their components to obtain the resulting vector $latex \vec{R}$. Then, we have:
$$R_{x}=u_{x}+v_{x}=2+3=5$$
$$R_{y}=u_{y}+v_{y}=4+1=5$$
$$R_{z}=u_{z}+v_{z}=5+2=7$$
Then, the addition of the vectors is
$latex \vec{R}=5i+5j+7k$
EXAMPLE 7
Add the vectors $latex \vec{u}=-6i+8j+7k$ and $latex \vec{v}=3i-4j+5k$.
Solution
Similar to the previous exercise, we simply have to add the components of the vectors to find their sum. Then, we have:
$$R_{x}=u_{x}+v_{x}=-6+3=-3$$
$$R_{y}=u_{y}+v_{y}=8-4=4$$
$$R_{z}=u_{z}+v_{z}=7+5=12$$
Then, the addition of the vectors is
$latex \vec{R}=-3i+4j+12k$
EXAMPLE 8
Find the addition of the vectors $latex \vec{u}=12i-9j+11k$, $latex \vec{v}=-5i-7j+7k$ and $latex \vec{w}=2i-3j+k$.
Solution
To find the addition of the vectors, let’s add each of their components:
$$R_{x}=u_{x}+v_{x}+w_{x}=12-5+2=9$$
$$R_{y}=u_{y}+v_{y}+w_{y}=-9-7-3=-19$$
$$R_{z}=u_{z}+v_{z}+w_{z}=11+7+1=19$$
Then, the vector that represents the addition of the vectors is
$latex \vec{R}=9i-19j+19k$
EXAMPLE 9
Find the resultant vector by adding the following vectors:
$latex \vec{M}$: 20 m, 60° from the east to the north
$latex \vec{N}$: 10 m, 30° from the east to the north
Solution
To find the addition of the vectors, we have to start by finding the components in $latex x$ and in $latex y$ of the two given vectors.
We can find the $latex x$ component using cosine and the $latex y$ component using sine. Then, we have:
$$M_{x}=M\cos (\theta)=(20\text{ m})(\cos(60^{\circ})=10\text{ m}$$
$$M_{y}=M\sin (\theta)=(20\text{ m})(\sin(60^{\circ})=17.32\text{ m}$$
$$N_{x}=N\cos (\theta)=(10\text{ m})(\cos(30^{\circ})=8.66\text{ m}$$
$$N_{y}=N\sin (\theta)=(10\text{ m})(\sin(30^{\circ})=5\text{ m}$$
Now, we just add up the components:
$$R_{x}=M_{x}+N_{x}=10\text{ m}+8.66\text{ m}=18.66\text{ m}$$
$$R_{y}=M_{y}+N_{y}=17.32\text{ m}+5\text{ m}=22.32\text{ m}$$
Then, the addition of the vectors is $latex \vec{R}=18.66i+22.32j$.
EXAMPLE 10
What is the addition of the following vectors?
$latex \vec{A}$: 30 m, 45° from the east to the north
$latex \vec{B}$: 40 m, 30° from the east to the north
Solution
We have to start by finding the components in $latex x$ and in $latex y$. Then, we have:
$$A_{x}=A\cos (\theta)=(30\text{ m})(\cos(45^{\circ})=21.21\text{ m}$$
$$A_{y}=A\sin (\theta)=(30\text{ m})(\sin(45^{\circ})=21.21\text{ m}$$
$$B_{x}=B\cos (\theta)=(40\text{ m})(\cos(30^{\circ})=34.64\text{ m}$$
$$B_{y}=B\sin (\theta)=(40\text{ m})(\sin(30^{\circ})=20\text{ m}$$
Then, the components of the vector formed by the addition are:
$$R_{x}=A_{x}+B_{x}=21.21\text{ m}+34.64\text{ m}=55.85\text{ m}$$
$$R_{y}=A_{y}+B_{y}=21.21\text{ m}+20\text{ m}=41.21\text{ m}$$
The resulting vector is $latex \vec{R}=55.85i+41.21j$.
Vector addition – Practice problems


See also
Interested in learning more about vectors? You can take a look at these pages:



