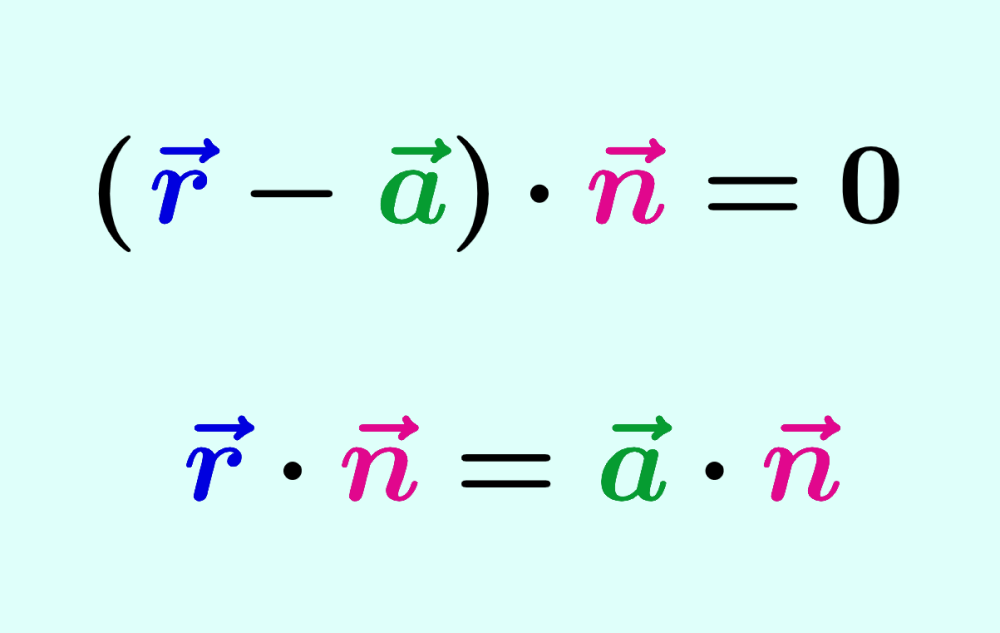The vector equation of a plane allows us to describe the position of each point on a plane. There are two main methods to describe a plane, with a point on the plane and a vector perpendicular to the plane, or with three points on the plane.
In this article, we will learn how to find the vector equation of the plane using the two methods mentioned above. Then, we will look at some examples where we will apply these cases.
How to find the vector equation of a plane?
To find the vector equation of a plane, we can use two main methods, depending on the information we have:
- A point on the plane and a vector perpendicular to the plane
- Three points on the plane that do not lie on a straight line
First case
We start with a point $latex A $ and a vector $latex \vec{n}$, which is normal (perpendicular) to the plane:
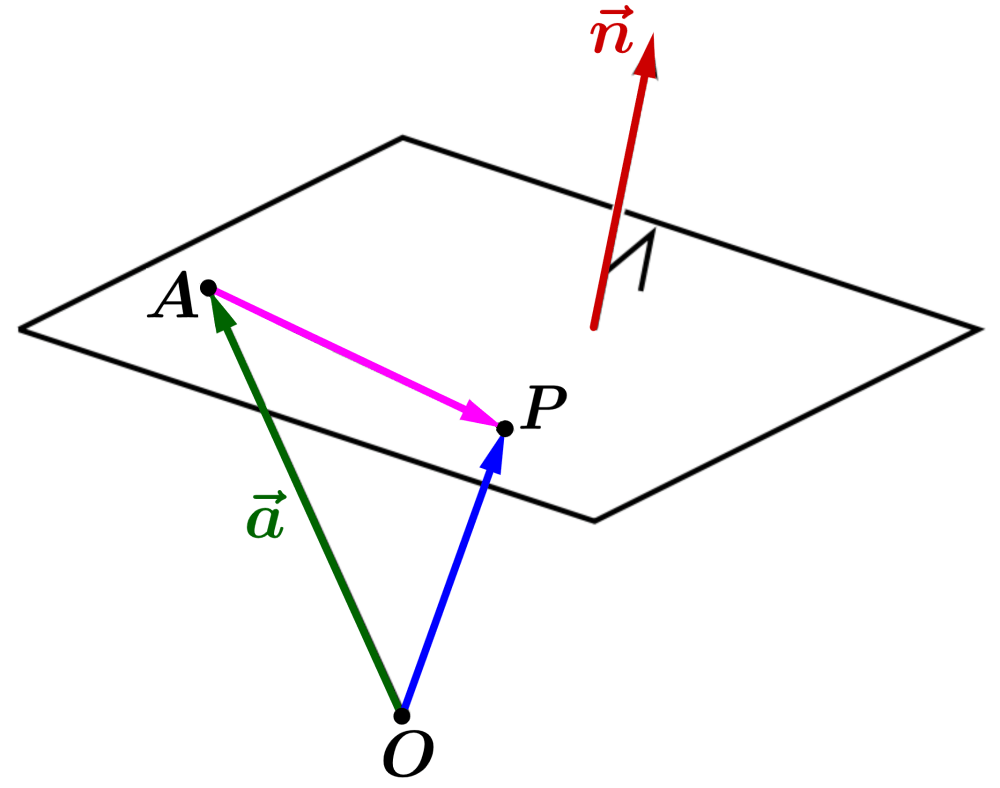
Every vector parallel to the plane is perpendicular to $latex \vec{n}$. This means that if any point $latex P $ is in the plane, we must have:
$latex \overrightarrow{AP}\cdot \vec{n}=0$
(the dot product of two perpendicular vectors is 0)
In the diagram, we see that $latex \vec{r}$ is the addition of $latex \vec{a}$ and $latex \overrightarrow{AP}$. Then, we have $latex \overrightarrow{AP}=\vec{r}-\vec{a}$, so the equation of the plane is:
$latex \overrightarrow{AP}\cdot \vec{n}=0$
$latex (\vec{r}-\vec{a})\cdot \vec{n}=0$
This can also be written as $latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$.
To convert to cartesian coordinates, we can use $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$.
Second case
In this case, suppose we have three points that lie on the plane and are not part of the same straight line.
We can use the cross product to create a vector orthogonal (perpendicular) to the plane and proceed with the same process used in the first case.
For example, if we know that points A, B, and C lie on the plane, we can write:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
Then, we use the equation $latex (\vec{r}-\vec{a})\cdot \vec{n}=0$.
Solved examples on vector equation of a plane
EXAMPLE 1
Find the equation of the plane that passes through the point $latex A(1, ~0,~2)$ and in which, $latex \vec{n}=\hat{i}-\hat{j}+\ hat{k}$ is a vector perpendicular to the plane.
Solution
Here, we have a point on the plane and a perpendicular vector. Then, we can use the following equation:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
In this case, we have $latex \vec{a}=\hat{i}+2\hat{k}$, so
$latex \vec{a}\cdot \vec{n}=1+0+2=3$
Also, given that $latex \vec{n}=\hat{i}-\hat{j}+\hat{k}$, we have:
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}=3$
To convert to Cartesian coordinates, we consider $latex (x,~y,~z)$ to be the coordinates of any point $latex P$ on the plane.
Entonces, tenemos $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ y $latex \vec{r}\cdot \vec{n}=x-y+z$:
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}=3$
$latex x-y+z=3$
EXAMPLE 2
The point $latex A(3, ~2,~1)$ lies in a plane and the vector $latex \vec{n}=2\hat{i}-2\hat{j}+\hat{k} $ is a vector perpendicular to the plane. Find the equation of the plane.
Solution
Similar to the previous example, we will use the following formula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Since we have the position vector $latex \vec{a}=3\hat{i}+2\hat{j}+\hat{k}$, we can write:
$latex \vec{a}\cdot \vec{n}=6-4+1=3$
Since the vector perpendicular to the plane is $latex \vec{n}=2\hat{i}-2\hat{j}+\hat{k}$, we have:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix}=3$
Using $latex (x,~y,~z)$ as the coordinates of a point $latex P$ on the plane, we have $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix}=3$
$latex 2x-2y+z=3$
EXAMPLE 3
Given a point $latex A(5,~ -2,~ 3)$ on a plane and the perpendicular vector $latex \vec{n} = 2\hat{i} -3\hat{j} +1\hat{ k}$, find the equation of the plane.
Solution
Let’s use the following formula to find the equation of the plane:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Since we have the position vector $latex \vec{a}=5\hat{i}-2\hat{j}+3\hat{k}$, we can write:
$latex \vec{a}\cdot \vec{n}=10+6+3=19$
Using the perpendicular vector $latex \vec{n}=2\hat{i}-3\hat{j}+\hat{k}$, we have:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}=19$
Using $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ to write in Cartesian coordinates:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}=19$
$latex 2x-3y+z=19$
EXAMPLE 4
Find the vector equation of the plane that passes through the point A(-1, 3, 2) and in which the vector $latex \vec{n} = 2\hat{i} -2\hat{j} -3 \hat{k}$ is perpendicular.
Solution
Similar to the previous examples, we use the following formula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
The position vector of the given point is $latex \vec{a}=-\hat{i}+3\hat{j}+2\hat{k}$. Then, we have:
$latex \vec{a}\cdot \vec{n}=-2-6-6=-14$
Using the perpendicular vector $latex \vec{n}=2\hat{i}-2\hat{j}-3\hat{k}$, we have:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix}=-14$
Using $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ to write in Cartesian coordinates:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix}=-14$
$latex 2x-2y-3z=-14$
EXAMPLE 5
Find the equation of the plane that passes through the points A(1, 1, 1), B(2, 1, 0), and C(1, 2, −1).
Solution
In the previous examples, we saw how to find the equation of the plane when we have a point and a perpendicular vector $latex \vec{n}$.
Then, we have to find a vector $latex \vec{n}$. For this, we can consider that the perpendicular vector is equal to the vector product of two vectors:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(\hat{i}-\hat{k})\times (\hat{j}-2\hat{k})$
$latex \vec{n}=\hat{i}+2\hat{j}+\hat{k}$
Now, we use the following formula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
The position vector of A is $latex \vec{a}=\hat{i}+\hat{j}+\hat{k}$. Then, we have:
$latex \vec{a}\cdot \vec{n}=1+2+1=4$
And the equation of the plane is
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}=4$
In Cartesian form, we have:
$latex x+2y+z=4$
EXAMPLE 6
Given the points $latex A(1,~ 2,~ 3)$, $latex B(2, ~1, ~0)$, and $latex C(0,~ 3,~ 1)$, what is the vector equation of the plane passing through these points?
Solution
To find the perpendicular vector $latex \vec{n}$, we use the following:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(\hat{i}-\hat{j}-3\hat{k})\times (-\hat{i}+\hat{j}-2\hat{k})$
$latex \vec{n}=5\hat{i}+5\hat{j}$
Now, we use the formula for the vector equation of a plane:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
We can use any of the points. The position vector of A is $latex \vec{a}=\hat{i}+2\hat{j}+3\hat{k}$. Therefore, we have:
$latex \vec{a}\cdot \vec{n}=5+10+0=15$
And the equation of the plane is
$latex \vec{r}\cdot \begin{pmatrix} 5 \\ 5 \\ 0 \end{pmatrix}=15$
In Cartesian form, we have:
$latex 5x+5y=15$
EXAMPLE 7
If a plane passes through the points $latex A(2,~ 0, ~1)$, $latex B(0,~ 3,~ -1)$, and $latex C(1,~ -1,~ 3)$, what is its vector equation?
Solution
We start by finding the perpendicular vector $latex \vec{n}$ using the vector product:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(-2\hat{i}+3\hat{j}-2\hat{k})\times (-\hat{i}-\hat{j}+2\hat{k})$
$latex \vec{n}=4\hat{i}+6\hat{j}+5\hat{k})$
Now, we can apply the formula for the vector equation of a plane:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
The position vector of A is $latex \vec{a}=2\hat{i}+\hat{k}$. Then, we have:
$latex \vec{a}\cdot \vec{n}=8+0+5=13$
And the equation of the plane is
$latex \vec{r}\cdot \begin{pmatrix} 4 \\ 6 \\ 5 \end{pmatrix}=13$
In Cartesian form, we have:
$latex 4x+6y+5z=13$
EXAMPLE 8
Find the vector equation of the plane passing through the points $latex A(1, ~1, ~1)$, $latex ~B(-1, ~2, ~0)$, and $latex C(2,~ 3,~ -1)$.
Solution
The perpendicular vector, $latex \vec{n}$, to the plane is:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(-2\hat{i}+\hat{j}-\hat{k})\times (\hat{i}+2\hat{j}-2\hat{k})$
$latex \vec{n}=-5\hat{j}-5\hat{k})$
Now, we use the following formula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Using the position vector of A, $latex \vec{a}=\hat{i}+\hat{j}+\hat{k}$, we have:
$latex \vec{a}\cdot \vec{n}=0-5-5=-10$
And the equation of the plane is
$latex \vec{r}\cdot \begin{pmatrix} 0 \\ -5 \\ -5 \end{pmatrix}=-10$
In Cartesian form, we have:
$latex -5y-5z=-10$
Vector equation of a plane – Practice problems
See also
Interested in learning more about vectors? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
