Vector operations, in addition to allowing a connection between geometry and algebra, serve as a backbone for various disciplines such as computer graphics, engineering, and data science.
In this article, we will learn the basics of vector operations. We will explore addition, scalar multiplication, and dot and cross products, which together provide a complete set of very useful mathematical tools.
Vector addition and subtraction
Two or more vectors can be added or subtracted using graphical methods or algebraic methods. Graphically, we can add vectors using the head-to-tail method and the parallelogram method.
Algebraically, we can add or subtract vectors using their components.
Addition and subtraction of vectors with the head-to-tail method
To add two vectors $latex \vec{A}$ and $latex \vec{B}$ with the head-to-tail method, we place the tail or base of one of the vectors at the head or tip of the other vector:
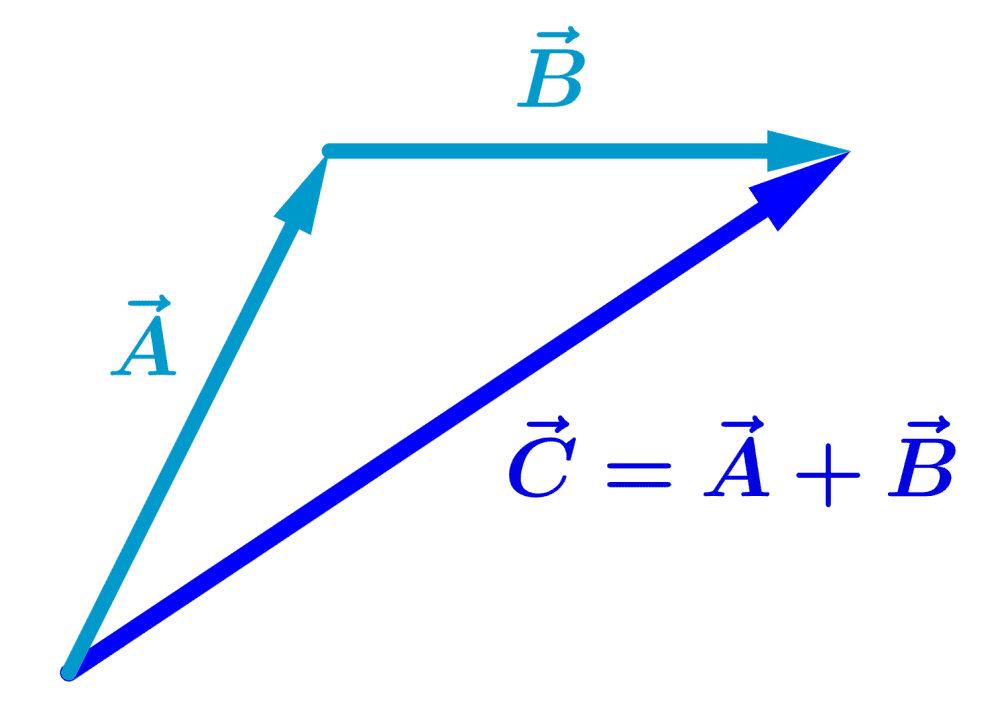
The vector $latex \vec{C}$ is the sum of the vectors $latex \vec{A}$ and $latex \vec{B}$ and is symbolically expressed as:
$latex \vec{C}=\vec{A}+\vec{B}$
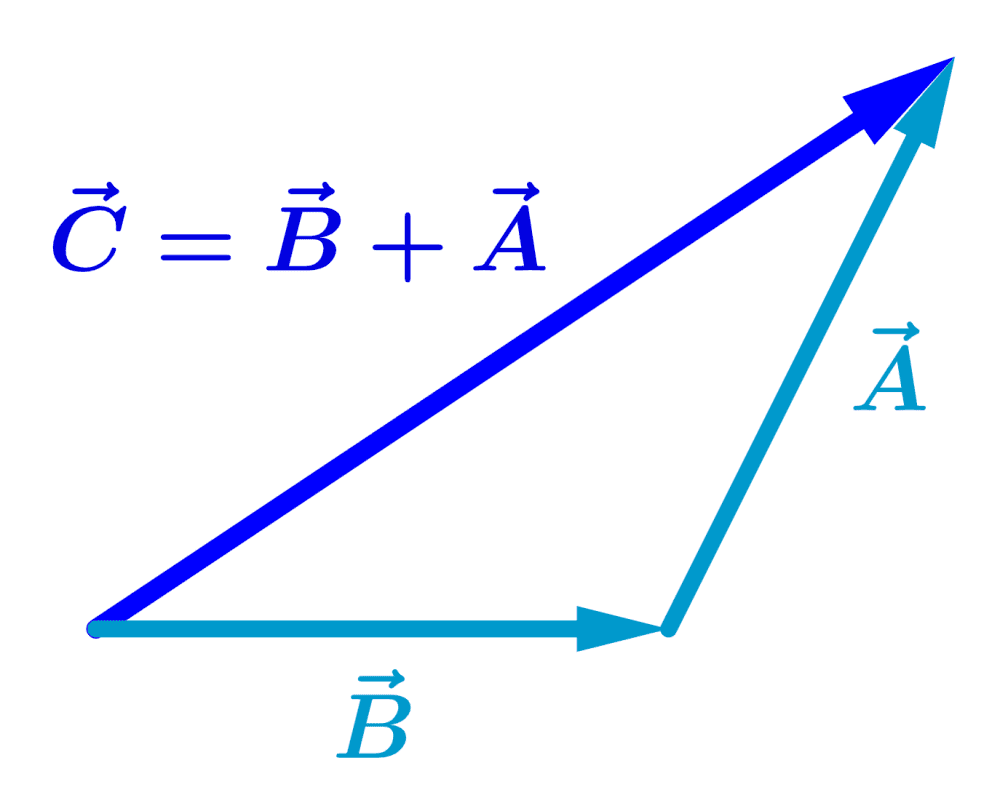
If we add to the vectors in reverse order, that is, $latex \vec{B}$ first and $latex \vec{A}$ second, the result is the same:
To subtract a vector from another vector, we have to change the direction of the vector you are subtracting. For example, to solve $latex \vec{A}-\vec{B}$, we change the direction of the vector $latex \vec{B}$.
In the example above, this would mean changing the direction of the vector as follows:
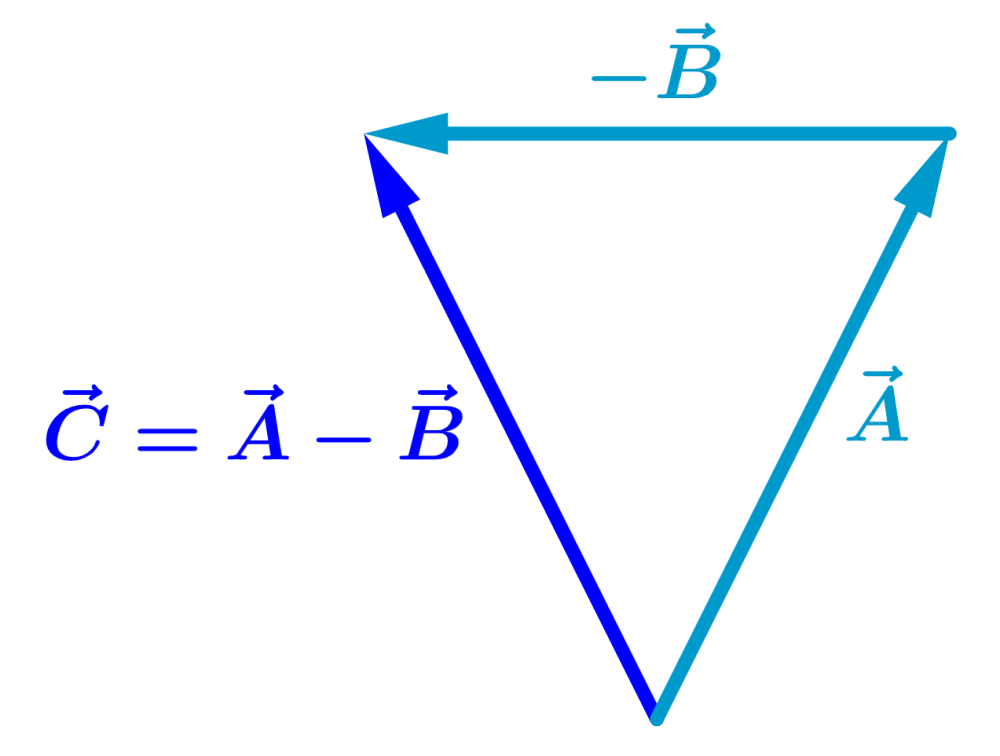
Adding and subtracting vectors with the parallelogram method
To add vectors with this method, we place the vectors with their tails or bases at the same point. Then, we draw a parallelogram in which the vectors are two adjacent sides.
For example, the following diagram represents the addition of the vectors $latex \vec{A}$ and $latex \vec{B}$:
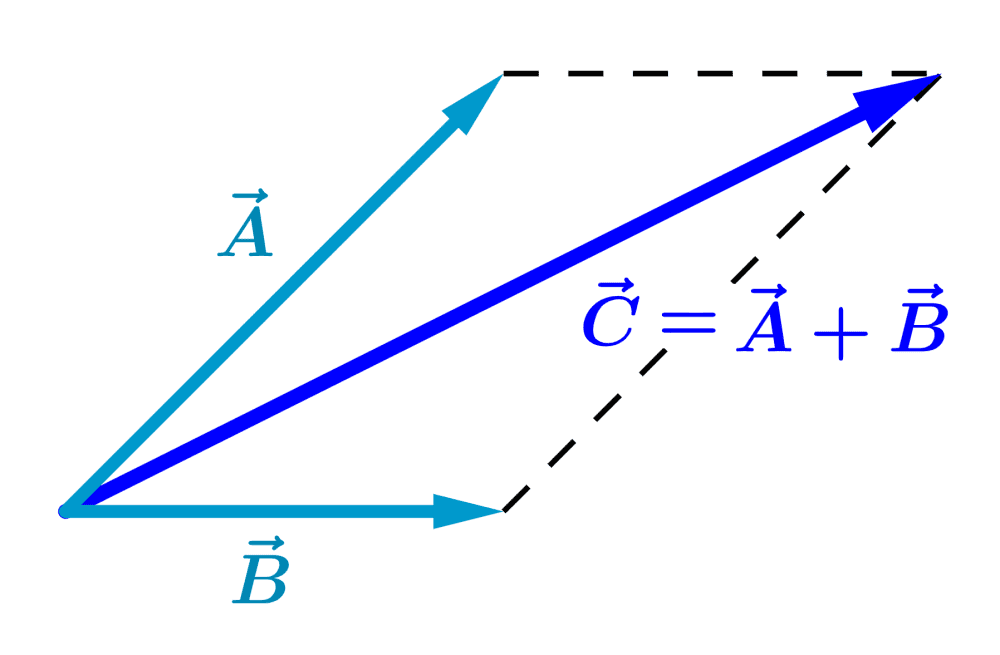
We see that the result of the addition, the vector $latex \vec{C}$, is the diagonal of the parallelogram.
Similar to the previous method, to subtract the vectors, we change the direction of the vector we are subtracting.
Add or subtract vectors using their components
When we know the components of the vectors to be added or subtracted, we can simply add or subtract their components separately.
Suppose we have the following vectors $latex \vec{A}$ and $latex \vec{B}$:
$latex \vec{A}=A_{x}+A_{y}+A_{z}$
$latex \vec{B}=B_{x}+B_{y}+B_{z}$
To find the sum $latex \vec{C}=\vec{A}+\vec{B}$, we just add its components:
$latex C_{x}=A_{x}+B_{x}$
$latex C_{y}=A_{y}+B_{y}$
$latex C_{z}=A_{z}+B_{z}$
Similarly, we simply subtract their components when we have a vector subtraction.
EXAMPLE 1
Use the polygon method to add the following vectors:
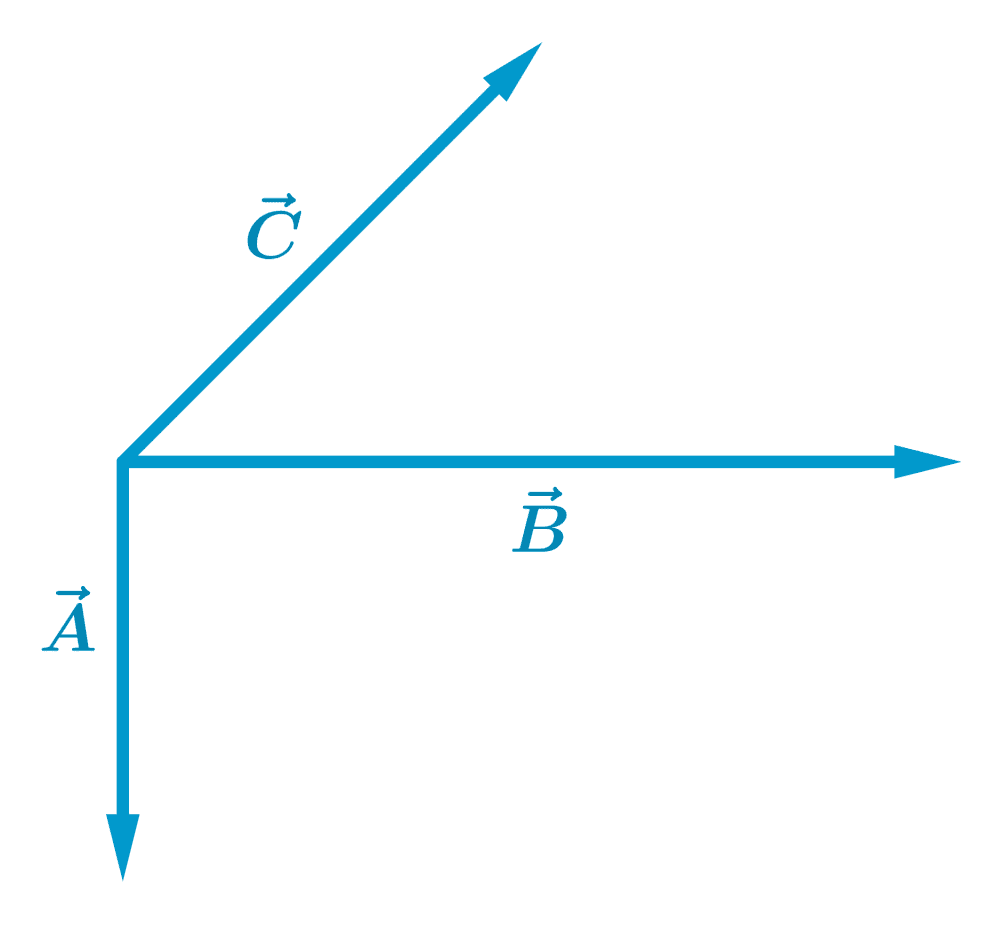
Solution
We can start by adding the vectors $latex \vec{A}$ and $latex \vec{B}$ to obtain the vector $latex \vec{D}$:
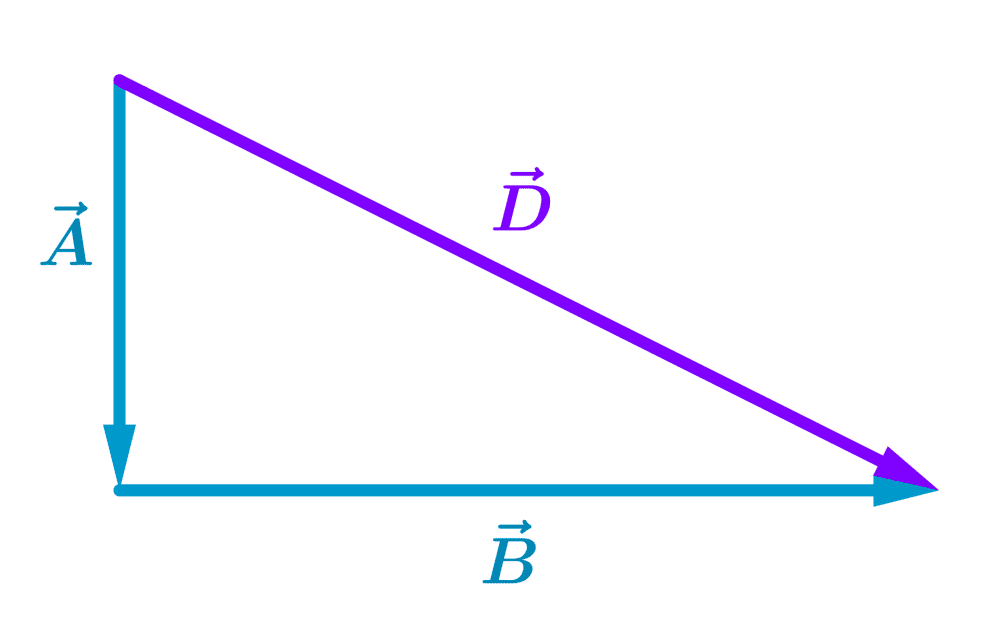
Now, let’s add the vector $latex \vec{C}$ to the vector $latex \vec{D}$ to obtain the final result $latex \vec{R}$:
.
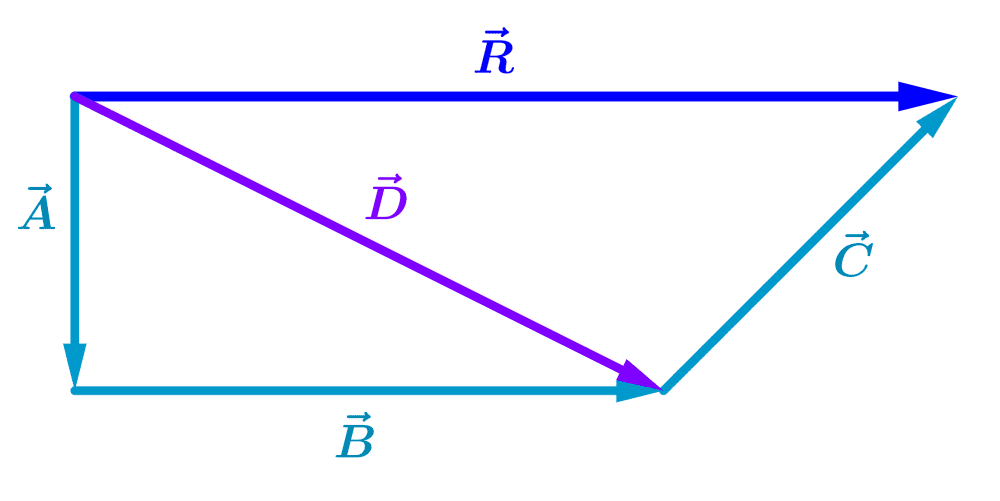
EXAMPLE 2
Add the following vectors using the parallelogram method:
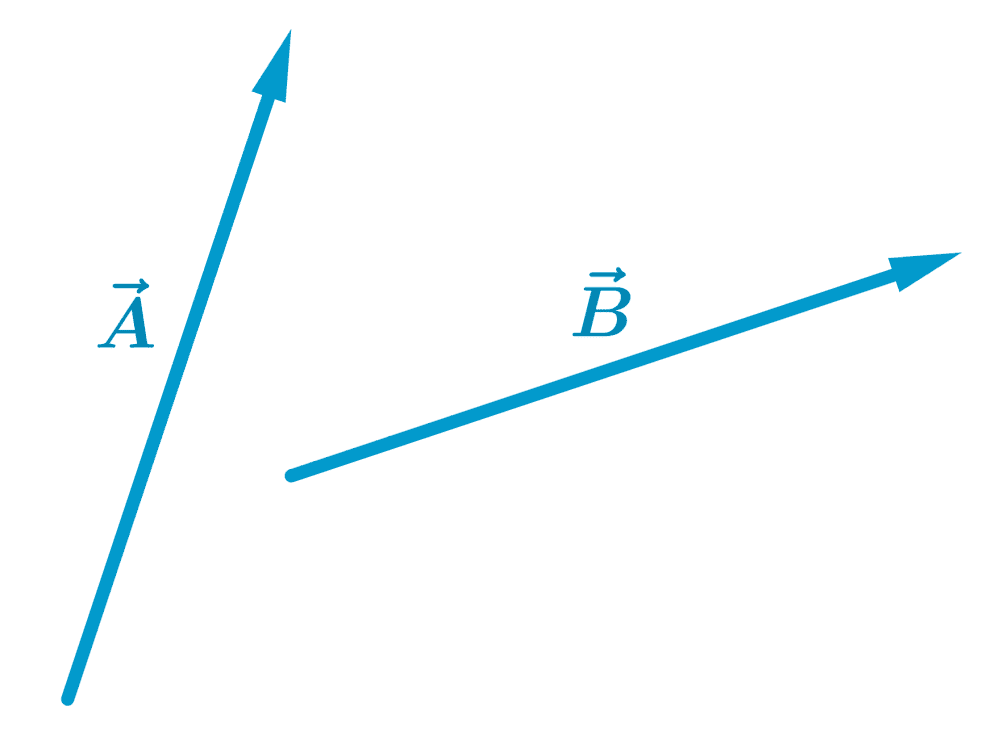
Solution
We place the bases of the vectors at the same point and form a parallelogram, where the vectors are adjacent sides:
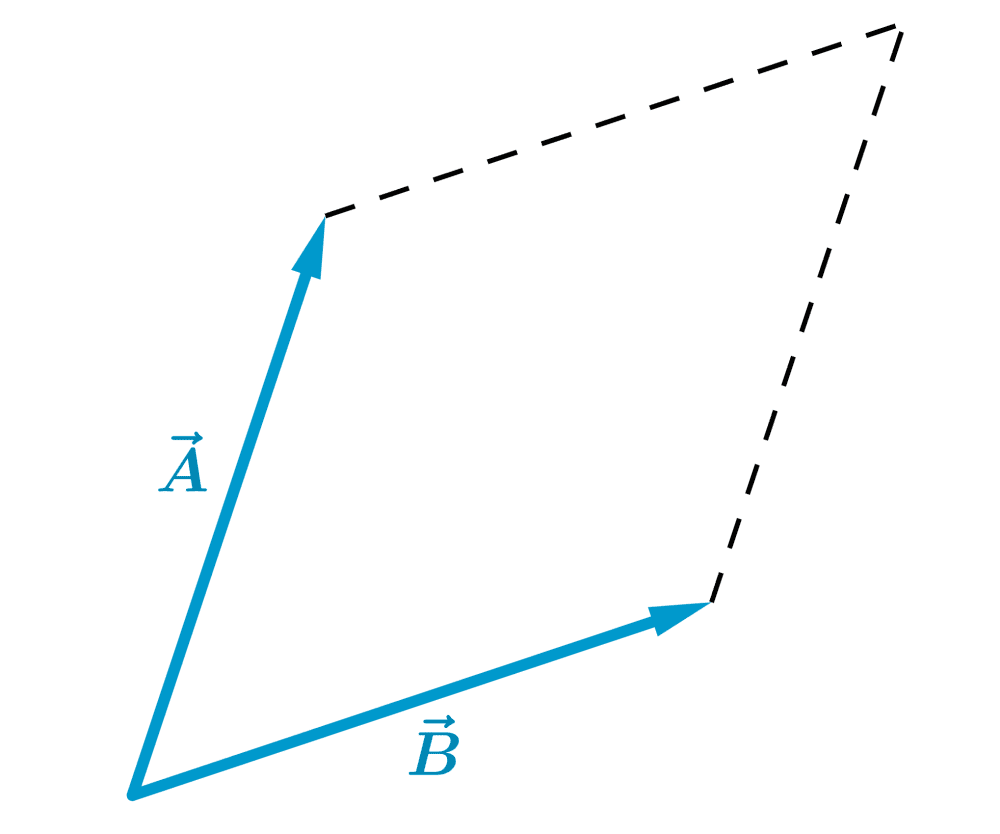
The sum of the vectors is equal to the diagonal of the parallelogram formed:
.
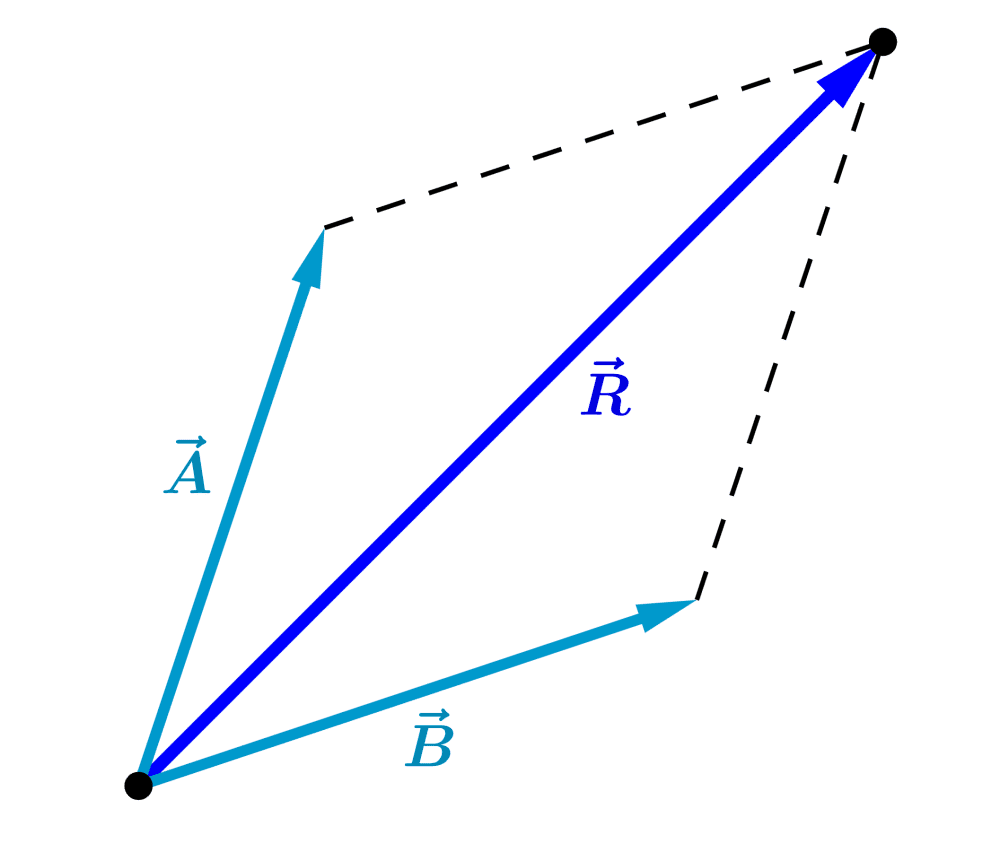
EXAMPLE 3
Add the vectors $latex \vec{A}=3i+2j+5k$ and $latex \vec{B}=2i+j+3k$.
Solution
In this notation, the unit vectors $latex i, ~j,~ k$ represent the coordinates $latex x,~ y,~ z$ respectively.
Then, we simply add the corresponding components of $latex \vec{A}$ and $latex \vec{B}$ to find the addition of the vectors:
$$R_{x}=A_{x}+B_{x}=3+2=5$$
$$R_{y}=A_{y}+B_{y}=2+1=3$$
$$R_{z}=A_{z}+B_{z}=5+3=8$$
Then, the sum of the vectors is
$latex \vec{R}=5i+3j+8k$
Multiplication of vectors by a scalar
The multiplication of vectors by a scalar is easily solved by multiplying the magnitude of the vector or its components by the scalar.
Multiplying vectors by a positive scalar affects the magnitude of the vector, but not its direction:
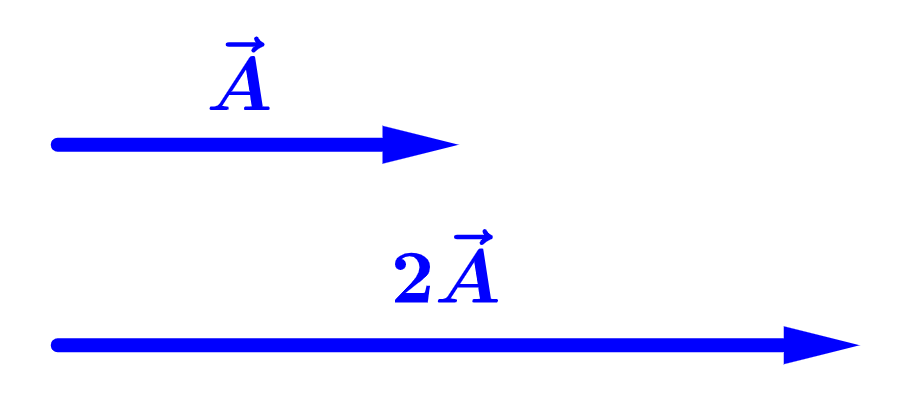
However, when we multiply by a negative scalar, its direction is reversed:
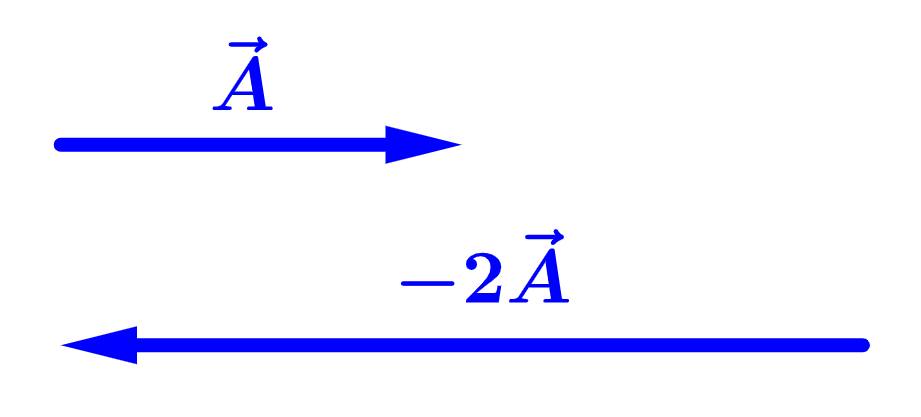
For a vector $latex \vec{A}$ with components $latex A_{x}$ and $latex A_{y}$, multiplication by a scalar $latex k$ is equal to:
$latex R_{x}=kA_{x}$
$latex R_{y}=kA_{y}$
EXAMPLE
Multiply the vector $latex \vec{D} = 2i -5j+ 4k$ by the scalar $latex k = 3$.
Solution
To solve this multiplication, we multiply each component of the vector $latex \vec{D}$ by the scalar $latex k$:
$latex 2i \times 3 = 6i$
$latex -5j \times 3 = -15j$
$latex 4k \times 3 = 12k$
The resulting vector is: $latex \vec{R}= 6i -15j+ 12k$.
Scalar or dot product of vectors
The scalar product of two vectors $latex \vec{A}$ and $latex \vec{B}$ is denoted by $latex \vec{A} \cdot \vec{B}$. The result of the dot product is a scalar quantity.
We can calculate the scalar product using the magnitudes or components of the vectors.
Dot product using magnitudes and angle between vectors
When we know the magnitudes of the vectors and the angle between their directions, we can apply the following formula:
$$\vec{A}\cdot \vec{B}=AB\cos(\theta)$$
where, $latex A$ and $latex B$ are the magnitudes of $latex \vec{A}$ and $latex \vec{B}$ respectively, and $latex \theta$ is the angle between the vectors.
Dot product of vectors using their components
When we know the $latex x,~y,~z$ components of the vectors, we can apply the following formula:
$$\vec{A}\cdot \vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}$$
You can look at the proofs of these formulas in this article: Formulas and properties of dot product of vectors.
EXAMPLE 1
Find the scalar product of vectors A and B, which have magnitudes of 4 and 6, respectively, and the angle between them is 120°.
Solution
We have the following information:
- $latex |A|=4$
- $latex |B|=6$
- $latex \theta=120^{\circ}$
Using the formula given above, we have:
$latex \vec{A} \cdot \vec{B} = |A| ~|B| \cos(\theta)$
$latex = 4 \times 6 \cos(120^{\circ}) $
$$= 24 \left(-\frac{1}{2}\right) $$
$$= -12$$
EXAMPLE 2
We have the vectors $latex \vec{A} = \langle -3,~ 7,~ 1\rangle$ and $latex \vec{B} = \langle 5, ~2,~ 4\rangle$. What is the dot product?
Solution
En este caso, tenemos los componentes de los vectores, por lo que usamos la siguiente fórmula:
$latex \vec{A} \cdot \vec{B} = A_{x} \times B_{x} + A_{y} \times B_{y} + A_z \times B_{z}$
$latex \vec{A} \cdot \vec{B} = (-3 \times 5) + (7 \times 2) + (1 \times 4)$
$latex = -15 + 14 + 4 $
$latex = 3$
Vector product or cross product of vectors
The vector product of two vectors $latex \vec{A}$ and $latex \vec{B}$ is denoted by $latex \vec{A} \times \vec{B}$. The result of the vector product is a vector.
The vector product can be calculated using the magnitudes and the angle between the vectors or using the components of the vectors.
Cross product using magnitudes and angle between vectors
If we know the magnitudes of the vectors and the angle between them, we calculate the magnitude of their vector product with the following formula:
$$\vec{A}\times \vec{B}=AB\sin(\theta)$$
where, $latex A$ and $latex B$ are the magnitudes of $latex \vec{A}$ and $latex \vec{B}$ respectively, and $latex \theta$ is the angle between the vectors.
Vector product direction.
The direction of the vector product is perpendicular to both vectors, $latex \vec{A}$ and $latex \vec{B}$. We can find its direction using the right-hand rule.
With our right hand, we rotate from the vector $latex \vec{A}$ to the direction of the vector $latex \vec{B}$. The fingers should point in the direction of the rotation:
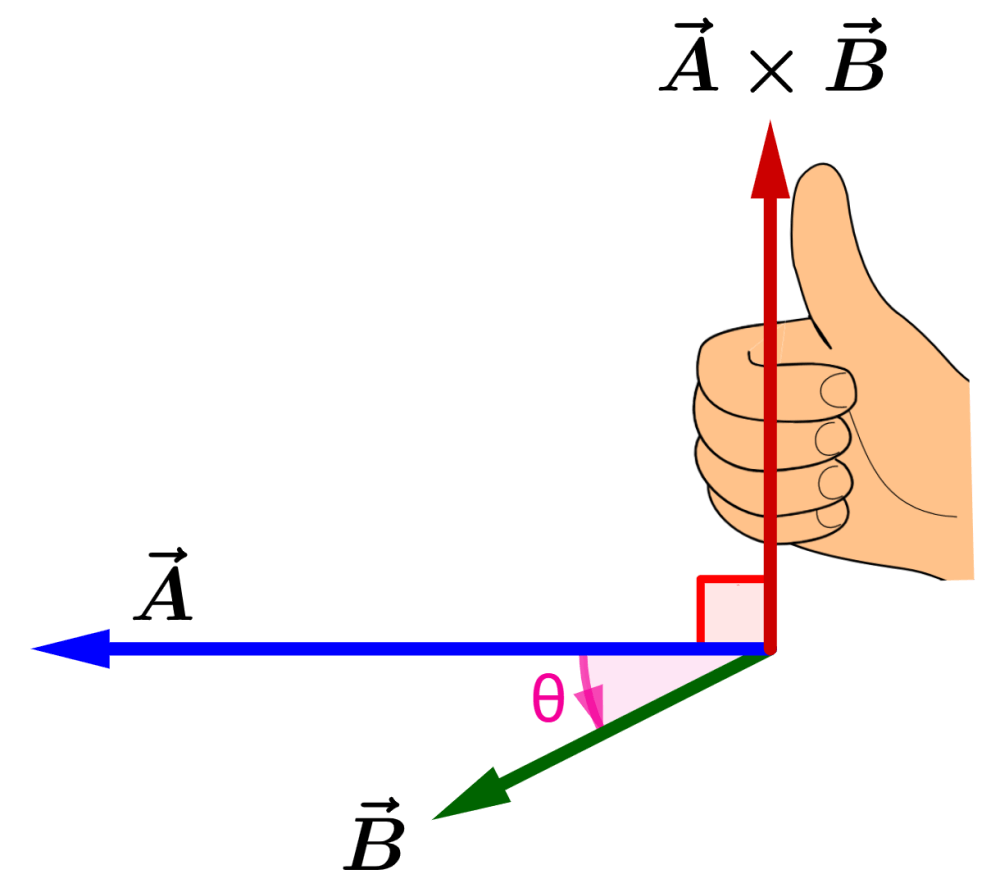
The thumb shows the direction of $latex \vec{A}\times \vec{B}$.
The direction of $latex \vec{B}\times \vec{A}$ is found by rotating from the vector $latex \vec{A}$ to the direction of the vector $latex \vec{B}$:
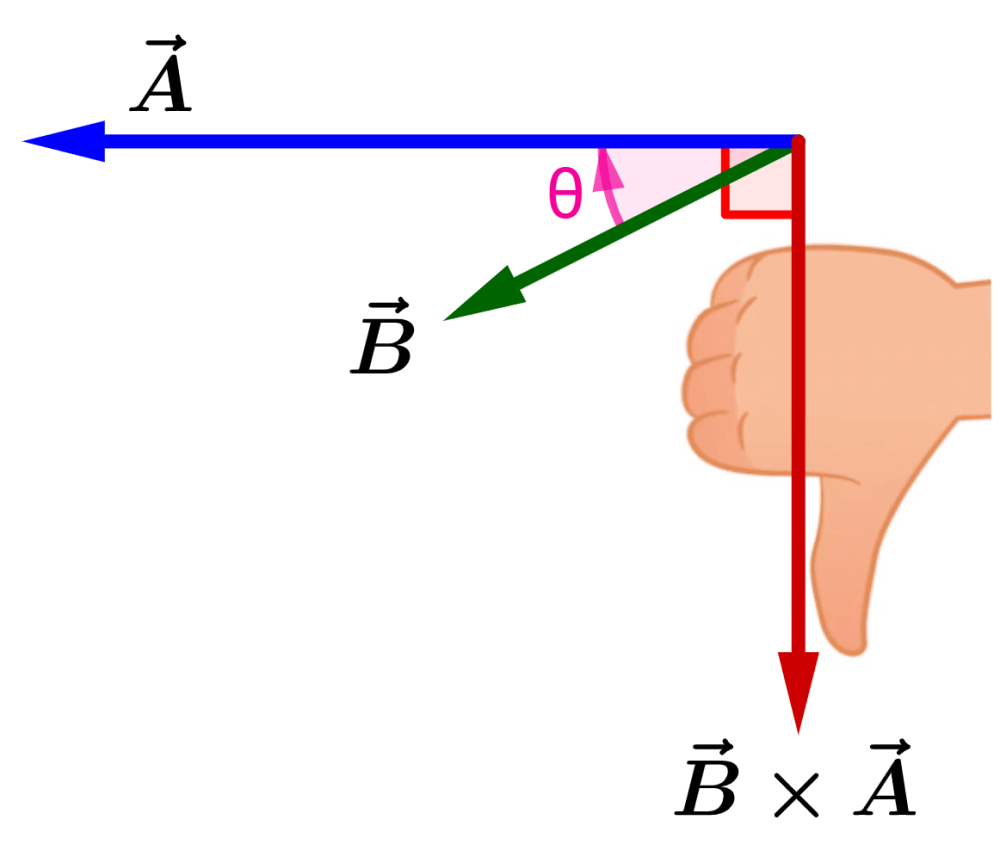
In the vector product, $latex \vec{B}\times \vec{A}$ is opposite to $latex \vec{A}\times \vec{B}$. That is, we have:
$latex \vec{A}\times \vec{B}=-\vec{B}\times \vec{A}$
Cross product of vectors using their components
When we know the components of the vectors, we can calculate the vector product $latex \vec{A} \cdot \vec{B}$ using the following formula:
$latex C_{x}=A_{y}B_{z}-A_{z}B_{y}$
$latex C_{y}=A_{z}B_{x}-A_{x}B_{z}$
$latex C_{z}=A_{x}B_{y}-A_{y}B_{x}$
You can read about the proofs of these formulas in this article: Formulas and properties of cross product of vectors.
EXAMPLE 1
A vector $latex \vec{A}$ has a magnitude of 8 units in the direction of $latex +x$. The vector $latex \vec{B}$ has a magnitude of 6 units and is in the $latex xy$ plane making an angle of 30° with the $latex +x$ axis.
What is the cross product $latex \vec{C}=\vec{A}\times \vec{B}$?
Solution
Since we know the magnitudes of the vectors and the angle between their directions, we can use the following formula to find the magnitude of the vector $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(8)(6)\sin(30^{\circ})$
$latex =24$
Now, we use the right-hand rule in the following diagram to find the direction of the vector $latex \vec{C}$:
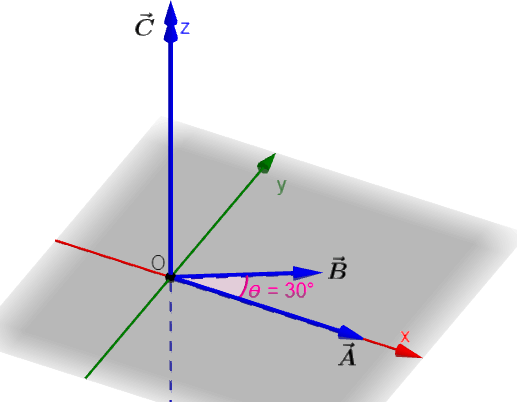
By the right-hand rule, the direction of $latex \vec{A}\times \vec{B}$ is along $latex +z$ or in the direction $latex \hat{k}$. Then,
$latex \vec{C}=\vec{A}\times \vec{B}=24\hat{k}$
EXAMPLE 2
If we have the vectors given below, what is the cross product $latex \vec{A} \times \vec{B}$?
$latex \vec{A} = 2 \hat{i} -3 \hat{j} +4 \hat{k}$
$latex \vec{B} = 1 \hat{i} +5 \hat{j} -2 \hat{k}$
Solution
Since we know the components of the vectors, we use the following formula:
$latex C_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex C_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex C_{z} =A_{x} B_{y} – A_{y} B_{x}$
where $latex \vec{C}=\vec{A} \times \vec{B}$. Then:
$latex \vec{A} \times \vec{B} = ((-3)(-2) – (4)(5))\hat{i} +( (4)(1)-(2)(-2))\hat{j} + ((2) (5) – (-3) (1))\hat{k}$
$latex \vec{A} \times \vec{B}=-14\hat{i} + 8\hat{j} + 13\hat{k}$
See also
Interested in learning more about vectors? Take a look at theses pages.
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
